ELEKTROmagnetism
- 1: PÕHIMÕISTED
- 1.1 ELEKTRIVOOL
- 1.2 PINGE
- 1.3 TAKISTUS
- 1.4 OHMI SEADUS
- ELEKTRIAHELATE LAHENDAMINE JA PÕHISEADUSED
- 1.5. COULOMB’I SEADUS
- 1.6. KIRCHHOFFI SEADUSED
- 1.7. JOULE-LENZI SEADUS
- 1.8. VÕIMSUS
- 2. ELEKTROMAGNETISM
- 1. ÕHUSÜDAMIKUGA MÄHISED
- 2. RAUDSÜDAMIKUGA MÄHISED
- 3. FERRIIT- VÕI PULBERSÜDAMIKUGA MÄHISED
- 4. TOROIDMÄHISED
- 5. VÕIMSUSINDUKTORID
- MÄHISTE KASUTUSVALDKONNAD JA FUNKTSIOONID
- SAGEDUSE SELEKTEERIMINE LC-RESONANTSAHELA ABIL
- SIGNAALI VÕIMENDAMINE
- A. VÕIMENDUSTRAFOD:
- B. SUURENENUD SIGNAALIKVALITEET:
- RESONANTSI LOOMINE RAADIOSAGEDUSTE JAOKS
- A. VASTUVÕTJATES:
- B. SAATJATES:
- KASUTAMINE RAADIO JA RAADIOSAGEDUSLIKES RAKENDUSTES
- 4. TRAFO PÕHIMÕTE JA MUTUAALNE INDUKTSIOON
- 5. ELEKTROMAGNETID (SOLENOIDID)
- LINEAARLIIKUMISEGA SOLENOID
- KAHE SUUNALISED LINEAARLIIKUMISEGA SOLENOIDID
- BISTABIILSED SOLENOID
- PÖÖRDLIIKUMISEGA SOLENOIDID
- HOIDESOLENOIDID EHK HOIDEMAGNETID
- OLULISED PARAMEETRID
- KOKKUVÕTE
- Induktiivpool
1: PÕHIMÕISTED
Selles peatükis käsitletakse elektrotehnika ja elektroonika kolme olulist põhimõistet: elektrivoolu, pinget ja takistust. Samuti käsitletakse Ohmi seadust, mis seob need kolm mõistet omavahel ja on aluseks elektriliste vooluringide analüüsile.
1.1 ELEKTRIVOOL
Definitsioon:
Elektrivool on laetud osakeste (peamiselt elektronide) liikumine juhtmes või muus juhtivas keskkonnas. Elektrivool tekib, kui laetud osakesed liiguvad ühes suunas, mida põhjustab pinge. Elektrivoolu tugevust mõõdetakse amprites (A), mis näitab, kui palju laengut (kulonites, C) läbib juhti teatud ajaühikus (sekundites, s).

Tähis ja ühik:
- Tähis: I
- Ühik: Amper (A)
Matemaatiline seos:
kus:
- I on voolutugevus, mõõdetakse amprites (A),
- Q on laeng, mõõdetakse kulonites (C),
- t on aeg, mille jooksul see laeng juhti läbib, mõõdetakse sekundites (s).
1.2 PINGE
Pinge on elektriväli, mis paneb laetud osakesed liikuma juhtmes. See tekib, kui juhtme kahe punkti vahel on potentsiaalne erinevus. Pinge mõõdetakse voltides (V) ja tähistatakse U või V. Matemaatiliselt seostub pinge tööga (W) ja laenguga (Q) järgmise valemiga:
Pinge valem:
Kus:
- U on pinge voltides (V),
- W on töö džaulides (J),
- Q on laeng kulonites (C).
Ilma pingeta ei saa elektrivool juhtmes liikuda, sest just pinge tekitab voolu. Mjau!
1.3 TAKISTUS
Definitsioon:
Takistus on omadus, mis piirab voolu läbimist juhtmes või komponendis. Takistus tekib seetõttu, et juhtme sees olevad aatomid takistavad elektronide liikumist. Takistust mõõdetakse oomides (Ω) ja see sõltub materjali tüübist, juhtme pikkusest ja ristlõike pindalast.
Tähis ja ühik:

- Tähis: R
- Ühik: Oom (Ω)
Matemaatiline seos:
kus:
- R on takistus, mõõdetakse oomides (Ω),
- U on pinge, mõõdetakse voltides (V),
- I on voolutugevus, mõõdetakse amprites (A).
Juhi takistuse arvutamine on oluline osa elektriahela analüüsist. Takistust mõõdetakse oomides (Ω) ja see sõltub juhi pikkusest, ristlõikepindalast, materjalist ning temperatuurist. Juhi takistust saab arvutada järgmise valemi abil:
TAKISTUSE VALEM:
Kus:
- R on juhi takistus (oomides, Ω),
- ρ (rho) on materjali eritakistus ehk spetsiifiline takistus (oom-meetrites, Ω·m),
- L on juhi pikkus (meetrites, m),
- A on juhi ristlõikepindala (ruutmeetrites, m²).
ERITAKISTUS (Ρ):
Eritakistus on materjali omadus ja see näitab, kui palju takistab materjal elektrivoolu liikumist. Eritakistus sõltub materjalist ja temperatuurist. Näiteks vask on hea juht ja selle eritakistus on väiksem kui raual või alumiiniumil.
RISTLÕIKEPINDALA (A):
Juhi ristlõikepindala on pindala, mis on risti voolu liikumise suunaga. Tavaliselt on juhtmed silindrilise kujuga, nii et ristlõikepindala saab arvutada valemiga:
Kus:
- r on juhi raadius (meetrites).
Kui juhi läbimõõt (d) on teada, siis:
NÄIDE:
Oletame, et teil on 10 meetri pikkune vaskjuhe, mille läbimõõt on 2 mm (0,002 m). Vaskjuhtme eritakistus on umbes 1,68 × 10⁻⁸ Ω·m.
- Arvutage ristlõikepindala:
- Arvutage takistus:
Selle valemi abil saate arvutada takistuse mis tahes juhtiva materjali puhul, kui materjali eritakistus ja juhi geomeetrilised omadused on teada.
1.4 OHMI SEADUS
Seaduse sõnastus:
Ohmi seadus seob omavahel pinge (U), voolutugevuse (I) ja takistuse (R) elektrilises vooluringis. Seaduse kohaselt on voolutugevus juhtmes võrdeline pinge suurusega ja pöördvõrdeline takistuse suurusega.
Matemaatiline väljend:
kus:
- I on voolutugevus (A),
- U on pinge (V),
- R on takistus (Ω).
Rakendused:
- Voolu arvutamine: Kui on teada pinge ja takistus, saab Ohmi seaduse abil arvutada voolutugevuse vooluringis.
- Pinge arvutamine: Kui on teada voolutugevus ja takistus, saab arvutada pinge.
- Takistuse arvutamine: Kui on teada pinge ja voolutugevus, saab arvutada takistuse.
Näide:
Oletame, et vooluringis on takisti, mille takistus on 4 Ω, ja sellele rakendatakse 12 V pinget. Voolutugevuse leidmiseks kasutame Ohmi seadust:
See tähendab, et voolutugevus juhis on 3 amprit.
Ohmi seadus on fundamentaalne tööriist elektriliste vooluringide analüüsis ja disainis, võimaldades inseneridel ja tehnikutel arvutada ja planeerida, kuidas erinevad elektrilised komponendid koos töötavad.
ELEKTRIAHELATE LAHENDAMINE JA PÕHISEADUSED
Selles peatükis käsitleme elektrotehnika olulisi põhiseadusi, nagu Coulomb’i seadus, Kirchhoffi seadused ja Joule-Lenzi seadus, mis on kriitilise tähtsusega elektriahelate analüüsimisel ja lahendamisel. Esitame need seadused üksikasjalikult koos näidetega, et selgitada, kuidas neid seadusi praktikas rakendada.
1.5. COULOMB’I SEADUS

Seaduse sõnastus:
Coulomb’i seadus kirjeldab jõudu, mis toimib kahe laetud keha vahel. Jõud on võrdeline laengute suurusega ja pöördvõrdeline nendevahelise kauguse ruuduga. Seda seadust kasutatakse laetud osakeste vahelise elektrilise jõu arvutamiseks.
Matemaatiline seos:
kus:
- F on jõud, mõõdetakse newtonites (N),
- k on Coulomb’i konstant
,
- q1 ja q2 on laengud kulonites (C),
- r on laengutevaheline kaugus meetrites (m).
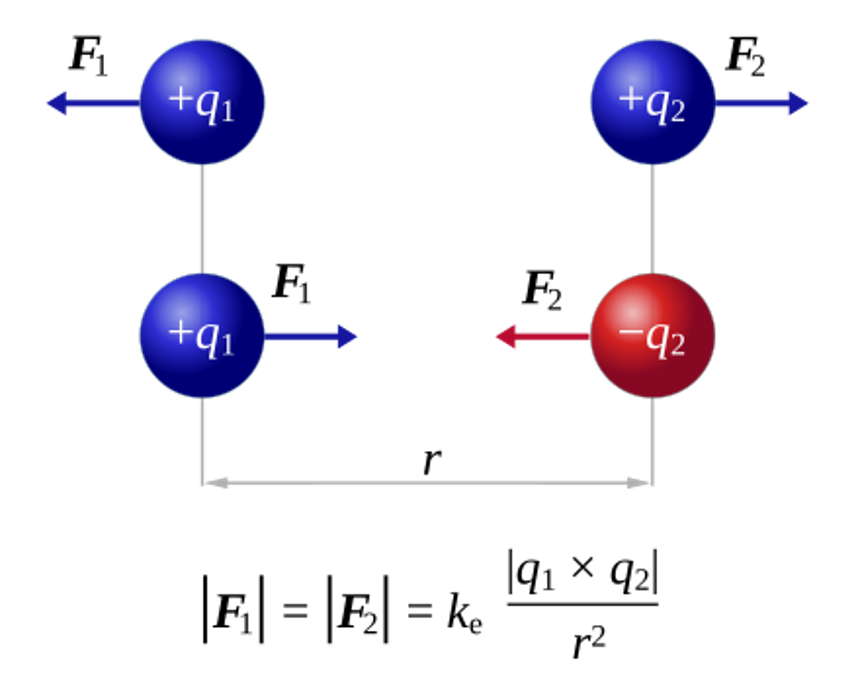
Näide:
Kaks punkti laengut,
, paiknevad 1 meetri kaugusel teineteisest. Leiame nende laengute vahelise jõu.
Tulemus on
,
mis tähendab, et jõud on tõmbav, kuna ühe laengu märgiks on positiivne ja teise oma negatiivne.
Rakendused:
- Coulomb’i seadust kasutatakse laetud kehade vaheliste jõudude arvutamiseks, näiteks füüsikas või inseneriteadustes, et arvutada elektromagnetiliste komponentide mõju.
1.6. KIRCHHOFFI SEADUSED
Kirchhoffi seadused on elektrivoolude ja pingete jaotumise kohta elektrivooluringides kehtivad kaks olulist reeglit. Need seadused aitavad lahendada keerukamaid vooluringe, kus on mitu hargnemist ja mitmesuguseid komponente.
KIRCHHOFFI VOOLUSEADUS (KVS)

Seaduse sõnastus:
Kirchhoffi vooluseadus (I seadus) ütleb, et voolude summa igas vooluringi hargnemiskohas on null. See tähendab, et kõikide sisenevate voolude summa peab olema võrdne väljuvate voolude summaga.
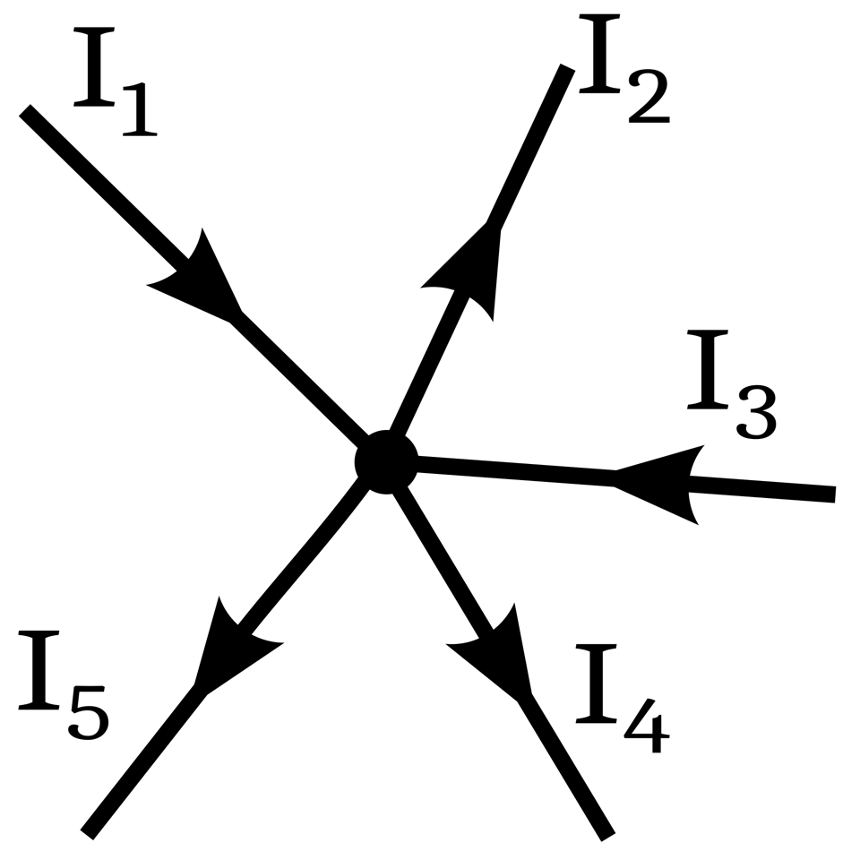
Matemaatiline seos:
Näide:
Vaadake vooluringi, kus vooluallikas jagab voolu kolmeks haruks. Hargnemiskohal on sisenev vool
ja väljuvad voolud on
.
Leiame kolmanda haru voolu (I_4).
Seega on kolmanda haru vool
.
Rakendused:
- Kirchhoffi vooluseadust kasutatakse hargnenud vooluringide arvutamiseks, näiteks vooluahelate tasakaalu ja koormusjaotuse leidmisel.
ÜLESANNE – KIRCHHOFFI I SEADUS
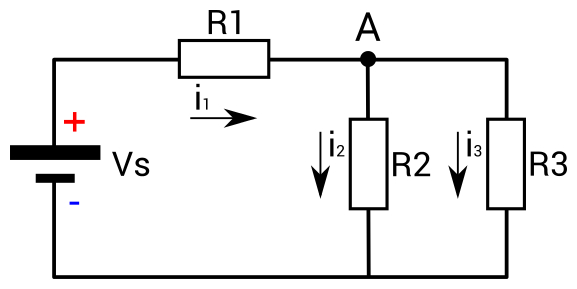
Olgu ülesandeks leida joonisel toodud ahela voolutugevused 






Vool läbib ahelat kahte kontuuri pidi – läbi takistite 




Kirchhoffi teise seaduse kohaselt on kontuuri läbivate pingelangude summa võrdne nulliga. Et antud skeemis on pingeallikast lähtuvalt kaks kontuuri, saame kirjutada:

Koostame võrrandisüsteemi

Seda võrrandisüsteemi lahendades saame 
Kontrollime vastavust Kirchhoffi esimesele seadusele:
Ülesanne võetud: https://et.wikipedia.org/wiki/Kirchhoffi_seadused
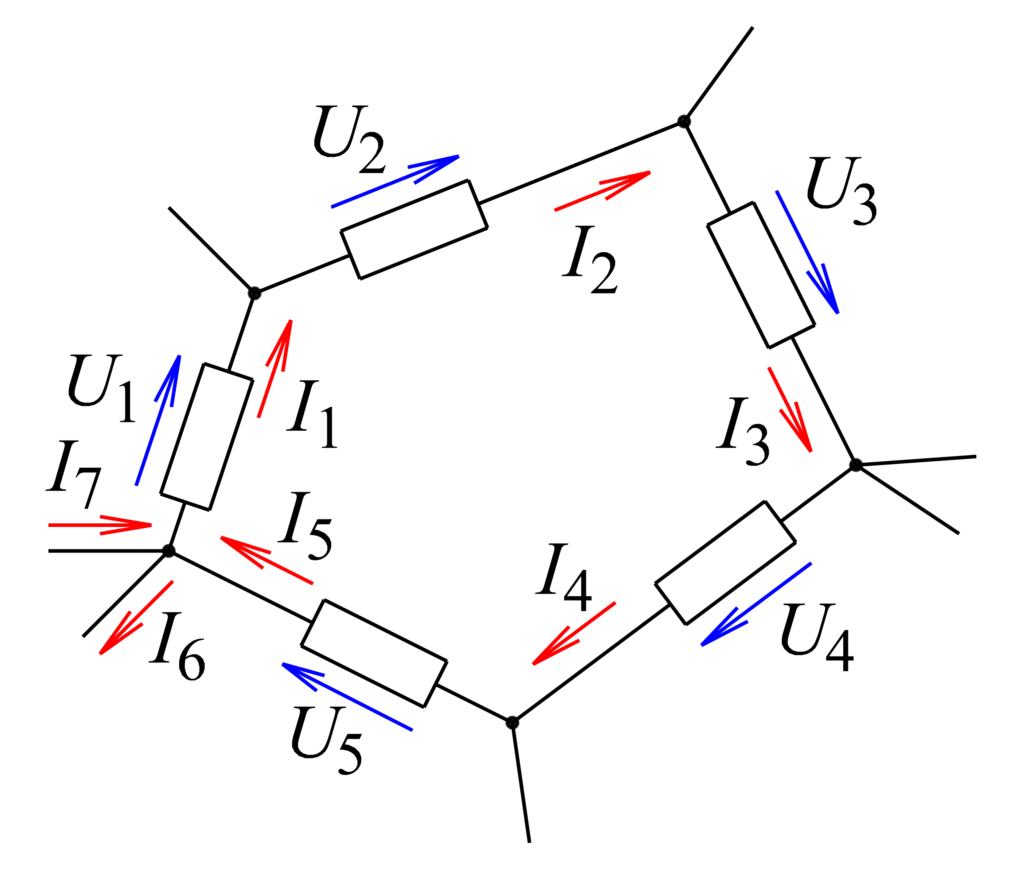
KIRCHHOFFI PINGESEADUS (KPS)
Seaduse sõnastus:
Kirchhoffi pingeseadus (II seadus) ütleb, et suletud vooluringis on kõigi pingelangude summa võrdne pingeallikate summaga. See tähendab, et vooluringi igas suletud silmuses peab kogu pingete summa olema null.
Matemaatiline seos:
Näide:
Vaatame suletud vooluringi, kus pingeallikas annab ja vooluringis on kaks takistit:
Leiame voolu vooluringis.
Kasutame Ohmi seadust:
- Pingeallikas annab kokku
.
- Pingelangud on:
.
Vooluringis peab pinge olema tasakaalus:
Seega on vool vooluringis .
Rakendused:
- Kirchhoffi pingeseadust kasutatakse vooluringide analüüsimiseks ja pingejaotuste leidmiseks keerukates elektrivõrkudes, näiteks arvuti toiteplokkides ja auto elektrisüsteemides.
ÜLESANNE KIRCHHOFFI II SEADUS
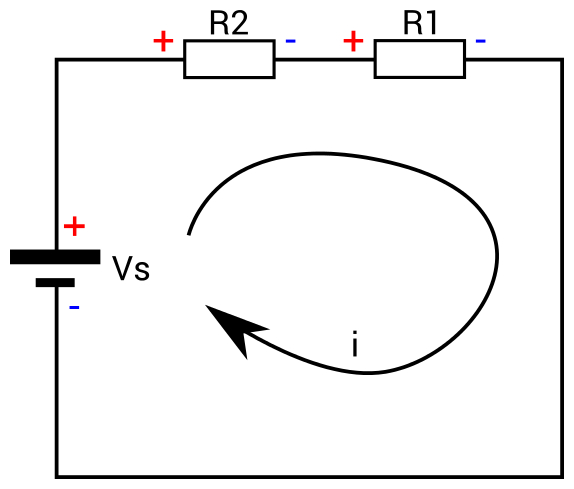
Olgu ülesandeks leida pingelangud joonisel toodud skeemi takistitel 




Edasi lepitakse kokku, et takistil tekib voolu liikumise suunas pingelang, ehk takisti ühel pool (pingeallika positiivsele klemmile lähemal) on pinge kõrgem kui teisel. Sama kokkulepe kehtib kõikidele kontuuris olevatele takistitele. Jällegi, seadus töötab ka vastupidise kokkuleppe korral.
Nüüd on ülesande lahendamiseks kõik suurused teada ja kokkulepped joonisele 2 kantud. Lähtudes definitsioonist 

Kirjutame eelmise seose lähtudes Oomi seadusest järgmiselt
Selle võrrandi lahendamiseks on kõik suurused teada, seega
Teades kontuuri läbivat voolu, saame arvutada pingelangud:

Kontrollime vastavust Kirchhoffi teisele seadusele: 
Ülesanne võetud: https://et.wikipedia.org/wiki/Kirchhoffi_seadused
1.7. JOULE-LENZI SEADUS

Seaduse sõnastus:
Joule-Lenzi seadus ütleb, et elektrivoolu käigus arenev soojusenergia on võrdeline voolutugevuse ruudu, takistuse ja ajaga, mille jooksul vool läbi takisti läbib.
Matemaatiline seos:
kus:
- Q on soojushulk, mõõdetakse džaulides (J),
- I on voolutugevus amprites (A),
- R on takistus oomides
,
- t on aeg sekundites (s).
Näide:
Oletame, et elektriline soojenduskeha töötab voolutugevusega , ja selle takistus on
. Arvutame, kui palju soojust eraldub (60) sekundi jooksul.
Seega eraldub soojenduskehas (15 000) džauli soojust.
Rakendused:
- Joule-Lenzi seadust kasutatakse elektriliste kütteseadmete disainimisel ja soojuskao arvutamisel elektrijuhtmetes ning seadmete ohutuse tagamisel.
See peatükk annab ülevaate Coulomb’i, Kirchhoffi ja Joule-Lenzi seadustest ning selgitab, kuidas neid kasutada elektrivooluringide analüüsimisel ja lahendamisel. Seaduste rakenduste mõistmine aitab õpilastel lahendada praktilisi ülesandeid ja töötada välja tõhusaid elektriahelaid.
1.8. VÕIMSUS
Võimsuse arvutamine alalisvoolu (DC) ja vahelduvvoolu (AC) korral toimub erinevate meetoditega, kuna nende voolutüüpide omadused on erinevad. Allpool on selgitatud, kuidas võimsust arvutada mõlemas voolutüübis.

ALALISVOOL (DC)
Alalisvoolus on pinge ja vool konstantne, seega võimsuse arvutamine on suhteliselt lihtne.
VALEM:
Kus:
- P on võimsus (vattides, W),
- U on pinge (voldis, V),
- I on voolutugevus (amprites, A).
NÄIDE:
Kui teil on alalisvooluahel, kus pinge on 12 V ja voolutugevus 2 A, siis võimsus on:
2. ELEKTROMAGNETISM
Elektromagnetism on füüsika haru, mis uurib elektrivoolu ja magnetvälja omavahelist seost. See on elektrotehnika ja elektroonika keskne osa, sest paljud seadmed ja tehnoloogiad põhinevad elektromagnetilistel põhimõtetel. Selles peatükis käsitleme magnetvälja ja elektrivoolu vahelist suhet, sealhulgas Lorentzi jõudu ja elektromagnetilist induktsiooni, ning arutame transformaatorite tööpõhimõtteid ja nende rakendusi.

3.1 MAGNETVÄLJA JA ELEKTRIVOOLU SUHE
Magnetväli ja elektrivool:
Kui elektrivool liigub läbi juhi (näiteks traadi), tekitab see enda ümber magnetvälja. See magnetväli ümbritseb juhti kontsentriliste rõngastena, mille suund sõltub voolu suunast. Seda nähtust kirjeldab Ampère’i seadus.
Lorentzi jõud:
Lorentzi jõud on jõud, mida magnetväli avaldab liikuvale laetud osakesele, näiteks elektronile. Kui laetud osake liigub läbi magnetvälja, mõjub sellele jõud, mis on risti nii magnetvälja suuna kui ka osakese liikumise suunaga. Lorentzi jõud on oluline mõiste elektromagnetilistes seadmetes, nagu elektrimootorid ja generaatorid.
Matemaatiline seos:
Lorentzi jõud (F) on määratud järgmise valemiga:
kus:
- F on jõud, mõõdetakse newtonites (N),
- q on osakese laeng, mõõdetakse kulonites (C),
- v on osakese kiirus, mõõdetakse meetrites sekundis (m/s),
- B on magnetvälja induktsioon, mõõdetakse teslades (T),
- × sümbol tähistab vektorkorrutist, mis tähendab, et jõud on risti nii osakese liikumise kui ka magnetvälja suunaga.
Elektromagnetiline induktsioon:
Elektromagnetiline induktsioon on protsess, mille käigus muutuva magnetvälja mõjul tekib juhtmes elektrivool. Seda nähtust kirjeldab Faraday seadus, mis ütleb, et ajas muutuv magnetväli tekitab elektrivälja, mis indutseerib elektrivoolu juhtmes.
Matemaatiline seos:
Faraday elektromagnetilise induktsiooni seadus:
kus:
- on indutseeritud elektromotoorjõud (emj), mõõdetakse voltides (V),
- on magnetvoog, mõõdetakse veebrites
,
- t on aeg, mõõdetakse sekundites (s).
Magnetvoog on defineeritud kui magnetvälja tugevuse (B) ja pindala (A), mille kaudu väli läbib, korrutis:
kus:
- B on magnetvälja induktsioon, mõõdetakse teslades (T),
- A on pindala, mille kaudu magnetväli läbib, mõõdetakse ruutmeetrites (m²),
- on nurk magnetvälja ja pinna normaali vahel.
Parema ja vasaku käe reeglid on visuaalsed meetodid elektri- ja magnetväljade mõjude suuna määramiseks. Need on olulised elektromagnetismi mõistmiseks ja rakendamiseks erinevates tehnoloogiates.
ÕPPEMATERJAL GÜMNAASIUMI FÜÜSIKAST: PAREMA JA VASAKU KÄE REEGLID
1. SISSEJUHATUS
- Eesmärk: Tutvustada parema ja vasaku käe reeglite põhimõtteid ja nende rakendusi elektromagnetismis.
- Taust: Elektrivool läbi juhtme tekitab selle ümber magnetvälja. Laetud osakese liikumine magnetväljas tekitab jõu, mis mõjutab osakese trajektoori.
2. PAREMA KÄE REEGEL
- Kirjeldus: Kasutatakse magnetvälja suuna määramiseks, mis on tekitatud elektrivoolu poolt, või jõu suuna määramiseks, mis mõjub laetud osakesele.
- Praktika:
- Magnetvälja suund: Siruta parema käe sõrmed välja ja suuna pöial voolu suunas läbi juhtme. Ülejäänud sõrmed näitavad magnetvälja suunda ümber juhtme.
- Jõud laetud osakesele: Kui positiiivne laeng liigub magnetväljas, suuna pöial voolu (liikumise) suunas, peopesa magnetvälja suunas ja sõrmed näitavad jõu suunda.
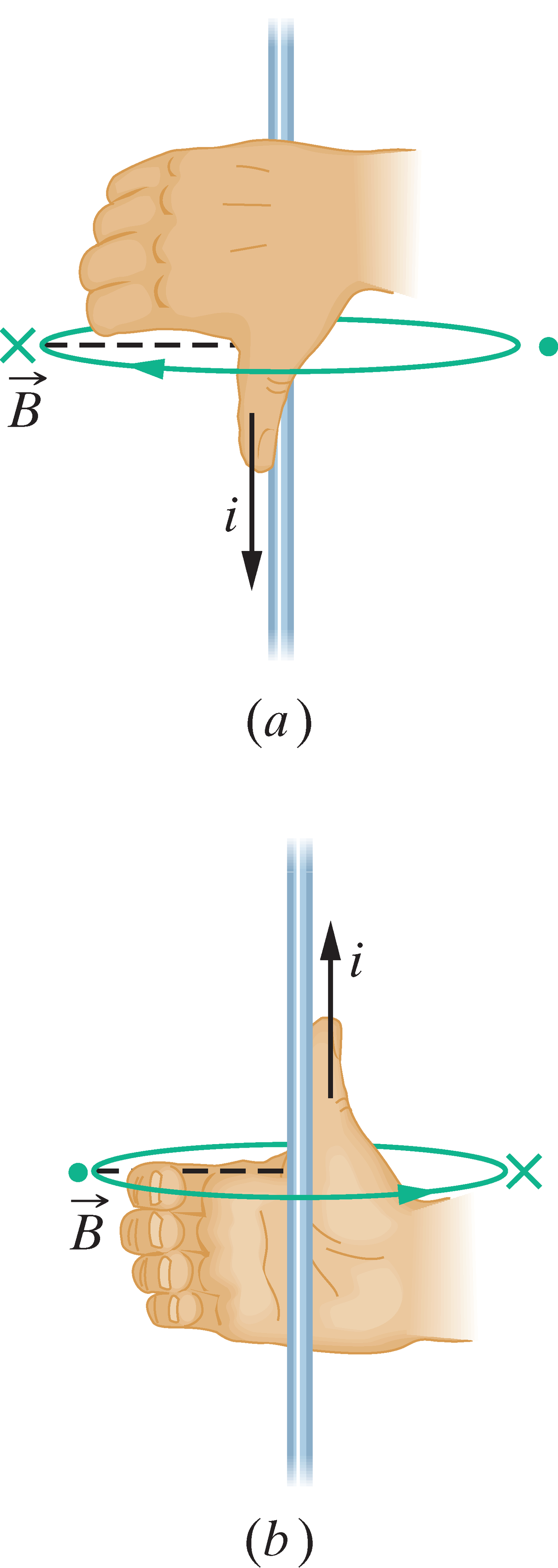
Parema käe reegel annab vooluga juhtme magnetvälja suuna
Parema käe reegel annab vooluga juhtme magnetvälja suuna. (a) Joonisel 29-2 kujutatud situatsioon külgvaates. Magnetväli →B suvalises juhtmest vasakul asetsevas punktis on risti radiaalse punktiirjoonega ja suunatud lehekülje tasandi sisse sõrmedega näidatud suunas, mida näitab ka tähis ×. (b) Kui muuta voolu suund vastupidiseks, siis on magnetväli →B suvalises juhtmest vasakul asetsevas punktis ikka suunatud risti radiaalse punktiirjoonega, kuid nüüd on see suunaga lehekülje tasandist välja, mida näitab ka tähis. (https://opik4.fyysika.ee/index.php/book/section/13308)
3. VASAKU KÄE REEGEL
- Kirjeldus: Kasutatakse mootoriefekti kirjeldamiseks, kus elektrivool ja magnetväli koosmõjul tekitavad jõu.
- Praktika:
- Aseta vasak käsi nii, et sõrmed osutavad magnetvälja suunas ja peopesa voolu suunas. Pöial näitab seejärel jõu suunda, mis mõjub juhtmele või laetud osakesele.
Joonisel on kujutatud kahte magnetit ja nende vahele asetatud vooluga juhtmelõiku. Veendu, et juhtmelõigule mõjuv magnetjõud on just selline, nagu joonisel kujutatud.
Lahendus
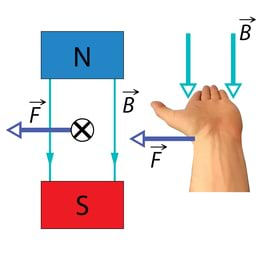
Joonisel on kujutatud ühe magneti põhjapoolus ja teise magneti lõunapoolus. Magnetvälja jõujoonte suund on järelikult ülevalt alla (põhjapooluselt lõunapoolusele). Juhtmelõik on magnetväljaga risti. Voolu suund on tähistatud ristiga juhtme ristlõik (https://opik4.fyysika.ee/index.php/book/section/13308).
4. RAKENDUSED JA NÄITED
- Elektrimootorid: Selgitatakse, kuidas elektrimootorid kasutavad vasaku käe reeglit pöörlemisjõu tekitamiseks.
- Generaatorid: Tutvustatakse, kuidas generaatorid kasutavad parema käe reeglit elektri tootmiseks mehaanilisest liikumisest.
5. HARJUTUSED JA KATSETUSED
- Virtuaalne simulatsioon: Kasutajad saavad virtuaalselt simuleerida erinevaid stsenaariume, kus rakendatakse mõlemat käe reeglit.
- Füüsilised katsetused: Juhendid lihtsate katsete jaoks, mida saab läbi viia kodus või klassiruumis, et demonstreerida käe reeglite mõjusid.
6. KOKKUVÕTE
- Ülevaade õpitu olulisusest ja kuidas parema ja vasaku käe reegleid saab rakendada praktilistes olukordades tehnoloogia ja inseneriteaduste valdkonnas.
Selline struktureeritud lähenemine aitab õppijatel paremini mõista ja meelde jätta parema ja vasaku käe reeglite teoreetilisi aluseid ning praktikat.
3.2 TRANSFORMAATORID JA NENDE TÖÖPÕHIMÕTE
Transformaatorite tööpõhimõte:
Trafo on seade, mis muundab vahelduvvoolu pinge ühest väärtusest teise, kasutades elektromagnetilise induktsiooni põhimõtet. Trafo koosneb kahest või enamast mähisest (esmane ja sekundaarne mähis), mis on paigutatud ümber ühise raudtuuma. Kui esmasele mähisele rakendatakse vahelduvvool, tekitab see muutuva magnetvälja, mis indutseerib pinge sekundaarse mähise kaudu.
Põhikomponendid:
- Primaarne mähis: Mähis, millele rakendatakse esialgne pinge.
- Sekundaarne mähis: Mähis, milles indutseeritakse pinge läbi elektromagnetilise induktsiooni.
- Raudtuum: Suunab magnetvoo läbi mähiste, suurendades induktsiooni efektiivsust.
Matemaatiline seos:
Transformaatori tööpõhimõtet kirjeldab järgnev valem, mis seob primaarse ja sekundaarse mähise pinged ning pöördeteguri:
kus:
- on primaarse mähise pinge, mõõdetakse voltides
,
- on sekundaarse mähise pinge, mõõdetakse voltides
,
- on primaarse mähise keerdude arv,
- on sekundaarse mähise keerdude arv.
See tähendab, et pinge suhe on võrdeline mähiste keerdude arvuga. Kui sekundaarse mähise keerdude arv on suurem kui primaarse mähise oma, siis trafo suurendab pinget; vastasel juhul vähendab pinget.
Trafo tüübid:
- Tõstetrafo (Step-up transformer):
- Suurendab pinget esmase mähise madalast pingest kõrgemale pingele.
- Kasutatakse elektrienergia ülekandmisel pikkade vahemaade taha.
- Langetustrafo (Step-down transformer):
- Vähendab pinget kõrgemalt väärtuselt madalamale.
- Kasutatakse kodumajapidamistes ja tööstuses, et viia kõrge pinge elektrivõrgust madalamale kasutamiseks ohutule tasemele.
- Isolatsioonitrafo:
- Ülekanne toimub sama pingetaseme juures, kuid eraldab vooluahelaid elektriliselt.
- Kasutatakse ohutuse tagamiseks ja häirete vähendamiseks.
Kasutusalad:
- Elektrienergia ülekandmine: Trafo suurendab pinge elektrijaamades, et vähendada kaod elektrienergia ülekandmisel pikkade vahemaade taha. Sihtkohas langetatakse pinge tagasi tarbimiseks sobivale tasemele.
- Elektroonikaseadmed: Paljud elektroonikaseadmed kasutavad transformaatoreid toiteallikatena, et muundada vahelduvvoolu pinge vajalikule tasemele.
- Tööstuslikud rakendused: Trafo võimaldab juhtida erinevaid pingeid tööstuslikes seadmetes ja masinates.
Elektromagnetism on laiapõhjaline teadusharu, mis hõlmab elektri ja magnetismi vastastikmõjusid. Lorentzi jõud ja elektromagnetiline induktsioon on kaks peamist fenomeni, mis juhivad elektrivoolu ja magnetvälja vahelist seost. Trafo on praktiline seade, mis kasutab neid põhimõtteid elektrienergia tõhusaks ülekandmiseks ja muundamiseks. Nende kontseptsioonide mõistmine on oluline elektrotehnika ja elektroonika alal edasijõudmiseks ja rakenduste arendamiseks.
INDUKTIIVPOOL (MÄHIS)
Komponendid mitmesugustes elektroonikaseadmetes, alates lihtsatest toiteallikatest kuni keeruliste andmetöötlussüsteemideni.

- Sümbol:

- Kirjeldus: Induktiivpool salvestab energiat magnetväljas ja seda kasutatakse sagedusfiltrites, energia salvestamisel ja mujal.
- Tähis: L
- Ühik: Henry (H)
Induktiivsus on füüsikaline suurus, mis iseloomustab induktiivpooli (mähise) võimet tekitada elektromotoorjõudu (pinget) voolu muutumise korral. Induktiivsuse ühik on henri (H).
INDUKTIIVSUS SIRGE MÄHISE JAOKS:
Induktiivsuse saab sirge mähise jaoks arvutada järgmise valemi abil:
Kus:
on induktiivsus
,
on vaakumi magnetiline läbitavus
,
on mähise südamiku suhteline magnetiline läbitavus (dielektrilise materjali omadus),
on mähise keerude arv,
on mähise ristlõike pindala
,
on mähise pikkus
.
2. ELEKTROMAGNETILINE INDUKTSIOON (FARADAY SEADUS):
Kui voolu muutumine ajas tekitab mähises pinge, siis selle pinge ( \varepsilon ) on antud valemiga:
Kus:
on induktiivpooli tekitatud pinge
,
on induktiivsus
,
on voolu muutumise kiirus ajas
.
3. INDUKTIIVNE REAKTANTS VAHELDUVVOOLU PUHUL:
Vahelduvvoolu (AC) puhul takistab induktiivpool voolu, mis tekib selle magnetväljas, ja see takistus on tuntud kui induktiivne reaktants ( X_L ):
Kus:
on induktiivne reaktants
,
on vahelduvvoolu sagedus
,
on induktiivsus
.
Mida suurem on sagedus või induktiivsus, seda suurem on induktiivne reaktants, mis piirab voolu läbimist mähisest.
4. ENERGIA INDUKTIIVPOOLIS:
Induktiivpooli magnetvälja salvestatud energia ( E ) on antud valemiga:
Kus:
on energia
,
on induktiivsus
,
on vool
.
5. INDUKTIIVPOOLI FAASINIHE VAHELDUVVOOLU PUHUL:
Vahelduvvoolu (AC) korral tekitab induktiivpool voolu ja pinge vahele faasinihke, kus pinge on voolu faasist 90 kraadi ees. See tähendab, et maksimaalne pinge saavutatakse siis, kui vool hakkab muutuma.
Need on peamised valemid, mis käsitlevad induktiivsust ja induktiivpoolide käitumist vooluahelates.
INDUKTIIVPOOLI (MÄHISE) TÖÖPÕHIMÕTE JA LIIGITUS
TÖÖPÕHIMÕTE
Induktiivpool, mida sageli nimetatakse ka mähiseks, on elektrotehniline komponent, mille peamine funktsioon on salvestada energiat magnetvälja kujul, kui vool läbib seda. Mähis koosneb tavaliselt isoleeritud traadist, mis on keritud silindrikujuliselt või spiraalina ümber tuuma, mis võib olla õhu või ferromagnetilise materjaliga (nt raud). Induktiivpoolsuse (L) suurust mõõdetakse henrites (H).
Kui vool liigub läbi mähise, tekitab see selle ümber magnetvälja. Mähise elektritakistus on minimaalne, kuid selle induktiivtakistus takistab voolu muutusi ahelas. Mida kiirem on voolu muutus, seda suurem on vastutekkiv induktiivne pingelang. Seda nähtust nimetatakse induktsiooniks ja selle kaudu hoiab induktiivpool energia salvestamist magnetväljas.
INDUKTIIVPOOLI PÕHIOMADUSED:
- Induktiivsus (L) – määrab, kui tõhusalt mähis salvestab energiat magnetvälja kujul. See sõltub mähise traadi keerdude arvust, keerdude tihedusest, südamiku materjalist ja südamiku geomeetriast.
- Eneseinduktsioon – kui voolu muutus mähises tekitab selles endas pinge, mis püüab vastu seista voolu muutusele.
- Mutuaalne induktsioon – esineb kahe või enama mähise vahel, kus ühe mähise magnetväli indutseerib teises mähises pinge (nt trafo tööpõhimõte).
INDUKTIIVPOOLI LIIGITUS
Mähised liigitatakse mitmel viisil, sõltuvalt nende konstruktsioonist, funktsioonist ja kasutusvaldkonnast.
1. ÕHUSÜDAMIKUGA MÄHISED
Need on mähised, millel ei ole magnetilist südamikku – traadi keerdude vahel on lihtsalt õhk või muu mitte-magnetiline aine. Sellised mähised on lihtsad ja töökindlad, kuid nende induktiivsus on madal. Neid kasutatakse sageli raadio- ja kõrgsagedusrakendustes, kus on oluline vältida südamiku kaod.
- Tunnused: Madal induktiivsus, sobib kõrgetele sagedustele.
- Tüüpiline kasutus: Raadiovastuvõtjad, antennide mähised.
2. RAUDSÜDAMIKUGA MÄHISED
Selliste mähiste puhul on traadikeerdude sees ferromagnetiline südamik (näiteks raud või feriit), mis suurendab mähise induktiivsust, kuna südamik keskendab ja tugevdab magnetvälja. Raudsüdamikuga mähiseid kasutatakse peamiselt madalsagedusrakendustes ja kohtades, kus on vaja suurt induktiivsust.
- Tunnused: Suurem induktiivsus võrreldes õhusüdamikuga mähistega, kuid südamiku materjal võib tekitada kaotusi (nt hüstereesikaod ja pöörisvoolud).
- Tüüpiline kasutus: Võimsusmuundurid, trafod, elektromagnetid.
3. FERRIIT- VÕI PULBERSÜDAMIKUGA MÄHISED
Ferriit- ja pulbersüdamikuga mähised on spetsiaalselt loodud töötama kõrgetel sagedustel, pakkudes paremat jõudlust ja väiksemaid kaotusi võrreldes raudsüdamikuga mähistega. Ferriitmaterjal on mittejuhtiv ja suudab vältida pöörisvoolukadusid, mis esinevad kõrgsageduslikes rakendustes.
- Tunnused: Kõrgsageduste jaoks sobivad, väiksemad kaod ja suurem efektiivsus.
- Tüüpiline kasutus: Raadiosagedusmuundurid, filtrid, trafod.
4. TOROIDMÄHISED
Toroidmähised on spetsiaalse kujuga mähised, kus traat on keritud rõngakujulise (toroidse) südamiku ümber. Toroidmähised pakuvad paremat magnetvälja suunamist ja väiksemat kiirgust väljapoole mähist, vähendades elektromagnetilisi häireid (EMI).
- Tunnused: Kompaktne ja tõhus magnetvälja suunamine, väiksemad lekkeväljadel põhinevad kaod.
- Tüüpiline kasutus: Võimsustrafod, raadiosagedusfiltrid.
5. VÕIMSUSINDUKTORID
Võimsusinduktorid on suure võimsustaluvusega mähised, mis on mõeldud töötama kõrge vooluga rakendustes, kus on vaja energiat salvestada ja seejärel kiiresti vabastada. Tavaliselt kasutatakse neid toiteahelates ja muundurites.
- Tunnused: Kõrge voolutaluvus, madal takistus.
- Tüüpiline kasutus: SMPS (Switch Mode Power Supplies), DC-DC muundurid.
MÄHISTE KASUTUSVALDKONNAD JA FUNKTSIOONID
Mähiseid kasutatakse laialdaselt erinevates elektrotehnilistes rakendustes, alates energiasalvestusest kuni signaalide filtreerimiseni. Peamised funktsioonid ja kasutusvaldkonnad on järgmised:
1. ENERGIA SALVESTAMINE
Mähis salvestab energiat magnetvälja kujul, kui vool läbib seda. Seda energiat saab hiljem vabastada, kui vool väheneb või suunatakse teise vooluahelasse. See omadus on eriti oluline võimsusahelates, näiteks lülitusmuundurites ja pingeregulaatorites.
Mähise energia salvestamise põhimõte põhineb sellel, et kui vool läbib mähist, siis tekib selle ümber magnetväli. Mähis suudab salvestada energiat selles magnetväljas seni, kuni vool läbib mähist. Kui vool hakkab vähenema või katkeb, siis see magnetväli hakkab kokku kukkuma ja mähisesse tekib pingelang, mis suunab energia tagasi vooluringi.
See omadus on eriti kasulik ja oluline võimsusahelates, näiteks:
- Lülitusmuundurites: Mähised aitavad muuta pinget efektiivselt. Kui muundatakse näiteks alalisvoolu madalast pingest kõrgeks või vastupidi, kasutatakse mähiseid energia ajutiseks salvestamiseks ja vabastamiseks.
- Pingeregulaatorites: Mähised aitavad stabiliseerida voolu ja pinget. Kui süsteemis on voolu- või pingekõikumisi, siis mähise kaudu on võimalik säilitada stabiilsus, kuna ta suudab ajutiselt energiat salvestada ja seejärel vajadusel vabastada, hoides süsteemi töö stabiilsena.
Kokkuvõttes toimib mähis energiapuhvrina, mis võimaldab ajutiselt talletada energiat magnetvälja kujul ning seejärel sujuvalt vabastada, kui seda vajatakse vooluringis, aidates seeläbi stabiliseerida ja juhtida vooluringi tööd.
2. FILTREERIMINE JA SILUMINE
Mähised koos kondensaatoritega moodustavad LC-filtrid, mis filtreerivad välja soovimatud sagedused signaalist. Näiteks toiteallikates kasutatakse mähiseid pinge kõikumiste tasandamiseks ja müra vähendamiseks.
Filtreerimine ja silumine mähiste ja kondensaatorite abil toimib nii, et nad suudavad koos töötades kõrvaldada või vähendada soovimatuid sagedusi ja pinge kõikumisi elektrisüsteemis. See omadus on väga oluline, eriti toiteallikates ja elektroonikaseadmetes.
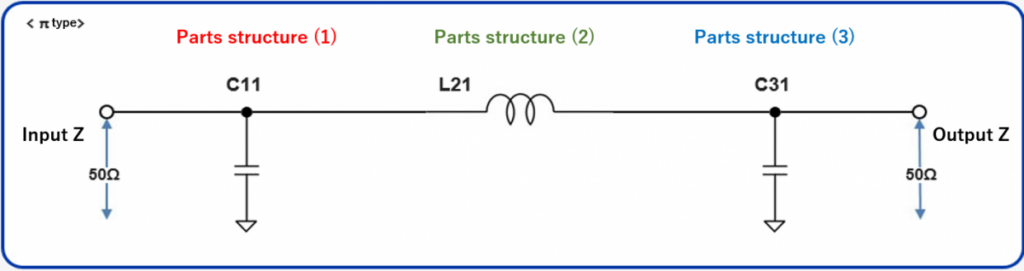
LC-FILTRID
- LC-filtrid koosnevad mähisest (L) ja kondensaatorist (C). Need komponendid töötavad koos, et blokeerida teatud sagedused ja lasta teised läbi. LC-filtrid filtreerivad välja soovimatud kõrgsageduslikud häired või müra signaalist, säilitades samal ajal kasuliku signaali.
- Mähis (L) takistab kõrgsageduslike signaalide läbimist, samal ajal kui madalsageduslikud signaalid liiguvad mähisest vabalt läbi.
- Kondensaator (C) toimib vastupidi – see laseb kõrgsageduslikud signaalid läbi, aga blokeerib madalsageduslikud signaalid.
Kombineeritult suudavad LC-filtrid eemaldada soovimatud sagedused ja hoida vajalikud signaalid puhtad.
PINGE KÕIKUMISTE TASANDAMINE JA MÜRA VÄHENDAMINE
- Toiteallikates on mähised kasutusel pinge ja voolu silumiseks ehk kõikumiste tasandamiseks. Elektrivõrgus või vooluallikas võib esineda müra või järske kõikumisi (nt lülitusmüra). Mähised aitavad neid kõikumisi sujuvamaks muuta, kuna nad salvestavad ja vabastavad energiat järk-järgult. See aitab vältida pinge järske muutusi ja hoida süsteemi stabiilsena. Näiteks toiteahelas aitavad mähised ja kondensaatorid koos vähendada kõrgsageduslikku müra, mis võib tekkida lülitusahelate tõttu, ning tagada stabiilse ja puhta pinge toidetavatele komponentidele.
LC-filtrid koosnevad induktiivpoolist (L) ja kondensaatorist (C) ning neid kasutatakse elektriliste signaalide filtreerimiseks teatud sageduste blokeerimiseks või lubamiseks. LC-filtrid on olulised elektroonikaseadmetes, nagu võimendid, raadiovastuvõtjad ja toiteallikad, kuna need suudavad puhastada signaale ja stabiliseerida süsteeme.
LC-FILTRITE PEAMISED TÜÜBID:
- Madalsagedusfilter (Low-pass filter):
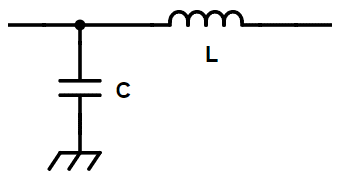
- Funktsioon: Laseb läbi madalad sagedused ja summutab kõrged sagedused.
- Kasutus: Kasutatakse sagedusvahemikus, kus madalsageduslik signaal peab läbima, kuid kõrgsageduslik müra tuleb blokeerida. Näiteks toiteallikates müra eemaldamiseks või helisüsteemides madalsageduslike komponentide edastamiseks.
- Ehitus: Tavaliselt koosneb induktiivpoolist ja kondensaatorist, kus induktiivpool on ühendatud signaaliteega ja kondensaator maaga, mis loob võime kõrgsagedusi summutada.
- Tüüpiline rakendus: Signaalide filtreerimine toiteahelates (nt vahelduvvoolu komponentide eemaldamine alalisvoolust), helisüsteemid, helivõimendid.
- Kõrgsagedusfilter (High-pass filter):
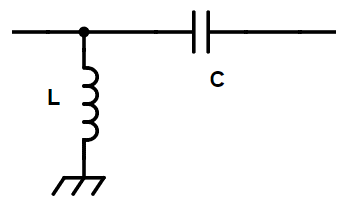
- Funktsioon: Laseb läbi kõrged sagedused ja summutab madalad sagedused.
- Kasutus: Kasutatakse rakendustes, kus on vaja edastada kõrgsageduslikke signaale ja blokeerida madalsageduslikud komponendid, näiteks helisüsteemides või raadiosageduslikes vastuvõtjates.
- Ehitus: Tavaliselt koosneb kondensaatorist ja induktiivpoolist, kus kondensaator on signaaliteel ja induktiivpool ühendatud maaga, mis summutab madalsagedusi.
- Tüüpiline rakendus: Kõrgsageduslike signaalide filtreerimine antennides, raadiosagedusfiltrid, helisüsteemides kõrgete sageduste edastamine.
- Ribapääsfilter (Band-pass filter):
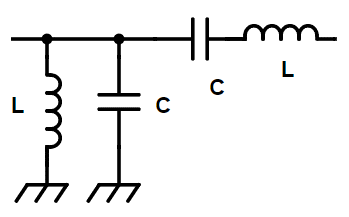
- Funktsioon: Laseb läbi ainult kindla sagedusriba ning summutab sagedused, mis jäävad sellest ribast kõrgemale või madalamale.
- Kasutus: Kasutatakse raadiosageduslikes rakendustes, kus soovitakse edastada ainult teatud sagedusala, näiteks raadiovastuvõtjates või traadita side süsteemides.
- Ehitus: Koosneb kahest LC komponendist (induktiivpool ja kondensaator), kus ühe kombinatsioon määrab filtri alumise piirsageduse ja teine kombinatsioon määrab ülemise piirsageduse.
- Tüüpiline rakendus: Raadio ja telekommunikatsiooniseadmed, sagedusmodulaatorid, võimendid.
- Ribakõrvalefilter (Band-stop filter):

- Funktsioon: Blokeerib kindla sagedusriba ja laseb läbi signaalid, mis on sellest ribast kas kõrgemal või madalamal.
- Kasutus: Kasutatakse süsteemides, kus on vaja summutada kindlaid sagedusi, näiteks häirivate sageduste või resonantsi eemaldamiseks.
- Ehitus: Tavaliselt sisaldab LC komponente nii, et nende kombinatsioon määrab kindla sagedusala, mis suletakse.
- Tüüpiline rakendus: Müra või ebasoovitavate sageduste eemaldamine raadio- ja sidevahendites, elektromagnetiliste häirete vähendamine.
LC-FILTRITE KASUTUSALAD:
- Toiteallikad:
- Madalsagedusfiltrid kasutatakse alalisvoolu toiteallikates, et eemaldada vahelduvvoolu komponendid ja stabiliseerida alalisvoolu väljund.
- Raadiosageduslikud (RF) ahelad:
- Kõrgsagedusfiltrid ja ribapääsfiltrid leiavad kasutust raadiosageduslikes ahelates, näiteks raadiovastuvõtjates ja antennides, kus need aitavad kindla sagedusriba signaale edastada ja müra blokeerida.
- Helisüsteemid:
- Madalsagedusfiltrid ja kõrgsagedusfiltrid kasutatakse helisüsteemides, et filtreerida teatud sagedusvahemikud ja edastada ainult soovitud helikomponendid. Näiteks madalpääsfiltrid suunavad madalaid helisagedusi bassikõlaritesse ja kõrgpääsfiltrid suunavad kõrgsageduslikke helisid tweeter’itesse.
- Elektromagnetilise ühilduvuse (EMC) tagamine:
- Ribakõrvalefiltrid on olulised elektromagnetiliste häirete (EMI) eemaldamiseks, et vältida häireid teistest seadmetest või süsteemi enda sisemisi häireid.
LC-filtrid on väga olulised elektroonikas, kuna need võimaldavad soovitud signaalide edastamist ja soovimatute sageduste summutamist, mis tagab parema signaali kvaliteedi ja seadmete töökindluse.
Kokkuvõttes on filtreerimine ja silumine väga oluline funktsioon elektroonikaseadmetes, et hoida signaalid ja pinge võimalikult stabiilsena, eemaldades soovimatud sagedused ja vähendades müra.
3. SIGNAALIDE EDASTAMINE JA VASTUVÕTT
Raadiovastuvõtjates ja saatjates kasutatakse mähiseid sageduse selekteerimiseks ja võimendamiseks. Mähised aitavad luua resonantssagedusi, mis on vajalikud täpsete raadiosignaalide eristamiseks ja võimendamiseks.
Raadiovastuvõtjates ja saatjates mängivad mähised olulist rolli signaalide selekteerimisel ja võimendamisel. Need komponendid on vajalikud raadiosageduslike signaalide töötlemiseks ja täpsete sageduste eraldamiseks paljude teiste sageduste seast. Mähised töötavad tavaliselt koos kondensaatoritega, moodustades LC-ahelaid, mis võimaldavad resonantsi, et häälestuda soovitud sagedustele. Selgitame allpool põhjalikumalt, kuidas mähised töötavad ja milleks neid raadiovastuvõtjates ja saatjates kasutatakse.
SAGEDUSE SELEKTEERIMINE LC-RESONANTSAHELA ABIL
Raadiovastuvõtjates ja -saatjates on vaja valida täpne sagedus, et eraldada soovitud raadiosignaal paljude teiste signaalide ja mürade seast, mis levivad samaaegselt õhus. Selleks kasutatakse mähiseid koos kondensaatoritega LC-resonantsahelates.
RESONANTSAHEL:
- LC-ahel koosneb mähisest (L) ja kondensaatorist (C), mis töötavad koos resonantsi loomiseks. Resonants tekib siis, kui induktiivpooli ja kondensaatori reaktiivtakistused tasakaalustavad teineteist, tekitades süsteemi jaoks spetsiifilise resonantssageduse ((f_r)).
Resonantssageduse valem on järgmine:
- L – mähise induktiivsus (henrites, H)
- C – kondensaatori mahtuvus (faradites, F)
- (f_r) – resonantssagedus (hertsides, Hz)
Selle valemi abil saab LC-ahel häälestuda kindlale sagedusele, kus mähise ja kondensaatori reaktiivtakistused üksteist tühistavad, võimaldades ainult selle sageduse läbimist. See tähendab, et ainult resonantssagedusega signaal pääseb edasi, samal ajal kui teised sagedused summutatakse. Sageduse selekteerimine on vajalik, et raadiovastuvõtja saaks tuvastada ja töödelda just seda konkreetset signaali, millele see on häälestatud (nt raadiojaam).
NÄIDE:
Kui soovid kuulata 98 MHz raadiojaama, peab raadiovastuvõtja LC-ahel olema häälestatud resonantssagedusele 98 MHz. Ahel blokeerib kõik teised sagedused peale 98 MHz, võimaldades edastada vaid soovitud raadiosignaali.
SIGNAALI VÕIMENDAMINE
Pärast sageduse selekteerimist vajavad vastuvõetud signaalid sageli täiendavat võimendamist, kuna raadiosignaalid võivad olla väga nõrgad. Mähised aitavad võimendamise protsessis mitmel viisil.
A. VÕIMENDUSTRAFOD:
- Raadiovastuvõtjates ja saatjates kasutatakse mähiseid tihti trafodena, et võimendada või muuta signaali pinge taset. Trafosid kasutatakse signaalide pinge tõstmiseks või langetamiseks sõltuvalt süsteemi vajadustest.
- Kui signaal on väga nõrk, võib primaarmähise magnetväli indutseerida tugevama voolu sekundaarmähises, tõstes seeläbi signaali pinge taset. See on oluline eriti AM- ja FM-raadiovastuvõtjates, kus signaale tuleb tugevdada enne nende töötlemist ja muutmist kuuldavaks heliks.
B. SUURENENUD SIGNAALIKVALITEET:
- Mähised aitavad ka signaale stabiliseerida ja võimendada, vähendades müra ja häireid. See võimaldab vastuvõetaval signaalil olla puhtam ja täpsem, mis parandab vastuvõtja üldist jõudlust ja tagab parema kuulamiskogemuse.
RESONANTSI LOOMINE RAADIOSAGEDUSTE JAOKS
Resonants on raadiosüsteemide jaoks äärmiselt oluline. Mähised aitavad luua resonantssagedusi, mis on vajalikud teatud raadiosageduslike signaalide täpseks eraldamiseks ja võimendamiseks. Resonants võimaldab vastuvõtjal töötada täpselt selle sagedusega, mida soovitakse kuulata või saata, samal ajal kui kõik teised sagedused blokeeritakse või ignoreeritakse.
A. VASTUVÕTJATES:
- Vastuvõtjad kasutavad resonantsahelaid, et häälestuda kindlale sagedusele, näiteks konkreetsele raadiojaamale või saatjale. Mähis LC-ahelas aitab täpselt valida selle sageduse, kus signaal on kõige tugevam ja puhtam. Kuna raadiovastuvõtjate antennid püüavad kinni palju erinevaid sagedusi, aitab resonants neilt soovitud sagedust eristada.
B. SAATJATES:
- Raadiosaatjad kasutavad resonantsi, et edastada signaale kindlal sagedusel. See tagab, et signaalid edastatakse täpselt määratud sagedusel, vältides segadust teiste sagedustega ja võimaldades saatjal edastada täpse signaali valitud vahemikus.
KASUTAMINE RAADIO JA RAADIOSAGEDUSLIKES RAKENDUSTES
Mähised on olulised mitte ainult traditsioonilistes AM- ja FM-raadiotes, vaid ka paljudes muudes raadiosageduslikes rakendustes, nagu:
- Mobiilsides: Mähised aitavad mobiilsidesüsteemides selekteerida ja võimendada erinevaid sagedusi, mida kasutatakse andmeside edastamiseks.
- Wi-Fi ja Bluetooth-seadmetes: Need seadmed kasutavad sarnaseid sageduse selekteerimise ja võimendamise tehnikaid mähiste ja kondensaatorite abil.
- Saatjate ja vastuvõtjate antennides: Antennides, mis edastavad ja vastuvõtavad signaale, kasutatakse mähiseid signaali kvaliteedi ja tugevuse parandamiseks.
KOKKUVÕTE
Mähised on raadiovastuvõtjates ja -saatjates hädavajalikud komponendid, mis aitavad valida ja võimendada signaale. Mähised moodustavad koos kondensaatoritega LC-resonantsahelaid, mis võimaldavad süsteemil häälestuda kindlatele sagedustele, jättes kõrvale kõik teised sagedused. Pärast soovitud sageduse valimist aitavad mähised ka signaali võimendada, et seda oleks lihtsam töödelda ja edastada. Tänu nendele omadustele on mähised kriitilise tähtsusega raadiosageduskommunikatsioonis ja paljudes muudes elektroonikaseadmetes.
4. TRAFO PÕHIMÕTE JA MUTUAALNE INDUKTSIOON
Kahe või enama mähise vahel võib tekkida mutuaalne induktsioon, kus ühe mähise magnetväli indutseerib teises mähises voolu. Seda põhimõtet kasutatakse trafodes, mis võimaldavad pinget tõsta või langetada, samuti energia ülekandmiseks ühest ahelast teise ilma füüsilise ühenduseta.
5. ELEKTROMAGNETID (SOLENOIDID)
Mähised võivad luua tugeva magnetvälja, kui vool läbib neid, ning neid kasutatakse elektromagnetides, näiteks releedes, elektrimootorites ja generaatorites.
LINEAARLIIKUMISEGA SOLENOID
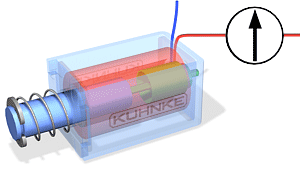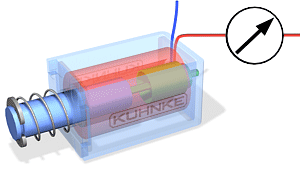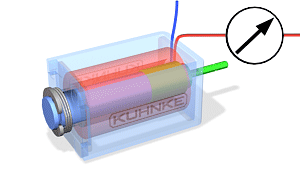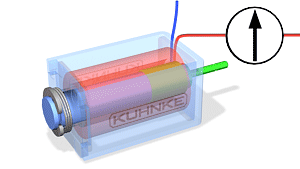
Lineaarliikumisega solenoidil (Joonis) on kolm tähtsat tunnust: käigupikkus, jõud ja töötsükkel.
Käigupikkus on kaugus kuhu solenoidi südamik liigub.
Jõudu võib defineerida liikumise alguses liikumises, lõppedes või kogu liikumise jooksul. Jõud on alguses väiksem kui liikumise lõpus.
Töötsükkel on väljendatud protsendina (Näitab kui suure osa moodustab sisselülitamisaeg kogu tsükli ajast.)
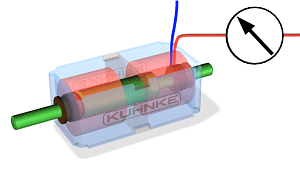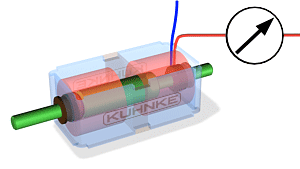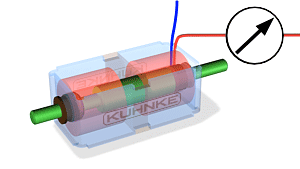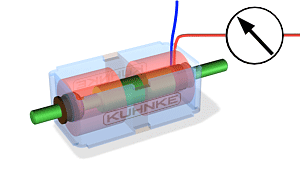
KAHE SUUNALISED LINEAARLIIKUMISEGA SOLENOIDID
Kahe suunalised lineaarliikumisega solenoidid.
Kahesuunalised lineaarliikumisega solenoidid puhul kasutatakse tavaliselt kahte erineva polaarsusega mähist.
BISTABIILSED SOLENOID
Bistabiilsel solenoidil on kaks stabiilset positsiooni, solenoidmähise konstruktsioonis on püsimagnetid, mis võimaldavad südamikul kindla positsiooni säilitada ka pärast elektriimpulssi. Perspektiivis on bistabiilsel solenoidil kaks stabiilset seisundit. Esiteks- kui solenoidile on elektriliselt rakendatud ja südamik on täielikult väljas ja teiseks – kui solenoid on ilma vooluta ning südamik fikseeritakse püsimagnetitega (Joonis 3.4)
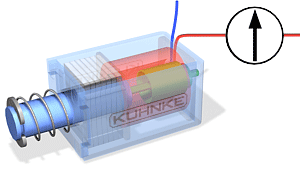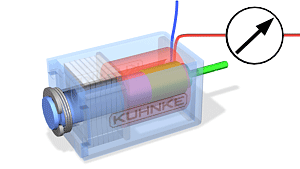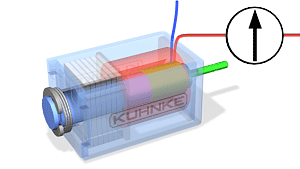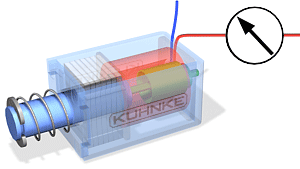
PÖÖRDLIIKUMISEGA SOLENOIDID
Põhiliselt kasutatakse kahte tüüpi pöördliikumisega solenoide:
Ühesuunalise pöördliikumisega solenoidid (solenoidmähisest arendatav jõud on ühesuunaline ja tagastust toimub mehaaniliselt, kõige sagedamini vedruga).
Kahesuunalise pöördliikumisega solenoidid (kasutatakse kahte pooli, – kiirendust muudetakse keerdude arvuga)


Ühesuunalise pöördsolenoide maksimaalne pöördenurk on reeglina 95 ° ja kahesuunalise pöördsolenoidi pöördenurgad ei ületa 45 °. Automaatikas kasutatakse suhteliselt arva ka suurema pöördenurgaga pöördsolenoide.
HOIDESOLENOIDID EHK HOIDEMAGNETID
Hoidesolenoidid ehk hoidemagnetid on ilma liikuva südamikuta elektromagnetid, mis omavad suurt hoidejõudu (alates 250 kg hoidejõuga magneteid kasutatakse uste sulgemiseks … üle 700 kg hoidejõuga magneteid kasutatakse turvalukkudes)

OLULISED PARAMEETRID
Mähise toimivust ja omadusi mõjutavad mitmed parameetrid:
- Induktiivsus (L) – mõõdetakse henrites (H). Suur induktiivsus tähendab, et mähis suudab rohkem energiat magnetvälja kujul salvestada.
- Maksimaalne voolutugevus – määrab, kui palju voolu mähis suudab taluda ilma ülekuumenemiseta või füüsilise kahjustuseta.
- Tööpiirkond (sagedusvahemik) – sõltuvalt südamiku materjalist ja konstruktsioonist võib mähis olla sobilik kas madala või kõrge sagedusega signaalide jaoks.
- Mähise takistus – mähise traadil on ka teatav elektriline takistus, mis võib põhjustada soojuskaod.
KOKKUVÕTE
Induktiivpool ehk mähis on elektroonikas ja elektrotehnikas oluline komponent, mille põhifunktsiooniks on energia salvestamine magnetvälja kujul ning voolu muutuste takistamine. Mähised on hädavajalikud nii energiat salvestavates vooluahelates, signaalide töötlemises kui ka pinge ülekandmises trafo kaudu. Erinevad mähise tüübid on kohandatud eri rakenduste jaoks, pakkudes optimaalset lahendust vastavalt kasutusvaldkonnale ja nõuetele.
Induktiivpool
Induktiivpool (lühidalt: pool) on elektroonikakomponent, mida kasutatakse elektriahelates võnkeringide ja filtrite induktiivelemendina. Pooli põhiline tunnussuurus on elektriline induktiivsus.
Induktiivpooli, millega vähendatakse koormusahelas voolu vahelduvkomponenti või tõkestatakse teatud sagedusest kõrgemate sageduskomponentide edasipääsu, nimetatakse paispooliks ehk drosseliks.

EHITUS



Pool koosneb alusest ja sellele mähitud mähisest. Alusele mähitud poolidel võib olla üks või mitu mähist. Samuti võivad ühe mähise osad olla alusele mähitud sektsioneeritult, ühekihilised mähised kindla keerusammuga.
Väikese induktiivsusega poolide puhul võib poolialus ka puududa. Kõrgsageduspoolid, mis on mähitud jämedast vask- või hõbetatud traadist, võivad olla ka ilma aluseta (mähitud vastava jämedusega alusele ja seejärel alus eemaldatud).
Selleks et vähendada pooli mõõtmeid ja võimaldada induktiivsust teatud piirides sujuvalt reguleerida, kasutatakse suurt magnetilist läbitavust omavat ferriitsüdamikku. Ülikõrgsageduspoolides kasutatakse diamagnetilisest metallist (nt vasest) südamikke; need mõjuvad induktiivsust vähendavalt.
Parasiitsidestuste tekkimise vältimiseks varjestatakse induktiivpoolid vask- või alumiiniumplekist varjega.
- Mitmesuguseid induktiivpoole
- Raadiosageduspoole
(all: ferriitantenn kesk- ja pikklainele) - Lameda ferriitsüdamikuga pool trükilülitusele
- Induktiivkomponendid (värvimarkeeringuga)
MÄHISTE LIIGID
Pooli mähise kuju ja mähkimisviisi alusel eristatakse järgmisi mähiseid:
- ühe- ja mitmekihiline tihemähis – mähitakse keerd keeru kõrvale ja vajadusel mähisekihid üksteise peale;
- samm-mähis – mähitakse traadi läbimõõdust suurema keerusammuga;
- sektsioonmähis – koosneb ühisele pikiteljele või alusele mitmest jadamisi mähitud ja omavahel ühendatud mähiseosast;
- ristmähis – mähise naaberkihtides olevad mähisekeerud on omavahel mähitud mingi nurga all;
- vabamähis – mähitakse vabalt (korrapäratult) aluse otsketaste ehk põskede vahele;
- sümmeetriline mähis – saadakse kahe juhtmega korraga mähkimisel, kui ühe juhtme lõpp ühendada teise juhtme algusega, ühendamiskoht on mähise keskharund ehk keskväljaviik.

INDUKTIIVPOOLI TUNNUSSUURUSED JA ASESKEEM
- Induktiivsus
on võrdeline mähise keerdude arvu ruuduga ning sõltub ka mähise kujust ning südamiku materjalist;
- Hüvetegur
on pooli induktiivtakistuse
ja poolis tekkiva kõrgsagedustakistuse
suhe:
;
- Omamahtuvus
sõltub mähise keerdudevahelisest hajumahtuvusest
;
- Induktiivsuse temperatuuritegur
näitab induktiivsuse suhtelist muutumist temperatuurimuutumisel 1 K võrra.
Kaotakistuste ja omamahtuvuse tõttu kujuneb Induktiivpooli või drosseli aseskeemmitmekomponendiliseks.
SÜDAMIKUTA INDUKTIIVPOOLID
Järgmiste valemite abil saab võrdlemisi täpselt arvutada südamikuta pooli induktiivsust ja keerdude arvu. Kõigis valemites on induktiivsus mikrohenrides (μH) ja poolide mõõtmed millimeetrites.
ÜHEKIHILINE TIHEMÄHISEGA INDUKTIIVPOOL
Ühekihilise tihemähisega induktiivpoole kasutatakse enamasti sagedusel üle 500 kHz. Mähis võib olla mähitud poolialusele tihedalt keerd keeru kõrvale või suurendatud sammuga, s.t mähis mähitakse traadi diameetrist suurema sammuga; mähise keerdude vahele jäävad siis vahed. Suurendatud sammuga poolid on väikese omamahtuvuse ja suure hüveteguriga (

Ühekihilise pooli induktiivsus
kus
‒ pooli keerdude arv;
‒ keeru läbimõõt, s.o poolialuse läbimõõdu
ja traadi läbimõõdu
summa;
‒ mähise pikkus.
Sellesama valemiga saab arvutada ka samm-mähisega ühekihilise pooli (solenoidi) induktiivsuse. Mähise samm
Kui on tarvis leida nõutava induktiivsuse 



MITMEKIHILINE INDUKTIIVPOOL
Mitmekihilise pooli induktiivsus
kus
‒ mähise keerdude arv;
‒ mähise keskmine läbimõõt;
‒ mähise pikkus;
‒ mähise kõrgus.
Traadi kindla pikkuse korral saadakse suurima induktiivsusega pool sel juhul, kui 

Et mähise mõõtmed olenevad keerdude arvust, ei saa neid mõõtmeid täpselt ette anda. Seepärast tuleb keerdude arv leida järkjärgulise lähendamise teel: arvutada orienteeriv keerdude arv mähise eeldatavate mõõtmete alusel, siis täpsustada mõõtmeid 

LAMEMÄHISEGA INDUKTIIVPOOLID
Lamemähisega induktiivpoolid on omadustelt võrreldavad ühekihiliste samm-mähisega poolidega. Neil trükimenetlusel valmistatavatel poolidel on väike omamahtuvus, suur hüvetegur ja stabiilsed parameetrid. Lamemähisega poolid on harilikult ring- või ruutspiraalse kujuga. Järgmistes arvutusvalemites on induktiivsus mikrohenrides ja mõõtmed millimeetrites.
Ringspiraalse lamepooli induktiivsus

Nõutava induktiivsuse saamiseks vajalik ringspiraalse pooli keerdude arv
Nendes valemites
– kujutegur, mis saadakse suhte
alusel diagrammilt;
– pooli suurim välisläbimõõt (mm);
– pooli väikseim siseläbimõõt (mm).
Spiraali moodustavate poolringide tsentrite vahe 


Ruutspiraalse lamepooli induktiivsus
Nõutava induktiivsuse saamiseks vajalik ruutspiraalse pooli keerdude arv
Nendes valemites
– kujutegur, mis saadakse suhte
alusel diagrammilt;
– pooli suurim küljepikkus väljast (mm);
– pooli väikseim küljepikus seest (mm).
SÜDAMIKUGA INDUKTIIVPOOLID
MAGNETSÜDAMIKUD
Kõrgsageduspoolide ja –drosselite valmistamisel kasutatakse pehmemagnetferriiti, varem ka magnetodielektrikuid, näiteks karbonüülrauda. Pehmemagnetferriidid, välja arvatud mangaantsinkferriit, on kasutatavad üldiselt nõrgas magnetväljas.
Ferromagnetilisi südamikke iseloomustab
- efektiivne magnetiline läbitavus
‒ südamikuta pooli induktiivsuse ja samasuguse südamikuga pooli induktiivsuse suhe;
- südamiku hüvetegur – kaonurga tangensi
pöördväärtus; mida suurem on südamiku kaoenergia, seda väiksem on selle hüvetegur;
- südamiku parameetrite stabiilsus – seda väljendab magnetilise läbitavuse temperatuuritegur, mis võrdub südamiku efektiivse magnetilise läbitavuse suhtelise muutusega temperatuuri muutumisel ühe Kelvini kraadi võrra.
Induktiivpoolidele valmistatakse ferriidist varrassüdamikke, plaatsüdamikke, keermestatud häälestussüdamikke, keermestatud plastpeaga häälestussüdamikke, ferriidist rõngas- ehk toroidsüdamikke, karbonüülrauast ja ferriidist ummis- ehk mantelsüdamikke.
FERRIITSÜDAMIKUGA POOLID
Silindrilise ferriitsüdamikuga poolidel on suur hüvetegur ja väiksemad mõõtmed kui südamikuta poolidel. Südamiku kasutamisel poolis nõrgeneb pooli puisteväli, samuti lihtsustub pooli häälestamine.
Südamikuga pooli induktiivsus
FERRIIDIST RÕNGASSÜDAMIKUGA INDUKTIIVPOOLID
Ferriidist rõngassüdamikku kasutatakse, kui on vaja minimaalsete mõõtmete juures maksimaalset induktiivsust. Rõngassüdamikuga poolide eeliseks on väike magnetvoo hajumine, puuduseks suhteliselt keeruline mähkimine ja induktiivsuse sujuva reguleerimise võimaluse puudumine.
Rõngassüdamikuga pooli induktiivsus (mikrohenrides):
kus
– südamiku materjali dünaamiline magnetiline läbitavus,
– südamiku ristlõike pindala (ruutsentimeetrites),
– magnetjõujoonte keskmine pikkus (sentimeetrites),
Pooli keerdude arv
kus
– pooli vajalik induktiivsus (µH),
– rõnga välisläbimõõt (mm),
– rõnga siseläbimõõt (mm),
– südamiku materjali suhteline magnetiline läbitavus,
– südamiku kõrgus (mm).
MANTELSÜDAMIKUGA INDUKTIIVPOOLID
Mantelsüdamikuga poolidele on omane suur hüvetegur ja varjestusaste ning väike omamahtuvus. Südamiku konstruktsioonist tulenev magnetvarjestustoime ei välista vajadusel elektrostaatilist varjestamist.
Mantelsüdamikuga poolide induktiivsus arvutatakse samamoodi nagu silindrilise südamikuga pooli korral.
DIAMAGNETSÜDAMIKUGA INDUKTIIVPOOLID
Diamagnetsüdamikuga induktiivpoolidel on induktiivsuse vähendamiseks mittemagnetilisest metallist (vask, alumiinium, valgevask) südamik. Diamagnetsüdamikuga on võimalik induktiivsust vähendada 10…15%. Mittemagnetiline südamik vähendab oluliselt pooli hüvetegurit. Kõige väiksemad kaod on puhtast vasest südamiku korral. Teistest metallidest südamike kasutamisel suureneb kadu võrdeliselt vase elektritakistuse ja kasutatava metalli elektritakistuse suhtega.
INDUKTIIVPOOLIDE VARJESTUS
Poolide varjestamist kasutatakse neil juhtudel, kui on vaja ära hoida poolidevahelist parasiitsidestust. Parasiitsidestust tekitab poolide ümber olev magnetväli.
Varje mõjul väheneb pooli induktiivsus ja hüvetegur ning suureneb omamahtuvus. Pooli andmete muutumine on seda suurem, mida lähemal on varje pooli mähise keerdudele.
Poolide varjestamiseks kasutatakse alumiinium-, vask- või valgevaskplekist silindrilisi või ristkülikukujulisi topsikuid. Sageli tehakse kõrgsageduspoolide varjetesse avad, et oleks võimalik keerata häälestamiseks poolisüdamikke.














