Elektrotehnika ja elektroonika alused
Peatükk 1: Põhimõisted
1. Sissejuhatus
1.1 Mõisted ja põhialused
Elektrotehnika ja elektroonika ajalugu
Elektrotehnika ja elektroonika arengulugu on tihedalt seotud inimkonna tehnoloogilise edenemisega. Esimesed sammud tehti antiikajal, kui avastati staatiline elekter, kuid tõeline läbimurre toimus alles 18. ja 19. sajandil. Selle perioodi teadlased, nagu Michael Faraday ja André-Marie Ampère, panid aluse elektromagnetismile, mis on elektrotehnika ja elektroonika aluseks. Faraday avastas elektromagnetilise induktsiooni, mis võimaldas arendada elektrigeneraatoreid ja mootoreid, samas kui Ampère kirjeldas elektrivoolude magnetilist mõju, aidates seeläbi mõista elektri ja magnetismi vahelist seost.

Michael Faraday katsetamas elektromagnetilise induktsiooni nähtust
Pildil on kujutatud Faraday kuulsat eksperimenti, kus ta avastas, et muutuv magnetväli võib tekitada elektrivoolu.
James Clerk Maxwelli töö 19. sajandi keskel sidus need avastused ühtseks teoreetiliseks raamistikuks, tuues välja neli põhivõrrandit, mis kirjeldavad elektri ja magnetismi põhilisi seaduspärasusi. Need võrrandid on tänapäevase elektromagnetismi aluseks.

Maxwelli maailm
Maxwelli nelja põhivõrrandid, mis kirjeldavad elektri- ja magnetväljade vahelist suhet.
19. sajandi lõpp tõi kaasa elektrienergia tootmise ja jaotamise tehnoloogiate arengu. Thomas Edison ja Nikola Tesla olid selle perioodi juhtivad figuurid. Edison pooldas alalisvoolu (DC) süsteemi, mis oli sobiv lühikeste vahemaade jaoks, samas kui Tesla tutvustas vahelduvvoolu (AC) süsteemi, mis osutus tõhusamaks elektri edastamisel pikkade vahemaade taha. AC-süsteem on siiani kasutusel kogu maailmas.
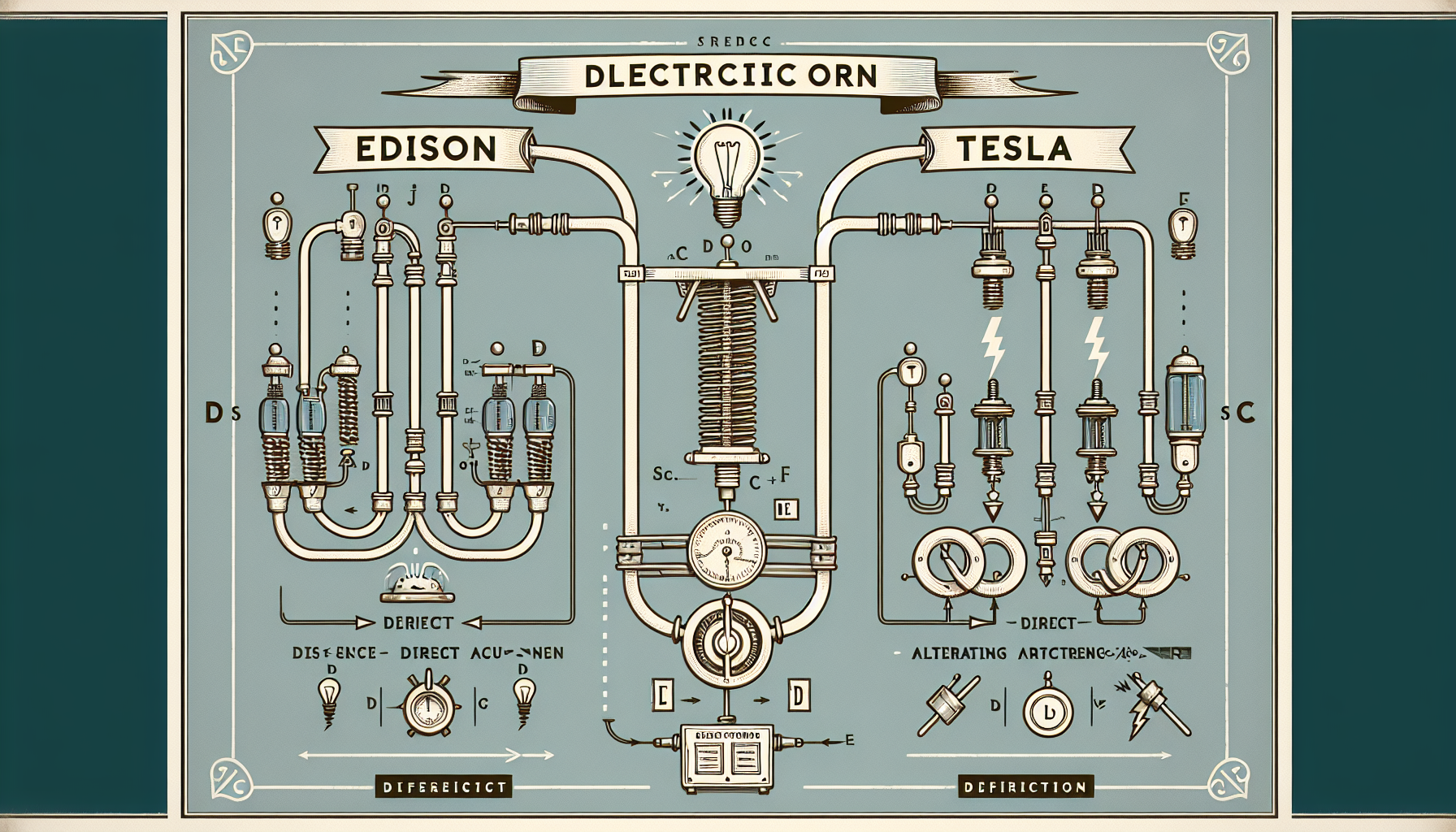
Edisoni ja Tesla elektrisüsteemide võrdlus
Skeem näitab alalisvoolu ja vahelduvvoolu süsteemide erinevusi ja kasutusviise.
20. sajandil toimus järgmine suur areng, kui alustati pooljuhttehnoloogiate kasutuselevõttu. Pooljuhtide avastamine ja nende kasutamine transistoride ja integreeritud vooluringide (IC) tootmises viis elektroonika revolutsioonini. See võimaldas arendada kaasaegset arvutustehnikat, telekommunikatsiooni ja palju teisi valdkondi, mis on tänapäeval igapäevaelu lahutamatud osad.

Esimene transistori 23. detsember 1947
Esimene transistor loodi 1947. aastal Bell Laboratoriesis Ameerika Ühendriikides. Selle leiutasid kolm teadlast: John Bardeen, Walter Brattain ja William Shockley. See esimene transistor oli tuntud kui punktkontakttransistor ja see koosnes kahest kullast kontaktist, mis puudutasid kergelt germaaniumist pooljuhti. See seade võimaldas võimendada elektrisignaale, olles esimene samm tänapäeva elektroonika arengus.

Transistori leiutamine tähistas elektroonikatööstuse revolutsiooni, kuna see asendas suured ja ebaefektiivsed vaakumtorud, mida varem kasutati. Transistoride väiksus, töökindlus ja madal energiatarve sillutasid teed kaasaegsetele arvutitele, telekommunikatsiooniseadmetele ja paljudele muudele tehnoloogiatele, mida me täna kasutame.
Valdkonna tähtsus
Elektrotehnika ja elektroonika on tänapäeval ühed kõige olulisemad ja laiemalt levinud inseneriteaduse valdkonnad. Need valdkonnad mõjutavad igapäevaelu laialdaselt – alates elektrivõrkudest, mis toidavad meie kodusid ja tööstust, kuni nutiseadmeteni, mis hoiavad meid ühenduses ja võimaldavad juurdepääsu informatsioonile.
- Elektrotehnika hõlmab elektrienergia tootmist, edastamist ja jaotamist. See võimaldab meil kasutada elektrienergiat valgustuseks, kütmiseks ja tööstusprotsesside jaoks.
- Elektroonika keskendub elektrisignaalide töötlemisele ja kontrollimisele, olles aluseks kõigile digitaalsetele seadmetele, alates koduelektroonikast ja arvutitest kuni keeruliste juhtimissüsteemideni tööstuses.
Energia tootmine
Energia tootmine ja ülekanne moodustavad aluse kaasaegsele tsivilisatsioonile, võimaldades elektrienergiat jõuda kõikjale, kus seda vajatakse – alates kodudest ja kontoritest kuni suurte tööstuskompleksideni.

Soojus elektrijaam SEJ on elektrijaam, mis kasutab soojusenergiat elektrienergia tootmiseks. Need jaamad põhinevad põhimõttel, et kütuse (nagu kivisüsi, maagaas, nafta või biomass) põletamisel vabanev soojusenergia muundatakse mehaaniliseks energiaks, mida kasutatakse elektrigeneraatori käivitamiseks.
Kuidas soojus elektrijaam töötab?
- Kütuse põletamine: Elektrijaama süda on katel, kus kütust põletatakse, et toota kõrgetemperatuurilist kuuma auru. Traditsiooniliselt kasutatakse kütustena kivisütt, maagaasi või naftat, kuid üha rohkem kasutatakse ka taastuvallikaid nagu biomass.
- Auru tootmine: Kütuse põletamisel vabanev soojusenergia kasutatakse vee aurustamiseks. Suurtes kateldes kuumutatakse vesi kõrgtemperatuuriliseks auruks, mille rõhk on väga suur.
- Auruturbiin: Kuum aur suunatakse auruturbiini, kus see laieneb ja annab oma energia turbiini labadele, pannes turbiini pöörlema. Turbiini pöörlev liikumine muudetakse mehaaniliseks energiaks.
- Elektrigeneraator: Turbiini pöörlemine käitab generaatorit, mis muundab mehaanilise energia elektrienergiaks elektromagnetilise induktsiooni abil. Tekkinud elektrienergia suunatakse jaotussüsteemi kaudu tarbijateni.
- Aurukondensatsioon ja ringlus: Pärast auruturbiinis kasutamist juhitakse aur läbi kondensaatori, kus see jahutatakse ja muudetakse tagasi veeks. Seejärel suunatakse vesi tagasi katlasse, et alustada uut tsüklit.
Tõhusus ja keskkonnamõju
Soojus elektrijaamade tõhusus on piiratud, kuna osa soojusest kaotatakse süsteemis ja see ei muundu elektrienergiaks. Keskmine soojus elektrijaama tõhusus on umbes 33–40%, kuid see võib olla suurem kombineeritud soojuse ja elektri tootmise süsteemides.
Soojus elektrijaamad on sageli seotud oluliste keskkonnamõjudega. Kütuste põletamisel tekib suur hulk süsinikdioksiidi (CO2) ja muid kasvuhoonegaase, mis aitavad kaasa kliimamuutusele. Samuti võivad tekkida muud saasteained, nagu vääveldioksiid (SO2) ja lämmastikoksiidid (NOx), mis põhjustavad õhusaastet ja happevihmasid.
Tulevikusuunad
Tänu kasvavale keskkonnateadlikkusele ja rahvusvahelistele kliimakokkulepetele otsitakse pidevalt viise, kuidas vähendada soojus elektrijaamade mõju keskkonnale. Selleks kasutatakse:
- Tõhusamaid tehnoloogiaid: Arendatakse kõrgemat temperatuuri taluvaid materjale ja uusi protsesse, mis võimaldavad soojus elektrijaamadel töötada kõrgema tõhususega.
- CO2 sidumine ja säilitamine (CCS): Tehnoloogiad, mis püüavad kinni ja ladustavad süsinikdioksiidi, et vähendada kasvuhoonegaaside heitmeid.
- Üleminek taastuvenergiale: Paljud riigid on hakanud vähendama sõltuvust fossiilkütustel põhinevatest soojus elektrijaamadest ja suurendavad investeeringuid taastuvenergia lahendustesse, nagu tuule- ja päikeseenergia.
Kokkuvõttes mängivad soojus elektrijaamad olulist rolli ülemaailmses elektrienergia tootmises, kuid samas esitatakse neile tõsiseid väljakutseid, mis on seotud nende keskkonnamõjudega ja vajadusega leida kestlikumaid lahendusi.

Olkiluoto tuumaelektrijaam on tuumaelektrijaam, mis asub Soomes Rauma lähedal Olkiluoto saarel. 1979. aastal käiku antud jaamas on kolm tuumareaktorit.Pärast kolmanda rektori täisvõimsuse saavutamist 2022. aastal on jaama koguvõimsus 3380 MW. Kolmanda reaktori ehitamine venis 12 ja pool aastat üle kavandatudaja.
Tuumajaam on elektrijaam, mis kasutab tuumaenergia vabastamiseks tuumareaktsioone, tavaliselt tuuma lõhustumist, et toota elektrienergiat. Tuumaenergia on väga võimas energiallikas, mis võimaldab väikese kütusekoguse abil toota suures koguses elektrit.
Tuumajaama tööpõhimõte
- Tuumakütus ja tuumareaktsioon:
- Tuumajaamas kasutatakse tavaliselt uraani või plutooniumi isotoope tuumakütusena. Kõige sagedamini kasutatakse uraani-235 isotoopi.
- Tuumareaktsioon algab, kui neutron tabab uraani või plutooniumi aatomituuma, põhjustades selle lõhustumist. Lõhustumisel eraldub suur hulk energiat soojusena ning vabaneb rohkem neutroneid, mis võivad omakorda tabada teisi tuumi, käivitades ahelreaktsiooni.
- Soojusenergia tootmine:
- Lõhustumise käigus vabanenud soojusenergia kantakse üle reaktori jahutusvedelikule, mis on tavaliselt vesi. Vesi imab soojuse ja muutub kõrgtemperatuuriliseks auruks.
- Reaktori südamiku ümber olev jahutusvedelik tsirkuleerib pidevalt, hoides reaktori temperatuuri kontrolli all ja kandes soojuse edasi järgmisse etappi.
- Auruturbiin:
- Kuum aur, mis on toodetud reaktorist eraldunud soojusega, juhitakse suure surve all auruturbiini.
- Auruturbiin, mis on ühendatud elektrigeneraatoriga, hakkab aururõhu tõttu pöörlema. See pöörlev liikumine muundatakse elektrienergiaks generaatori abil, kasutades elektromagnetilist induktsiooni.
- Aurukondensatsioon ja jahutus:
- Pärast turbiinist väljumist suunatakse aur läbi kondensaatori, kus see jahutatakse ja muudetakse tagasi veeks. Kondensaatoris kasutatakse sageli väljastpoolt tulevat jahedat vett, näiteks jõest või jahutustornidest pärit vett.
- Vesi, mis on muudetud tagasi vedelasse olekusse, pumbatakse tagasi reaktorisse, kus tsükkel algab uuesti.
- Elektrienergia jaotamine:
- Generaatoris toodetud elektrienergia suunatakse elektrivõrku, kust see jaotatakse tarbijateni – kodudesse, ettevõtetesse ja tööstustesse.
Ohutus ja kontrollsüsteemid
Tuumajaamades on olemas mitmeid ohutussüsteeme, et hoida tuumareaktsioon kontrolli all ja vältida õnnetusi:
- Kontrollvardad: Kontrollvardad, mis on valmistatud materjalidest, mis neelavad neutroneid (nt boor või kadmium), kasutatakse tuumareaktsiooni reguleerimiseks. Vajaduse korral saab neid vardaid reaktorisse sisestada, et aeglustada või peatada ahelreaktsioon.
- Hädaolukorra jahutussüsteemid: Need süsteemid on loodud tagama reaktori jahutuse ka avariiolukordades, vältides kütuseelementide ülekuumenemist ja võimalikke tuumakatastroofe.
- Jahutustornid: Suuremad tuumajaamad kasutavad jahutustorne, et hajutada liigset soojust atmosfääri, vähendades jaama keskkonnamõjusid.
Tuumaenergia eelised ja väljakutsed
Eelised:
- Väike kütusekulu: Väikese koguse tuumkütusega saab toota suures koguses energiat.
- Väiksemad CO2 heitmed: Tuumaelektrijaamad ei tekita kasvuhoonegaase, mis aitab vähendada kliimamuutuste riske.
Väljakutsed:
- Tuumajäätmed: Tuumareaktsiooni tulemusena tekivad radioaktiivsed jäätmed, mis tuleb ohutult ladustada.
- Tuumakatastroofi risk: Kuigi väga haruldane, võib tuumaõnnetus põhjustada katastroofilisi tagajärgi nii keskkonnale kui ka inimeludele.
- Kõrged alginvesteeringud: Tuumajaamade ehitamine ja hooldamine on äärmiselt kallis ning nõuab pikaajalisi investeeringuid.
Kokkuvõttes on tuumaenergia võimas ja tõhus energiaallikas, kuid sellega kaasnevad tõsised väljakutsed, mis nõuavad hoolikat juhtimist ja põhjalikku ohutust tagavaid meetmeid.
Taastuvenergia jaamad: Tuule-, Päikese- ja Hüdroelektrijaamad
Taastuvenergia jaamad on võtmetähtsusega keskkonnasõbraliku ja kestliku energiatoomise tagamisel. Peamised taastuvenergia jaamad hõlmavad tuuleelektrijaamu, päikeseelektrijaamu ja hüdroelektrijaamu. Igal neist on oma unikaalsed omadused ja tööpõhimõtted, mis muudavad need sobivaks erinevatesse keskkondadesse ja energia tootmise vajadusteks.
Tuuleelektrijaamad

Tuuleelektrijaamad kasutavad tuule kineetilist energiat elektrienergia tootmiseks. Tuuleturbiinid, mis on tavaliselt koondatud tuuleparkidesse, on paigaldatud kohtadesse, kus on püsivad ja tugevad tuuled, näiteks rannikualad ja avameri.
- Tööprotsess: Tuuleturbiini labad, mis on kinnitatud rootorile, hakkavad tuule mõjul pöörlema. See mehaaniline liikumine käivitab generaatori, mis muundab tuule kineetilise energia elektrienergiaks.
- Kasutusala: Tuuleelektrijaamu kasutatakse laialdaselt piirkondades, kus on soodsad tuuletingimused. Need võivad olla nii maismaal kui ka merel paiknevad tuulepargid.
- Väljakutsed: Peamine väljakutse on tuule ebastabiilsus – kui tuult ei ole, ei toimu ka elektritootmist. Samuti võivad tuuleelektrijaamad mõjutada maastikku ja kohalikke ökosüsteeme.
Päikeseelektrijaamad


Päikeseelektrijaamad kasutavad päikesevalgust elektri tootmiseks. Päikesepargid koosnevad suurtest päikesepaneelide väljadest või kontsentreeritud päikeseenergia süsteemidest, mis koondavad päikesevalgust.
- Tööprotsess: Päikesepaneelid, mis põhinevad fotogalvaanilisel efektil, muundavad päikesevalguse elektrivooluks. Alternatiivina kasutatakse päikeseenergia kontsentreerimissüsteeme, mis koondavad päikesevalguse väikesele alale, tootes soojust, mis tekitab auru turbiinide käitamiseks.
- Kasutusala: Päikeseelektrijaamad on tõhusad piirkondades, kus on palju päikesepaistelisi päevi, näiteks kõrbetes või troopilistes piirkondades. Need võivad olla väikese mahuga kohalikud süsteemid või suured päikesepargid.
- Väljakutsed: Päikeseenergia tootmine on piiratud päevavalgusega ja võib olla vähenenud pilves ilmaga. Öösel ei toimu elektritootmist, mistõttu on vaja tõhusaid energiasalvestussüsteeme.
Hüdroelektrijaamad

Hüdroelektrijaamad kasutavad voolava vee liikumist elektri tootmiseks. Need jaamad on tavaliselt ehitatud jõgedele, kus tammi abil juhitakse vee voolu turbiinidele.
- Tööprotsess: Tammide abil luuakse veehoidlad, kust juhitakse vett läbi turbiinide. Vee liikumine paneb turbiinid pöörlema, mis omakorda käitab generaatori, tootes elektrienergiat.
- Kasutusala: Hüdroelektrijaamad on tõhusad ja usaldusväärsed energiaallikad piirkondades, kus on suurte jõgede süsteemid. Neid kasutatakse peamiselt baseload (põhikoormuse) energia tootmiseks, kuna nad suudavad toota elektrit järjepidevalt.
- Väljakutsed: Hüdroelektrijaamad võivad oluliselt mõjutada kohalikke ökosüsteeme, sealhulgas kalade rännet ja elupaiku. Lisaks on nende ehitamine kulukas ja keskkonnale suur koormus, eriti suurte tammide puhul.
Kokkuvõttes on tuule-, päikese- ja hüdroelektrijaamad võtmetähtsusega taastuvenergia lahendused, mis pakuvad puhtamat alternatiivi fossiilkütustel põhinevale elektritootmisele. Kuigi igal jaamatüübil on oma eelised ja väljakutsed, on nende ühiseks eesmärgiks kestliku ja keskkonnasõbraliku elektritootmise tagamine. Nende jaamade laiem kasutuselevõtt on hädavajalik, et täita tulevikus kasvavat energiavajadust ja samal ajal vähendada meie ökoloogilist jalajälge.
Energia tootmine hõlmab protsesse, mille käigus erinevatest energiaallikatest muundatakse energia elektrivooluks. Peamised energiaallikad hõlmavad:
- Fossiilkütused (nagu kivisüsi, nafta ja maagaas): Need on traditsioonilised energiaallikad, kus põletamisel vabanev soojusenergia muundatakse elektriks auruturbiinide abil.
- Tuumaenergia: Tuumaelektrijaamades kasutatav tehnoloogia põhineb aatomituumade lõhustumisel, mille käigus vabanev soojusenergia kasutatakse vee aurustamiseks ja auruturbiinide käivitamiseks.
- Taastuvenergia: Sellised allikad nagu tuule-, päikese- ja hüdroenergia on üha populaarsemad, kuna need on puhtad ja keskkonnasõbralikud. Tuulepargid ja päikesepargid toodavad energiat, muutes tuule või päikesevalguse elektrienergiaks. Hüdroelektrijaamad kasutavad voolavat vett elektri tootmiseks.
- Biomass ja geotermiline energia: Need allikad, kuigi vähem levinud, on samuti olulised. Biomassi puhul kasutatakse orgaanilist materjali (nt puiduhake, põllumajanduslikud jäätmed), samas kui geotermiline energia kasutab Maa sisemuses salvestunud soojust.
Energia ülekanne
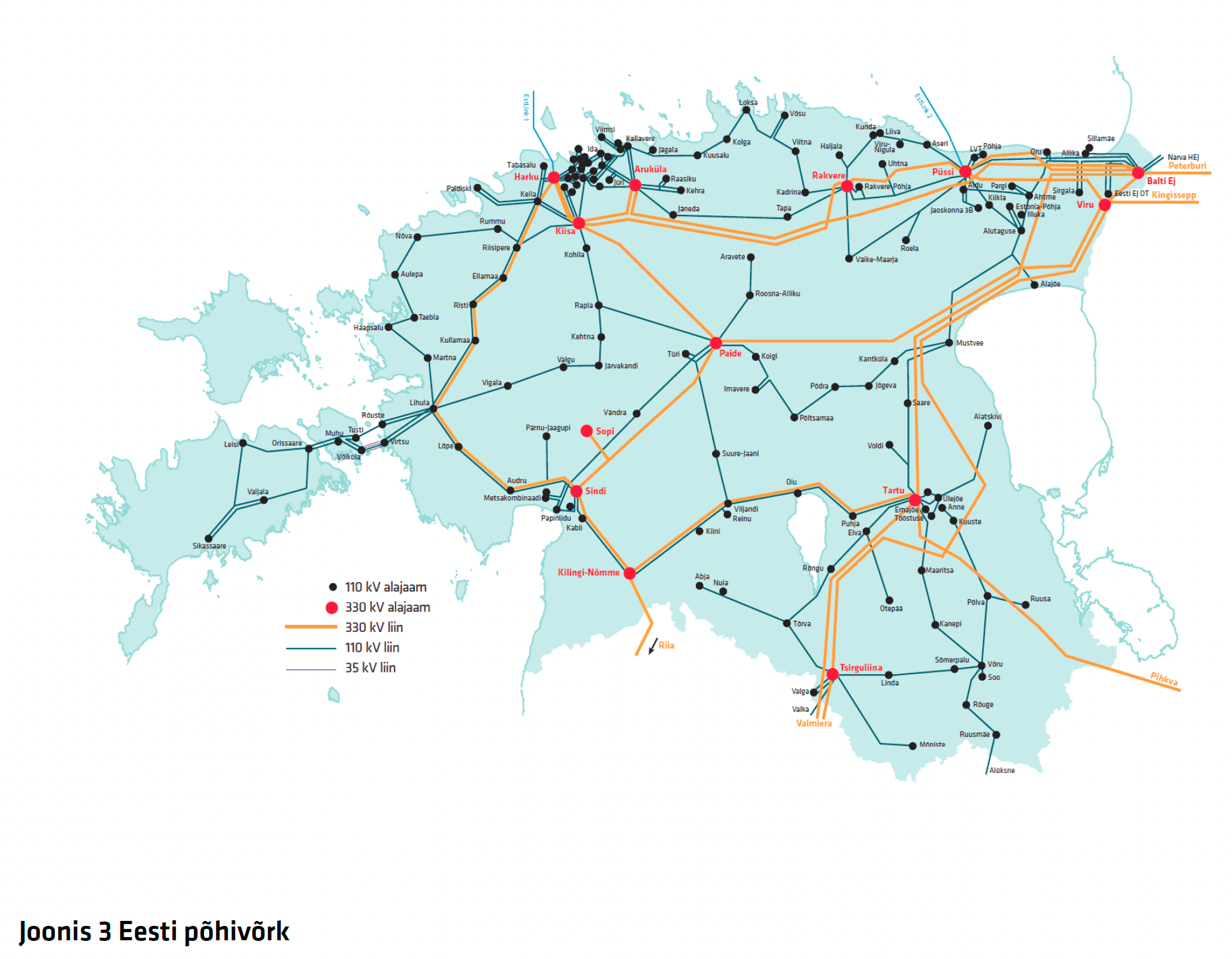
Pärast energia tootmist tuleb see edastada tootmiskohtadest tarbijateni. Selleks kasutatakse elektrivõrke, mis koosnevad ülekandeliinidest, alajaamadest ja jaotussüsteemidest. Ülekandeliinide kaudu liigub elektrienergia suurtelt elektrijaamadelt alajaamadesse, kus pinge alandatakse sobivale tasemele, et see oleks turvaline ja kasutatav tarbijate poolt.

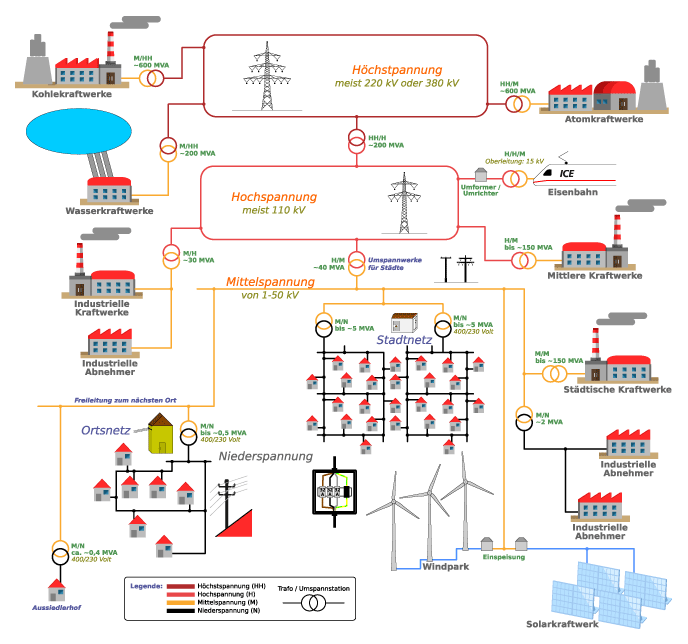
- Ülekandeliinid: Kõrgepingeliinid edastavad elektrienergiat pikki vahemaid, sageli üle kogu riigi või isegi riikide vahel. Need liinid töötavad kõrge pingega (tavaliselt vahemikus 110 kV kuni 765 kV), et vähendada energiakadu.
- Alajaamad: Alajaamades alandatakse kõrgepingeline elektrienergia madalamale pingele, et see oleks sobiv jaotamiseks kohalikus elektrivõrgus ja lõpuks tarbijate kasutusse.
- Jaotusvõrgud: Jaotusvõrgud viivad energia lõplikult tarbijateni, sealhulgas kodudesse, kontoritesse ja tööstustesse. Siin toimub pinge edasine alandamine, et seadmed ja masinad saaksid elektrienergiat ohutult kasutada.
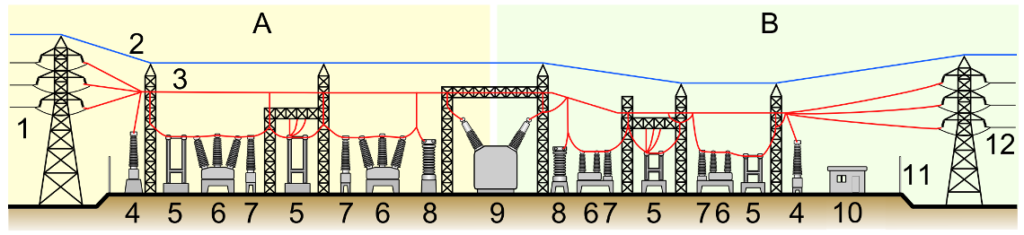
Välisalajaama osad ja elemendid: A – ülempingeosa; B – alampingeosa
1 – sisenev kõrgepingeliin; 2 – maandusjuht; 3 – ülempingejaotla; 4 – pingemõõtetrafo; 5 – lahklüliti (lülitamiseks vooluvabas olekus); 6 – võimsuslüliti (koormusvoolulülitamiseks); 7 – voolumõõtetrafo; 8 – piksekaitse; 9 – jõutrafo; 10 – juhtimiskeskus; 11 – turvatara; 12 – väljuvad alampingeliinid (alampingejaotla)
Väljakutsed ja tulevikutrendid
Energia tootmine ja ülekanne seisavad silmitsi mitmete väljakutsetega, sealhulgas vananev taristu, kasvav energiavajadus ning keskkonnakaitse ja kestlikkuse küsimused. Samal ajal on käimas revolutsioonilised muudatused, nagu nutikad elektrivõrgud, mis kasutavad infotehnoloogiat ja andmeanalüüsi energiakasutuse optimeerimiseks ning taastuvenergiaallikate suurem integreerimine, et vähendada sõltuvust fossiilkütustest.
Tuleviku energiasüsteemid muutuvad tõenäoliselt üha hajutatumaks, kus väiksemad tootmisüksused (nt kodused päikesepaneelid ja kohalikud tuulegeneraatorid) mängivad suuremat rolli ning energiasalvestustehnoloogiad (nt akud) aitavad stabiliseerida elektrivõrke ja tagada katkematu energiatootmise ka siis, kui taastuvenergia allikad ei ole kättesaadavad.
Kokkuvõttes on energia tootmine ja ülekanne kriitilise tähtsusega, tagades elektrienergia kättesaadavuse ja usaldusväärsuse tänapäeva maailmas ning kujundades meie tulevikku puhtama ja jätkusuutlikuma energiamajanduse suunas.
Rakendusalad
Elektrotehnika ja elektroonika rakendusvaldkonnad on väga laiad. Siin on mõned olulisemad näited:
- Energeetika: Elektrivõrkude projekteerimine ja haldamine, taastuvenergia lahenduste arendamine, energia salvestamise tehnoloogiad.
- Telekommunikatsioon: Juhtmevabad sidelahendused, mobiilsidevõrgud, interneti infrastruktuur, satelliitside.
- Arvutustehnika: Mikroprotsessorid, andmetöötlussüsteemid, pilvearvutus.
- Meditsiin: Meditsiiniseadmete ja -instrumentide arendamine, näiteks EKG-aparaadid ja meditsiinilised pildistamisseadmed.
- Autotööstus: Elektriautode jõuelektroonika, nutikad juhtimissüsteemid, ohutusseadmed.
- Kosmosetehnika: Satelliitide juhtimissüsteemid, kosmosesondid, Maa kaugseire süsteemid.
Rakendusalade näited
Skeemid, mis illustreerivad elektrotehnika ja elektroonika erinevate rakendusalade näiteid, nagu energiatootmine, telekommunikatsioon ja meditsiin.
1.2 Õppe-eesmärgid
Kursuse eesmärk on pakkuda õpilastele tugevat alust elektrotehnika ja elektroonika põhiprintsiipides, mis on vajalikud edasiseks õppimiseks ja praktiliseks tööks nendes valdkondades. Kursuse lõpuks peaksid õpilased olema suutnud:
- Mõista elektri põhialuseid ja komponente:
- Selgitada elektrivoolu, pinge ja takistuse põhiprintsiipe.Erinevuste ja rakenduste mõistmine alalisvoolu ja vahelduvvoolu vahel.
- Kasutada Ohmi seadust voolu, pinge ja takistuse arvutamiseks lihtsates vooluringides.
- Omandada elektrotehnika oluliste terminite ja seaduste põhjalik arusaam, sealhulgas:
- Coulomb’i seadus, mis kirjeldab laetud osakeste vastastikust mõju,
- Kirchhoffi seadused, mis reguleerivad voolude ja pingete jaotust vooluringides,
- Joule-Lenzi seadus, mis selgitab elektrivoolu kaudu eralduvat soojust.
- Neid teadmisi rakendatakse elektriahelate analüüsimisel ja lahendamisel, et mõista voolu ja pinge jaotust erinevates komponentides ja ahelates.
- Tuvastada elektriskeemides kasutatavaid sümboleid, nagu takistid, kondensaatorid, dioodid ja transistorid.
- Koostada ning analüüsida lihtsaid vooluringe, kasutades elektriskeeme ja vastavaid komponente.
- Lugeda ja koostada lihtsaid elektriskeeme:
- Tunda ära elektriskeemi sümboleid, nagu takistid, kondensaatorid, dioodid ja transistorid.
- Koostada ja analüüsida lihtsaid vooluringe, kasutades elektriskeeme.
- Mõista pooljuhtide ja elektroonika põhialuseid:
- Kirjeldada pooljuhtide tööpõhimõtteid ja nende rolli elektroonikas.
- Tunda ja selgitada dioodide, transistoride ja teiste pooljuhtseadmete tööd ja rakendusi.
- Töötada laboriseadmete ja mõõteriistadega:
- Kasutada ohutult ja tõhusalt multimeetreid, osillograafe ja teisi mõõtevahendeid.
- Teha praktilisi katseid, et kontrollida ja kinnitada teoreetilisi teadmisi.
- Analüüsida ja lahendada praktilisi probleeme:
- Rakendada kursusel omandatud teadmisi reaalsete probleemide lahendamiseks.
- Analüüsida vooluringide tööd ja tuvastada võimalikke probleeme.
- Mõista kaasaegse elektroonika rakendusi:
- Tunda ära elektroonika põhilised rakendused erinevates tööstus- ja tarbijaseadmetes.
- Mõista elektroonika rolli tulevikutehnoloogiates, nagu IoT, nutikad võrgud ja tehisintellektiga süsteemid.
Need õppe-eesmärgid on suunatud selleks, et õpilased saaksid omandada vajalikud teadmised ja oskused, mis võimaldavad neil edukalt osaleda edasises õppes või tööelus elektrotehnika ja elektroonika valdkonnas.
2. Põhimõisted
Selles peatükis käsitletakse elektrotehnika ja elektroonika kolme olulist põhimõistet: elektrivoolu, pinget ja takistust. Samuti käsitletakse Ohmi seadust, mis seob need kolm mõistet omavahel ja on aluseks elektriliste vooluringide analüüsile.
2.1 Elektrivool
Definitsioon:
Elektrivool on laetud osakeste (peamiselt elektronide) liikumine juhtmes või muus juhtivas keskkonnas. Elektrivool tekib, kui laetud osakesed liiguvad ühes suunas, mida põhjustab pinge. Elektrivoolu tugevust mõõdetakse amprites (A), mis näitab, kui palju laengut (kulonites, C) läbib juhti teatud ajaühikus (sekundites, s).

Tähis ja ühik:
- Tähis: I
- Ühik: Amper (A)
Matemaatiline seos:
![]()
kus:
- I on voolutugevus, mõõdetakse amprites (A),
- Q on laeng, mõõdetakse kulonites (C),
- t on aeg, mille jooksul see laeng juhti läbib, mõõdetakse sekundites (s).
2.2 Pinge
Pinge on elektriväli, mis paneb laetud osakesed liikuma juhtmes. See tekib, kui juhtme kahe punkti vahel on potentsiaalne erinevus. Pinge mõõdetakse voltides (V) ja tähistatakse U või V. Matemaatiliselt seostub pinge tööga (W) ja laenguga (Q) järgmise valemiga:
Pinge valem:
![]()
Kus:
- U on pinge voltides (V),
- W on töö džaulides (J),
- Q on laeng kulonites (C).
Ilma pingeta ei saa elektrivool juhtmes liikuda, sest just pinge tekitab voolu. Mjau!
2.3 Takistus
Definitsioon:
Takistus on omadus, mis piirab voolu läbimist juhtmes või komponendis. Takistus tekib seetõttu, et juhtme sees olevad aatomid takistavad elektronide liikumist. Takistust mõõdetakse oomides (Ω) ja see sõltub materjali tüübist, juhtme pikkusest ja ristlõike pindalast.
Tähis ja ühik:

- Tähis: R
- Ühik: Oom (Ω)
Matemaatiline seos:
![]()
kus:
- R on takistus, mõõdetakse oomides (Ω),
- U on pinge, mõõdetakse voltides (V),
- I on voolutugevus, mõõdetakse amprites (A).
Juhi takistuse arvutamine on oluline osa elektriahela analüüsist. Takistust mõõdetakse oomides (Ω) ja see sõltub juhi pikkusest, ristlõikepindalast, materjalist ning temperatuurist. Juhi takistust saab arvutada järgmise valemi abil:
Takistuse valem:
![]()
Kus:
- R on juhi takistus (oomides, Ω),
- ρ (rho) on materjali eritakistus ehk spetsiifiline takistus (oom-meetrites, Ω·m),
- L on juhi pikkus (meetrites, m),
- A on juhi ristlõikepindala (ruutmeetrites, m²).
Eritakistus (ρ):
Eritakistus on materjali omadus ja see näitab, kui palju takistab materjal elektrivoolu liikumist. Eritakistus sõltub materjalist ja temperatuurist. Näiteks vask on hea juht ja selle eritakistus on väiksem kui raual või alumiiniumil.
Ristlõikepindala (A):
Juhi ristlõikepindala on pindala, mis on risti voolu liikumise suunaga. Tavaliselt on juhtmed silindrilise kujuga, nii et ristlõikepindala saab arvutada valemiga:
![]()
Kus:
- r on juhi raadius (meetrites).
Kui juhi läbimõõt (d) on teada, siis:
![]()
Näide:
Oletame, et teil on 10 meetri pikkune vaskjuhe, mille läbimõõt on 2 mm (0,002 m). Vaskjuhtme eritakistus on umbes 1,68 × 10⁻⁸ Ω·m.
- Arvutage ristlõikepindala:
![Rendered by QuickLaTeX.com \[A = \frac{\pi \times (0,002 m)^2}{4} = 3,14 \times 10^{-6} m^2\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-50e412e6a83357b631fdf60cee323c52_l3.png)
- Arvutage takistus:
![Rendered by QuickLaTeX.com \[R = 1,68 \times 10^{-8} \times \frac{10 m}{3,14 \times 10^{-6} m^2} = 0,0535 \Omega\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-5d5ad39edb0aac59beb569c835066087_l3.png)
Selle valemi abil saate arvutada takistuse mis tahes juhtiva materjali puhul, kui materjali eritakistus ja juhi geomeetrilised omadused on teada.
2.4 Ohmi seadus
Seaduse sõnastus:
Ohmi seadus seob omavahel pinge (U), voolutugevuse (I) ja takistuse (R) elektrilises vooluringis. Seaduse kohaselt on voolutugevus juhtmes võrdeline pinge suurusega ja pöördvõrdeline takistuse suurusega.
Matemaatiline väljend:
![]()
![]()
![]()
kus:
- I on voolutugevus (A),
- U on pinge (V),
- R on takistus (Ω).
Rakendused:
- Voolu arvutamine: Kui on teada pinge ja takistus, saab Ohmi seaduse abil arvutada voolutugevuse vooluringis.
![Rendered by QuickLaTeX.com \[ I = \frac{U}{R} \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-d9641d8e327621972fff932c8dab44ed_l3.png)
- Pinge arvutamine: Kui on teada voolutugevus ja takistus, saab arvutada pinge.
![Rendered by QuickLaTeX.com \[ U = I \times R \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-80904397daa4892c7ae644aa8bef0d84_l3.png)
- Takistuse arvutamine: Kui on teada pinge ja voolutugevus, saab arvutada takistuse.
![Rendered by QuickLaTeX.com \[ R = \frac{U}{I} \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-f924aade1f7d2243034b59324349fe54_l3.png)
Näide:
Oletame, et vooluringis on takisti, mille takistus on 4 Ω, ja sellele rakendatakse 12 V pinget. Voolutugevuse leidmiseks kasutame Ohmi seadust:
![]()
See tähendab, et voolutugevus juhis on 3 amprit.
Ohmi seadus on fundamentaalne tööriist elektriliste vooluringide analüüsis ja disainis, võimaldades inseneridel ja tehnikutel arvutada ja planeerida, kuidas erinevad elektrilised komponendid koos töötavad.
Elektriahelate lahendamine ja põhiseadused
Selles peatükis käsitleme elektrotehnika olulisi põhiseadusi, nagu Coulomb’i seadus, Kirchhoffi seadused ja Joule-Lenzi seadus, mis on kriitilise tähtsusega elektriahelate analüüsimisel ja lahendamisel. Esitame need seadused üksikasjalikult koos näidetega, et selgitada, kuidas neid seadusi praktikas rakendada.
2.5. Coulomb’i seadus

Seaduse sõnastus:
Coulomb’i seadus kirjeldab jõudu, mis toimib kahe laetud keha vahel. Jõud on võrdeline laengute suurusega ja pöördvõrdeline nendevahelise kauguse ruuduga. Seda seadust kasutatakse laetud osakeste vahelise elektrilise jõu arvutamiseks.
Matemaatiline seos:
![]()
kus:
- F on jõud, mõõdetakse newtonites (N),
- k on Coulomb’i konstant
,![Rendered by QuickLaTeX.com \[((8.99 \times 10^9 \, \text{N} \cdot \text{m}^2 / \text{C}^2))\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-07179fa462d9c7c2308aff1fae4d98d8_l3.png)
- q1 ja q2 on laengud kulonites (C),
- r on laengutevaheline kaugus meetrites (m).
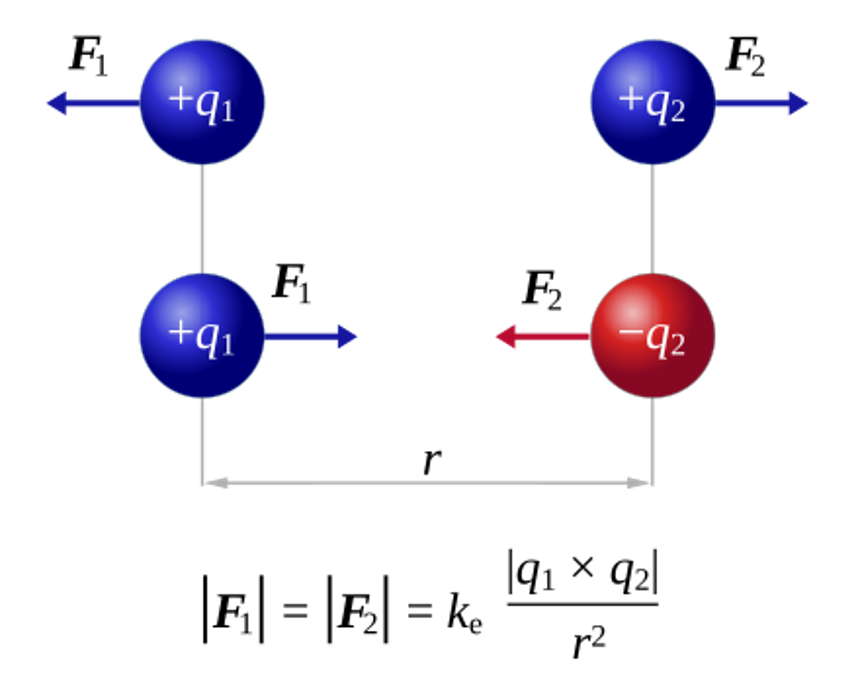
Näide:
Kaks punkti laengut,
![]()
, paiknevad 1 meetri kaugusel teineteisest. Leiame nende laengute vahelise jõu.
![]()
Tulemus on
![]()
mis tähendab, et jõud on tõmbav, kuna ühe laengu märgiks on positiivne ja teise oma negatiivne.
Rakendused:
- Coulomb’i seadust kasutatakse laetud kehade vaheliste jõudude arvutamiseks, näiteks füüsikas või inseneriteadustes, et arvutada elektromagnetiliste komponentide mõju.
2.6. Kirchhoffi seadused
Kirchhoffi seadused on elektrivoolude ja pingete jaotumise kohta elektrivooluringides kehtivad kaks olulist reeglit. Need seadused aitavad lahendada keerukamaid vooluringe, kus on mitu hargnemist ja mitmesuguseid komponente.
Kirchhoffi vooluseadus (KVS)

Seaduse sõnastus:
Kirchhoffi vooluseadus (I seadus) ütleb, et voolude summa igas vooluringi hargnemiskohas on null. See tähendab, et kõikide sisenevate voolude summa peab olema võrdne väljuvate voolude summaga.
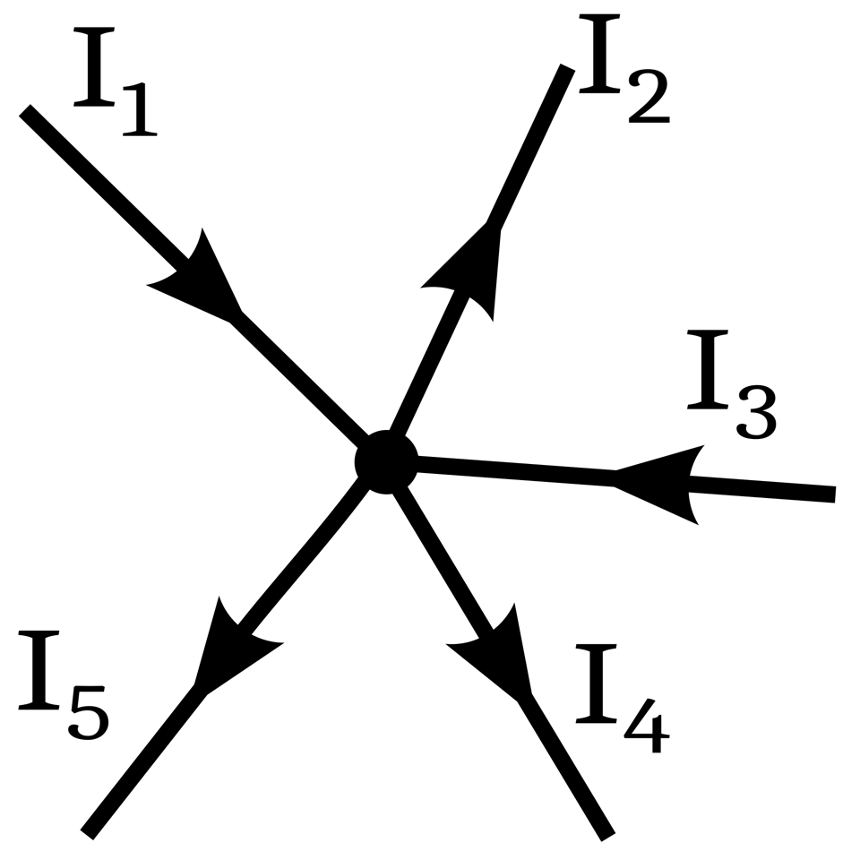
Matemaatiline seos:
![]()
Näide:
Vaadake vooluringi, kus vooluallikas jagab voolu kolmeks haruks. Hargnemiskohal on sisenev vool
![]()
ja väljuvad voolud on
![]()
Leiame kolmanda haru voolu (I_4).
![]()
![]()
![]()
Seega on kolmanda haru vool
![]()
Rakendused:
- Kirchhoffi vooluseadust kasutatakse hargnenud vooluringide arvutamiseks, näiteks vooluahelate tasakaalu ja koormusjaotuse leidmisel.
Ülesanne – Kirchhoffi I seadus
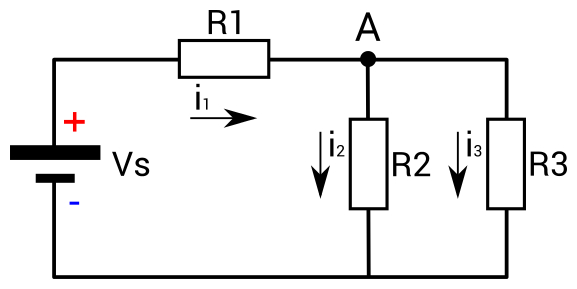
Olgu ülesandeks leida joonisel toodud ahela voolutugevused 






Vool läbib ahelat kahte kontuuri pidi – läbi takistite 




Kirchhoffi teise seaduse kohaselt on kontuuri läbivate pingelangude summa võrdne nulliga. Et antud skeemis on pingeallikast lähtuvalt kaks kontuuri, saame kirjutada:

Koostame võrrandisüsteemi

Seda võrrandisüsteemi lahendades saame 
Kontrollime vastavust Kirchhoffi esimesele seadusele:
Ülesanne võetud: https://et.wikipedia.org/wiki/Kirchhoffi_seadused
Kirchhoffi pingeseadus (KPS)
Seaduse sõnastus:
Kirchhoffi pingeseadus (II seadus) ütleb, et suletud vooluringis on kõigi pingelangude summa võrdne pingeallikate summaga. See tähendab, et vooluringi igas suletud silmuses peab kogu pingete summa olema null.
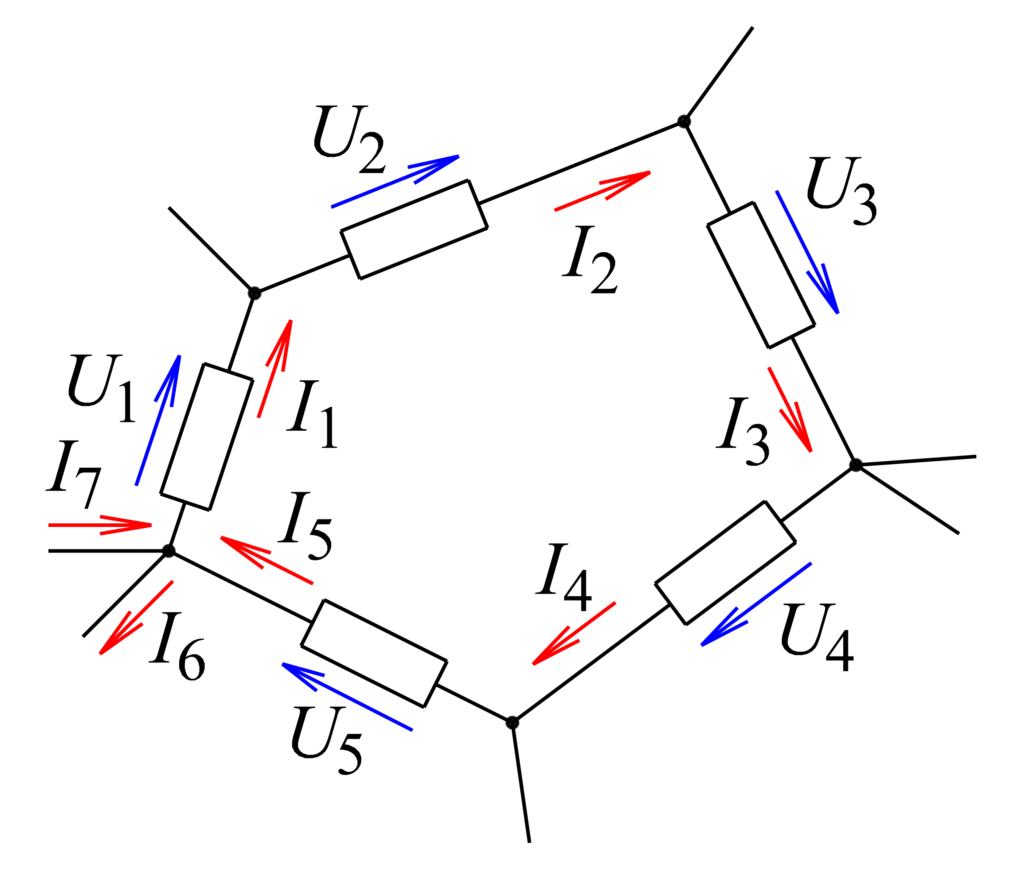
Matemaatiline seos:
![]()
Näide:
Vaatame suletud vooluringi, kus pingeallikas annab ![]() ja vooluringis on kaks takistit:
ja vooluringis on kaks takistit:
![]()
Leiame voolu vooluringis.
Kasutame Ohmi seadust:
![]()
- Pingeallikas annab kokku
.![Rendered by QuickLaTeX.com \[(12 \, \text{V})\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-e6e30309712954799ff1f11a00b4da92_l3.png)
- Pingelangud on:
.![Rendered by QuickLaTeX.com \[(U_1 = I \times 4 \, \Omega) ja (U_2 = I \times 2 \, \Omega)\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-3d56aade08a4f0fa47f72259505f0c0a_l3.png)
Vooluringis peab pinge olema tasakaalus:
![]()
![]()
![]()
Seega on vool vooluringis ![]() .
.
Rakendused:
- Kirchhoffi pingeseadust kasutatakse vooluringide analüüsimiseks ja pingejaotuste leidmiseks keerukates elektrivõrkudes, näiteks arvuti toiteplokkides ja auto elektrisüsteemides.
Ülesanne Kirchhoffi II seadus
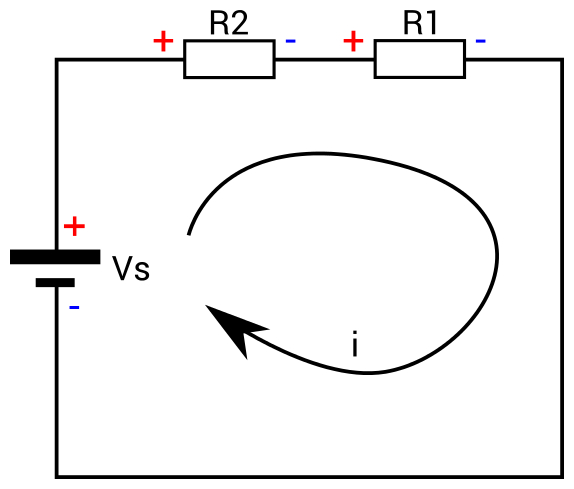
Olgu ülesandeks leida pingelangud joonisel toodud skeemi takistitel 




Edasi lepitakse kokku, et takistil tekib voolu liikumise suunas pingelang, ehk takisti ühel pool (pingeallika positiivsele klemmile lähemal) on pinge kõrgem kui teisel. Sama kokkulepe kehtib kõikidele kontuuris olevatele takistitele. Jällegi, seadus töötab ka vastupidise kokkuleppe korral.
Nüüd on ülesande lahendamiseks kõik suurused teada ja kokkulepped joonisele 2 kantud. Lähtudes definitsioonist 

Kirjutame eelmise seose lähtudes Oomi seadusest järgmiselt
Selle võrrandi lahendamiseks on kõik suurused teada, seega
Teades kontuuri läbivat voolu, saame arvutada pingelangud:

Kontrollime vastavust Kirchhoffi teisele seadusele: 
Ülesanne võetud: https://et.wikipedia.org/wiki/Kirchhoffi_seadused
2.7. Joule-Lenzi seadus

Seaduse sõnastus:
Joule-Lenzi seadus ütleb, et elektrivoolu käigus arenev soojusenergia on võrdeline voolutugevuse ruudu, takistuse ja ajaga, mille jooksul vool läbi takisti läbib.
Matemaatiline seos:
![]()
kus:
- Q on soojushulk, mõõdetakse džaulides (J),
- I on voolutugevus amprites (A),
- R on takistus oomides
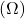 ,
, - t on aeg sekundites (s).
Näide:
Oletame, et elektriline soojenduskeha töötab voolutugevusega ![]() , ja selle takistus on
, ja selle takistus on ![]() . Arvutame, kui palju soojust eraldub (60) sekundi jooksul.
. Arvutame, kui palju soojust eraldub (60) sekundi jooksul.
![]()
![]()
![]()
Seega eraldub soojenduskehas (15 000) džauli soojust.
Rakendused:
- Joule-Lenzi seadust kasutatakse elektriliste kütteseadmete disainimisel ja soojuskao arvutamisel elektrijuhtmetes ning seadmete ohutuse tagamisel.
See peatükk annab ülevaate Coulomb’i, Kirchhoffi ja Joule-Lenzi seadustest ning selgitab, kuidas neid kasutada elektrivooluringide analüüsimisel ja lahendamisel. Seaduste rakenduste mõistmine aitab õpilastel lahendada praktilisi ülesandeid ja töötada välja tõhusaid elektriahelaid.
2.8. Võimsus
Võimsuse arvutamine alalisvoolu (DC) ja vahelduvvoolu (AC) korral toimub erinevate meetoditega, kuna nende voolutüüpide omadused on erinevad. Allpool on selgitatud, kuidas võimsust arvutada mõlemas voolutüübis.

Alalisvool (DC)
Alalisvoolus on pinge ja vool konstantne, seega võimsuse arvutamine on suhteliselt lihtne.
Valem:
![]()
Kus:
- P on võimsus (vattides, W),
- U on pinge (voldis, V),
- I on voolutugevus (amprites, A).
Näide:
Kui teil on alalisvooluahel, kus pinge on 12 V ja voolutugevus 2 A, siis võimsus on:
![]()
3. Elektromagnetism
Elektromagnetism on füüsika haru, mis uurib elektrivoolu ja magnetvälja omavahelist seost. See on elektrotehnika ja elektroonika keskne osa, sest paljud seadmed ja tehnoloogiad põhinevad elektromagnetilistel põhimõtetel. Selles peatükis käsitleme magnetvälja ja elektrivoolu vahelist suhet, sealhulgas Lorentzi jõudu ja elektromagnetilist induktsiooni, ning arutame transformaatorite tööpõhimõtteid ja nende rakendusi.

3.1 Magnetvälja ja elektrivoolu suhe
Magnetväli ja elektrivool:
Kui elektrivool liigub läbi juhi (näiteks traadi), tekitab see enda ümber magnetvälja. See magnetväli ümbritseb juhti kontsentriliste rõngastena, mille suund sõltub voolu suunast. Seda nähtust kirjeldab Ampère’i seadus.
Lorentzi jõud:
Lorentzi jõud on jõud, mida magnetväli avaldab liikuvale laetud osakesele, näiteks elektronile. Kui laetud osake liigub läbi magnetvälja, mõjub sellele jõud, mis on risti nii magnetvälja suuna kui ka osakese liikumise suunaga. Lorentzi jõud on oluline mõiste elektromagnetilistes seadmetes, nagu elektrimootorid ja generaatorid.
Matemaatiline seos:
Lorentzi jõud (F) on määratud järgmise valemiga:
![]()
kus:
- F on jõud, mõõdetakse newtonites (N),
- q on osakese laeng, mõõdetakse kulonites (C),
- v on osakese kiirus, mõõdetakse meetrites sekundis (m/s),
- B on magnetvälja induktsioon, mõõdetakse teslades (T),
- × sümbol tähistab vektorkorrutist, mis tähendab, et jõud on risti nii osakese liikumise kui ka magnetvälja suunaga.
Elektromagnetiline induktsioon:
Elektromagnetiline induktsioon on protsess, mille käigus muutuva magnetvälja mõjul tekib juhtmes elektrivool. Seda nähtust kirjeldab Faraday seadus, mis ütleb, et ajas muutuv magnetväli tekitab elektrivälja, mis indutseerib elektrivoolu juhtmes.
Matemaatiline seos:
Faraday elektromagnetilise induktsiooni seadus:
![]()
kus:
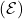 on indutseeritud elektromotoorjõud (emj), mõõdetakse voltides (V),
on indutseeritud elektromotoorjõud (emj), mõõdetakse voltides (V),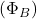 on magnetvoog, mõõdetakse veebrites
on magnetvoog, mõõdetakse veebrites 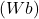 ,
,- t on aeg, mõõdetakse sekundites (s).
Magnetvoog ![]() on defineeritud kui magnetvälja tugevuse (B) ja pindala (A), mille kaudu väli läbib, korrutis:
on defineeritud kui magnetvälja tugevuse (B) ja pindala (A), mille kaudu väli läbib, korrutis:
![]()
kus:
- B on magnetvälja induktsioon, mõõdetakse teslades (T),
- A on pindala, mille kaudu magnetväli läbib, mõõdetakse ruutmeetrites (m²),
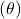 on nurk magnetvälja ja pinna normaali vahel.
on nurk magnetvälja ja pinna normaali vahel.
Parema ja vasaku käe reeglid on visuaalsed meetodid elektri- ja magnetväljade mõjude suuna määramiseks. Need on olulised elektromagnetismi mõistmiseks ja rakendamiseks erinevates tehnoloogiates.
Õppematerjal Gümnaasiumi füüsikast: Parema ja Vasaku Käe Reeglid
1. Sissejuhatus
- Eesmärk: Tutvustada parema ja vasaku käe reeglite põhimõtteid ja nende rakendusi elektromagnetismis.
- Taust: Elektrivool läbi juhtme tekitab selle ümber magnetvälja. Laetud osakese liikumine magnetväljas tekitab jõu, mis mõjutab osakese trajektoori.
2. Parema Käe Reegel
- Kirjeldus: Kasutatakse magnetvälja suuna määramiseks, mis on tekitatud elektrivoolu poolt, või jõu suuna määramiseks, mis mõjub laetud osakesele.
- Praktika:
- Magnetvälja suund: Siruta parema käe sõrmed välja ja suuna pöial voolu suunas läbi juhtme. Ülejäänud sõrmed näitavad magnetvälja suunda ümber juhtme.
- Jõud laetud osakesele: Kui positiiivne laeng liigub magnetväljas, suuna pöial voolu (liikumise) suunas, peopesa magnetvälja suunas ja sõrmed näitavad jõu suunda.
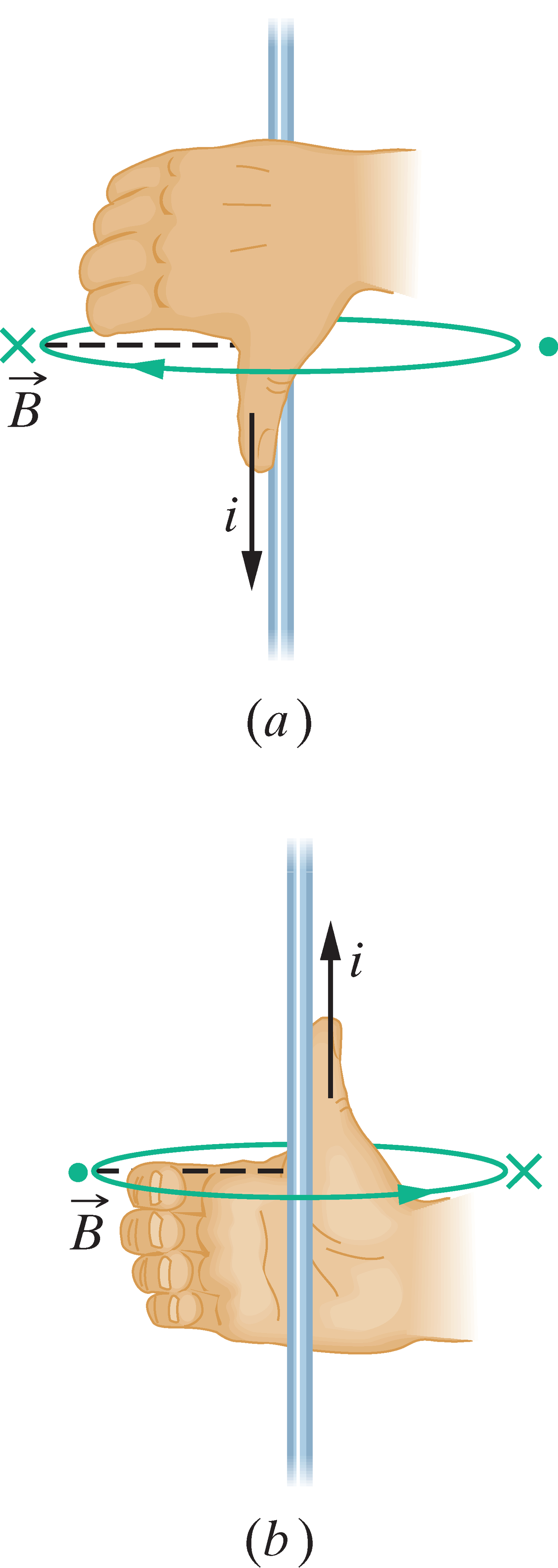
Parema käe reegel annab vooluga juhtme magnetvälja suuna
Parema käe reegel annab vooluga juhtme magnetvälja suuna. (a) Joonisel 29-2 kujutatud situatsioon külgvaates. Magnetväli →B suvalises juhtmest vasakul asetsevas punktis on risti radiaalse punktiirjoonega ja suunatud lehekülje tasandi sisse sõrmedega näidatud suunas, mida näitab ka tähis ×. (b) Kui muuta voolu suund vastupidiseks, siis on magnetväli →B suvalises juhtmest vasakul asetsevas punktis ikka suunatud risti radiaalse punktiirjoonega, kuid nüüd on see suunaga lehekülje tasandist välja, mida näitab ka tähis. (https://opik4.fyysika.ee/index.php/book/section/13308)
3. Vasaku Käe Reegel
- Kirjeldus: Kasutatakse mootoriefekti kirjeldamiseks, kus elektrivool ja magnetväli koosmõjul tekitavad jõu.
- Praktika:
- Aseta vasak käsi nii, et sõrmed osutavad magnetvälja suunas ja peopesa voolu suunas. Pöial näitab seejärel jõu suunda, mis mõjub juhtmele või laetud osakesele.
Joonisel on kujutatud kahte magnetit ja nende vahele asetatud vooluga juhtmelõiku. Veendu, et juhtmelõigule mõjuv magnetjõud on just selline, nagu joonisel kujutatud.
Lahendus
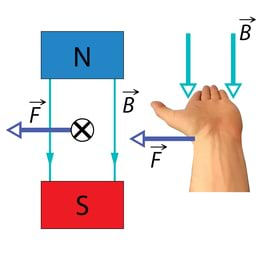
Joonisel on kujutatud ühe magneti põhjapoolus ja teise magneti lõunapoolus. Magnetvälja jõujoonte suund on järelikult ülevalt alla (põhjapooluselt lõunapoolusele). Juhtmelõik on magnetväljaga risti. Voolu suund on tähistatud ristiga juhtme ristlõik (https://opik4.fyysika.ee/index.php/book/section/13308).
4. Rakendused ja näited
- Elektrimootorid: Selgitatakse, kuidas elektrimootorid kasutavad vasaku käe reeglit pöörlemisjõu tekitamiseks.
- Generaatorid: Tutvustatakse, kuidas generaatorid kasutavad parema käe reeglit elektri tootmiseks mehaanilisest liikumisest.
5. Harjutused ja Katsetused
- Virtuaalne simulatsioon: Kasutajad saavad virtuaalselt simuleerida erinevaid stsenaariume, kus rakendatakse mõlemat käe reeglit.
- Füüsilised katsetused: Juhendid lihtsate katsete jaoks, mida saab läbi viia kodus või klassiruumis, et demonstreerida käe reeglite mõjusid.
6. Kokkuvõte
- Ülevaade õpitu olulisusest ja kuidas parema ja vasaku käe reegleid saab rakendada praktilistes olukordades tehnoloogia ja inseneriteaduste valdkonnas.
Selline struktureeritud lähenemine aitab õppijatel paremini mõista ja meelde jätta parema ja vasaku käe reeglite teoreetilisi aluseid ning praktikat.
3.2 Transformaatorid ja nende tööpõhimõte
Transformaatorite tööpõhimõte:
Trafo on seade, mis muundab vahelduvvoolu pinge ühest väärtusest teise, kasutades elektromagnetilise induktsiooni põhimõtet. Trafo koosneb kahest või enamast mähisest (esmane ja sekundaarne mähis), mis on paigutatud ümber ühise raudtuuma. Kui esmasele mähisele rakendatakse vahelduvvool, tekitab see muutuva magnetvälja, mis indutseerib pinge sekundaarse mähise kaudu.
Põhikomponendid:
- Primaarne mähis: Mähis, millele rakendatakse esialgne pinge.
- Sekundaarne mähis: Mähis, milles indutseeritakse pinge läbi elektromagnetilise induktsiooni.
- Raudtuum: Suunab magnetvoo läbi mähiste, suurendades induktsiooni efektiivsust.
Matemaatiline seos:
Transformaatori tööpõhimõtet kirjeldab järgnev valem, mis seob primaarse ja sekundaarse mähise pinged ning pöördeteguri:
![]()
kus:
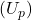 on primaarse mähise pinge, mõõdetakse voltides
on primaarse mähise pinge, mõõdetakse voltides 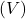 ,
,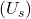 on sekundaarse mähise pinge, mõõdetakse voltides
on sekundaarse mähise pinge, mõõdetakse voltides 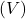 ,
,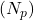 on primaarse mähise keerdude arv,
on primaarse mähise keerdude arv,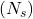 on sekundaarse mähise keerdude arv.
on sekundaarse mähise keerdude arv.
See tähendab, et pinge suhe on võrdeline mähiste keerdude arvuga. Kui sekundaarse mähise keerdude arv on suurem kui primaarse mähise oma, siis trafo suurendab pinget; vastasel juhul vähendab pinget.
Trafo tüübid:
- Tõstetrafo (Step-up transformer):
- Suurendab pinget esmase mähise madalast pingest kõrgemale pingele.
- Kasutatakse elektrienergia ülekandmisel pikkade vahemaade taha.
- Langetustrafo (Step-down transformer):
- Vähendab pinget kõrgemalt väärtuselt madalamale.
- Kasutatakse kodumajapidamistes ja tööstuses, et viia kõrge pinge elektrivõrgust madalamale kasutamiseks ohutule tasemele.
- Isolatsioonitrafo:
- Ülekanne toimub sama pingetaseme juures, kuid eraldab vooluahelaid elektriliselt.
- Kasutatakse ohutuse tagamiseks ja häirete vähendamiseks.
Kasutusalad:
- Elektrienergia ülekandmine: Trafo suurendab pinge elektrijaamades, et vähendada kaod elektrienergia ülekandmisel pikkade vahemaade taha. Sihtkohas langetatakse pinge tagasi tarbimiseks sobivale tasemele.
- Elektroonikaseadmed: Paljud elektroonikaseadmed kasutavad transformaatoreid toiteallikatena, et muundada vahelduvvoolu pinge vajalikule tasemele.
- Tööstuslikud rakendused: Trafo võimaldab juhtida erinevaid pingeid tööstuslikes seadmetes ja masinates.
Elektromagnetism on laiapõhjaline teadusharu, mis hõlmab elektri ja magnetismi vastastikmõjusid. Lorentzi jõud ja elektromagnetiline induktsioon on kaks peamist fenomeni, mis juhivad elektrivoolu ja magnetvälja vahelist seost. Trafo on praktiline seade, mis kasutab neid põhimõtteid elektrienergia tõhusaks ülekandmiseks ja muundamiseks. Nende kontseptsioonide mõistmine on oluline elektrotehnika ja elektroonika alal edasijõudmiseks ja rakenduste arendamiseks.
4. Elektriskeemid ja nende lugemine
Elektriskeemid on graafilised esitlused, mis näitavad, kuidas elektrilised komponendid on ühendatud vooluringis. Skeemide lugemine ja koostamine on elektrotehnika ja elektroonika alal põhioskuseks. Selles peatükis käsitleme erinevaid elektriskeemi sümboleid ja nende tähistusi ning selgitame lihtsate vooluringide koostamist ja lugemist.
4.1 Elektriskeemi sümbolid
Elektriskeemide lugemise hõlbustamiseks on igal komponendil oma standardiseeritud sümbol. Need sümbolid esindavad erinevaid komponente ja aitavad skeemi kiiresti mõista. Allpool on toodud mõned kõige sagedamini kasutatavad elektriskeemi sümbolid ja nende tähistused.
Takisti (Resistor)

- Sümbol:

- Kirjeldus: Takisti piirab voolu vooluringis. Seda kasutatakse, et kontrollida voolutugevust ja kaitsta teisi komponente liigse voolu eest.
- Tähis: R
- Ühik: Oom (Ω)
Takistite värvikood on süsteem, mida kasutatakse takistite väärtuse ja täpsuse tähistamiseks värviliste rõngaste abil. Enamikul takistitel on 4, 5 või 6 värvilist rõngast, mis tähistavad takistuse väärtust oomidena ja mõnikord ka takistuse täpsust (%).
Nelja rõngaga takisti värvikood
- Esimene rõngas: tähistab esimest numbrit.
- Teine rõngas: tähistab teist numbrit.
- Kolmas rõngas: tähistab kordajat (mitu nulli lisatakse).
- Neljas rõngas: tähistab täpsust (tolerants).
Näide:
- Värvikood: Pruun, Must, Punane, Kuldne.
- Pruun (1) = 1
- Must (0) = 0
- Punane (kordaja) = ×100
- Kuldne (täpsus) = ±5% Seega on takistuse väärtus: 10 × 100 = 1000 Ω ehk 1 kΩ ±5%.
Viie rõngaga takisti värvikood
- Esimene rõngas: tähistab esimest numbrit.
- Teine rõngas: tähistab teist numbrit.
- Kolmas rõngas: tähistab kolmandat numbrit.
- Neljas rõngas: kordaja.
- Viies rõngas: täpsus.
Kuue rõngaga takisti värvikood
- Sama, mis viie rõngaga süsteem, kuid kuues rõngas tähistab temperatuurikoefitsienti (PPM – parts per million), mis näitab, kuidas takisti väärtus muutub temperatuurimuutuste korral.
| Värv | 1. ja 2. numbrid | Kordaja (3. rõngas) | Täpsus (4. rõngas) |
|---|---|---|---|
| Must | 0 | ×1 | |
| Pruun | 1 | ×10 | ±1% |
| Punane | 2 | ×100 | ±2% |
| Oranž | 3 | ×1000 | |
| Kollane | 4 | ×10,000 | |
| Roheline | 5 | ×100,000 | ±0.5% |
| Sinine | 6 | ×1,000,000 | ±0.25% |
| Violettpunane | 7 | ×10,000,000 | ±0.1% |
| Hall | 8 | ×100,000,000 | ±0.05% |
| Valge | 9 | ×1,000,000,000 | |
| Kuldne | ×0.1 | ±5% | |
| Hõbedane | ×0.01 | ±10% |
Takistite värvikoodide süsteem on universaalne ja aitab kiiresti hinnata takistite väärtusi, mis on oluline elektrooniliste vooluahelate kavandamisel ja kasutamisel.
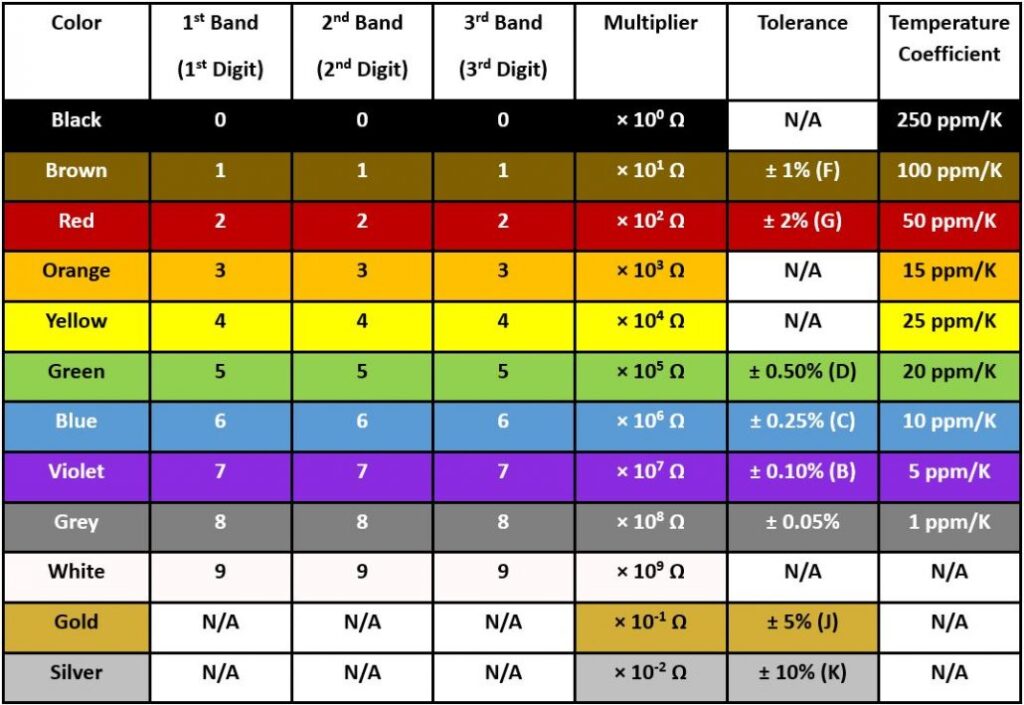
Takistid võivad olla kas lineaarsed või mittelineaarsed. Lineaartakisti korral on takistit läbiva voolu tugevus võrdeline rakendatud pingega. Seega on pingel ja takistit läbival voolul (i) lineaarne seos, mida graafikul kujutatakse sirgjoonena.
Mittelineaartakistite takistus sõltub oluliselt välistest mõjuritest nagu pinge (varistorid), temperatuur (termotakistid) või valguskiirgus (fototakistid).
Lineaartakisteid, mida kasutatakse kõige sagedamini, nimetatakse üldjuhul lihtsalt takistiteks.
Takistid on elektrotehnikas passiivsed komponendid, mis piiravad voolu ja jaotavad pinget elektriahelates. Need liigitatakse erinevatel alustel:
1. Materjali alusel:
- Süsiniktakistid: Valmistatud süsinikust või süsinikpulbrist koos sideainega. Need on odavad ja laialdaselt kasutatavad, kuid neil on kõrgem müratase ja piiratud täpsus.
- Metallkiletakistid: Valmistatud õhukese metallikihi pihustamisega isolatsioonimaterjalile. Neid iseloomustab suurem täpsus ja stabiilsus.
- Traattakistid: Tehtud isoleeritud juhtmetraadi mähkimisega südamiku ümber. Neid kasutatakse suurema võimsuse ja täpsuse jaoks.
2. Funktsiooni alusel:
- Fikseeritud takistid: Nende takistusväärtus on konstantne ja muutumatu. Neid kasutatakse voolu piiramiseks ja pingete jaotamiseks.
- Muudetavad takistid (potentsiomeetrid ja reostaadid): Neil on muutuv takistus, mida saab reguleerida vastavalt vajadusele. Potentsiomeetreid kasutatakse pinge jagajatena ja reostaate voolu reguleerimiseks.
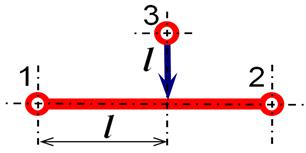
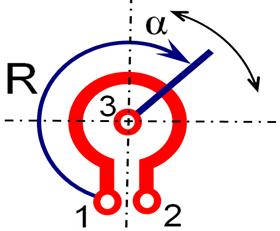
Kõige sagedamini kasutatakse lineaarseid reostaate. Nende takistustraat on mähitud karkassile kogu selle pikkuses ühtlase sammuga ühtse sektsioonina (joonis а). Liugurilt algavad kaks klemmi ja tekitavad kaks väljundtakistust R1 ja R2. Joonise b kõveratelt on näha, kuidas need takistused muutuvad. Tunnusjooned ![]() ja
ja ![]() on lineaarsed ning Rp on reostaadi kogutakistus.
on lineaarsed ning Rp on reostaadi kogutakistus.
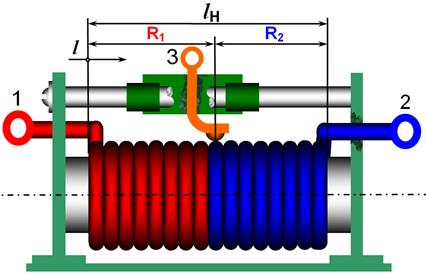
a
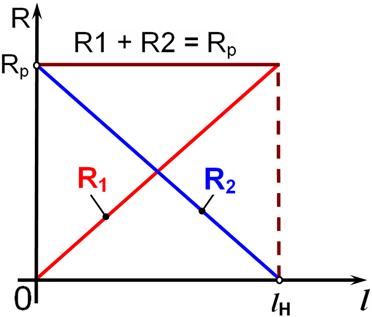
b
Toodetakse ka funktsionaalseid reostaate, mille tunnusjoon on tahtlikult mittelineaarne. Selle võib saavutada karkassi sobiva kujuga (joonis ), sobiva keerdude sammu valikuga või lineaarse reostaadi osade takistitega lühistamisega.
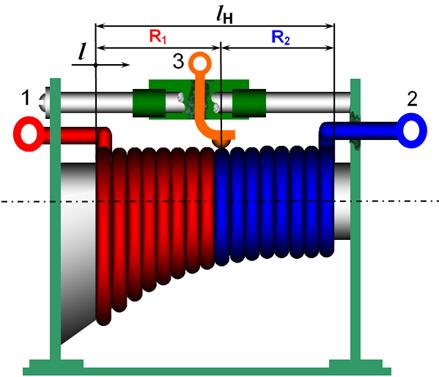
a
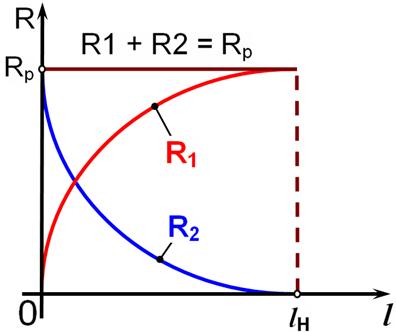
b
3. Võimsustaluvuse järgi:
- Madalvõimsustakistid: Tavaliselt alla 1 W. Kasutatakse ahelates, kus voolud on väiksed.
- Kõrgevõimsustakistid: Üle 1 W, sobivad rakendustesse, kus on vaja hajutada rohkem soojust.
4. Takistusväärtuse täpsuse järgi:
- Tavalised takistid: Neil on suurem lubatud hälve (±5% või ±10%).
- Täppistakistid: Neil on väiksem hälve, näiteks ±1% või isegi ±0.1%.
5. Temperatuurikoefitsiendi alusel:
- NTC (Negative Temperature Coefficient) takistid: Nende takistus väheneb temperatuuri tõustes.
- PTC (Positive Temperature Coefficient) takistid: Nende takistus suureneb temperatuuri tõustes.
Need liigid võimaldavad takisteid kasutada erinevates rakendustes, sõltuvalt vajalikust täpsusest, võimsustaluvusest ja keskkonnatingimustest.
Kondensaator:

- Sümbol:

- Kirjeldus: Kondensaator salvestab elektrienergiat elektriväljas ja seda kasutatakse ajutiseks energia salvestamiseks, signaalide filtreerimiseks ja palju muuks.
- Tähis: C
- Ühik: Farad
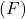
Elektriline mahtuvus on füüsikaline suurus, mis näitab, kui palju elektrilaengut suudab kondensaator hoida antud pinge juures. Elektrilise mahtuvuse ühik on farad ![]() .
.
Elektriline mahtuvus valemina:
Mahtuvus ( C ) määratakse järgmise valemiga:
![]()
Kus:
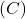 on mahtuvus
on mahtuvus 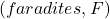 ,
,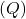 on elektrilaeng
on elektrilaeng 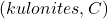 ,
,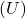 on pinge
on pinge 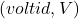 .
.
Mahtuvus paralleelplaatkondensaatori puhul:
Kui kondensaator koosneb kahest paralleelsest plaadist, siis mahtuvust ![]() saab arvutada järgmise valemi abil:
saab arvutada järgmise valemi abil:
![]()
Kus:
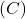 on kondensaatori mahtuvus
on kondensaatori mahtuvus 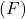 ,
,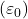 on vaakumi dielektriline läbitavus
on vaakumi dielektriline läbitavus 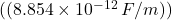 ,
,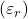 on materjali suhteline dielektriline läbitavus,
on materjali suhteline dielektriline läbitavus,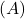 on plaadi pindala
on plaadi pindala 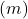 ,
,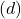 on plaatide vaheline kaugus
on plaatide vaheline kaugus 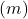 .
.
Energia kondensaatoris
Kondensaatoris salvestatud energia ( E ) on seotud mahtuvuse ja pinge vahel järgmise valemiga:
![]()
Kus:
- ( E ) on energia (džaulides, J),
- ( C ) on mahtuvus (F),
- ( U ) on pinge (V).
Ajast sõltuv pinge tühjeneval kondensaatoril:
Kui kondensaator tühjeneb läbi takisti ( R ), muutub pinge ajas vastavalt järgmisele eksponentsiaalsele valemile:
![]()
Kus:
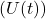 on pinge kondensaatoril ajahetkel
on pinge kondensaatoril ajahetkel 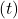 ,
,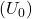 on algne pinge,
on algne pinge,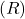 on takistus
on takistus 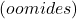 ,
,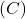 on mahtuvus
on mahtuvus 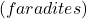 ,
,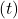 on aeg
on aeg 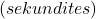 .
.
Need on peamised valemid, mis käsitlevad elektrilist mahtuvust ja kondensaatorite käitumist vooluringis.
Kondensaatorite tööpõhimõte ja liigitus on sügavamalt vaadeldes seotud nende füüsikaliste omaduste ja elektrotehniliste funktsioonidega, mida kasutatakse laialdaselt nii analoog- kui ka digitaalelektroonikas. Alljärgnevalt selgitan põhjalikumalt kondensaatori tööpõhimõtet, põhifunktsioone ja erinevate tüüpide detaile.
Kondensaatori töö sõltub sellest, kas see on ühendatud alalisvoolu (DC) või vahelduvvoolu (AC) ahelaga. Siin on ülevaade, kuidas kondensaator erinevates vooluahelates käitub.
Kondensaatori töö alalisvoolu (DC) ahelas
Alalisvoolu ![]() puhul kondensaator kogub ja salvestab elektrilaengut, kuid kui see on täis laetud, hakkab see käituma kui avatud ahel.
puhul kondensaator kogub ja salvestab elektrilaengut, kuid kui see on täis laetud, hakkab see käituma kui avatud ahel.
- Laadimisfaas:
Kui kondensaator ühendatakse alalisvooluallikaga, hakkab see algselt laadima. Laeng koguneb kondensaatori plaatidele, tekitades neile vastaslaengud. Laadimisprotsessi jooksul voolab ahelas vool, kuid see väheneb, kui kondensaator täitub. Laadimisprotsessi kirjeldab järgmine valem:![Rendered by QuickLaTeX.com \[Q(t) = C U (1 - e^{-\frac{t}{RC}})\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-8f83f62f15345ab78ba075ea04a47ff0_l3.png)
Kus:
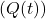 on laeng ajahetkel
on laeng ajahetkel 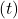 ,
,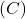 on mahtuvus,
on mahtuvus,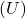 on pinge,
on pinge,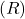 on takistus,
on takistus,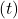 on aeg.
on aeg.
- Püsifaas (laetud kondensaator):
Kui kondensaator on täielikult laetud, voolutugevus ahelas langeb nullini ja kondensaator säilitab kogutud laengu. Seejärel hakkab see käituma kui avatud lüliti, mis blokeerib alalisvoolu edasise liikumise. - Tühjenemisfaas:
Kui alalisvooluallikas eemaldada ja kondensaator ühendada takistiga, hakkab see tühjenema. Tühjenemise käigus voolab vool, kuid see väheneb aja jooksul ja lõpuks kondensaator kaotab kogu oma laengu. Tühjenemise ajal langeb pinge eksponentsiaalselt:![Rendered by QuickLaTeX.com \[U(t) = U_0 e^{-\frac{t}{RC}}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-8c0e4f6759be6fa4ab373a8389ac3357_l3.png)
Kus:
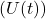 on pinge ajahetkel
on pinge ajahetkel 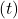 ,
,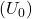 on algne pinge,
on algne pinge,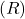 on takistus,
on takistus,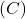 on mahtuvus.
on mahtuvus.
Kokkuvõte DC ahelas:
- Alalisvoolu (DC) ahelas käitub kondensaator esmalt voolujuhtmena, kuni see on laetud, ja seejärel toimib kui avatud ahel, mis ei luba voolu liikuda.
Kondensaatori töö vahelduvvoolu (AC) ahelas
Vahelduvvoolu (AC) ahelas kondensaator pidevalt laeb ja tühjeneb, kuna vahelduvvoolu pinge muutub pidevalt suuna ja suuruse poolest. See võimaldab kondensaatoril pidevalt voolu juhtida.
- Laadimine ja tühjenemine:
Vahelduvvoolu korral muutub pinge suund regulaarselt. Seetõttu kondensaator vaheldumisi laeb ja tühjeneb iga poolperioodi jooksul. Kui pinge suureneb ühes suunas, kondensaator laeb, ja kui pinge suund muutub, hakkab see tühjenema ja laadima vastupidises suunas. - Voolu juhtimine:
Kuna kondensaator pidevalt laeb ja tühjeneb, tekib ahelas faasinihe pinge ja voolu vahel. Vool juhitakse ja see on 90 kraadi ees pinge faasist. See tähendab, et maksimaalne vool tekib siis, kui pinge muutub kõige kiiremini (läbib nullpunkti), ja maksimaalne pinge tekib siis, kui vool on null.
- Vool kondensaatoris vahelduvvoolu puhul on antud valemiga:
![Rendered by QuickLaTeX.com \[I(t) = C \frac{dU(t)}{dt}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-931a030088f706f9dbbe4eed60790207_l3.png)
Kus: 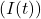 on vool,
on vool,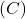 on mahtuvus,
on mahtuvus,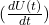 on pinge muutuse kiirus aja suhtes.
on pinge muutuse kiirus aja suhtes.
- Takistus ehk reaktants:
Vahelduvvoolu puhul pakub kondensaator takistust, mida nimetatakse kapatsiitvseks reaktantsiks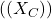 . Reaktants sõltub vahelduvvoolu sagedusest:
. Reaktants sõltub vahelduvvoolu sagedusest:![Rendered by QuickLaTeX.com \[X_C = \frac{1}{2 \pi f C}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-ae571e033f242301829ebf9cd1b49290_l3.png)
Kus:
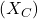 on kapatsiitvne reaktants
on kapatsiitvne reaktants 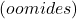 ,
,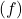 on vahelduvvoolu sagedus
on vahelduvvoolu sagedus 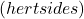 ,
,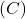 on mahtuvus
on mahtuvus 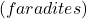 . Mida kõrgem on sagedus, seda väiksem on takistus, ja vastupidi.
. Mida kõrgem on sagedus, seda väiksem on takistus, ja vastupidi.
Kokkuvõte AC ahelas:
- Vahelduvvoolu (AC) ahelas juhib kondensaator voolu pidevalt, kuna see laeb ja tühjeneb pidevalt vastavalt pingemuutustele. Kondensaator loob voolu ja pinge vahele faasinihke, kus vool on ees pinge faasist.
Kondensaatorite võrdlus DC ja AC ahelas:
- DC ahelas toimib kondensaator ajutiselt kui juht, kuni see on laetud, ja seejärel muutub see avatud ahelaks.
- AC ahelas töötab kondensaator pidevalt, juhtides vahelduvvoolu läbi, laades ja tühjenedes vastavalt vahelduvvoolu muutustele.
Seega on kondensaatori roll DC ahelas laengu salvestamine ja AC ahelas energia ajutine salvestamine ja voolu juhtimine faasinihte tekitamise kaudu.
Kondensaatori tööpõhimõte
Kondensaator koosneb kahest paralleelsest juhtivast plaadist (elektroodid), mis on eraldatud mittejuhtiva materjaliga ehk dielektrikuga. Kui nendele plaatidele rakendatakse pinget, hakkavad elektronid liikuma ühelt plaadilt teisele: üks plaat saab liigse negatiivse laengu (elektronid), samal ajal kui teine plaat kaotab sama palju elektrone ja omandab positiivse laengu. See tekitab elektrivälja plaatide vahele.
Kondensaatori põhifunktsioon on elektrienergia ajutine salvestamine elektrivälja kujul, mida saab hiljem vabastada. Mahtuvus (C) määrab, kui palju elektrilaengut kondensaator võib salvestada, ning seda mõõdetakse faradites (F). Mahtuvust määravad:
- Plaatide pindala – suurem pindala suurendab mahtuvust.
- Plaadi vaheline kaugus – väiksem kaugus suurendab mahtuvust.
- Dielektriku omadused – erinevad materjalid võimaldavad paremat või halvemat laengu salvestamist.
Kui kondensaator on ühendatud vooluringi, suudab ta energiat salvestada ja vabastada väga kiiresti, mis muudab selle oluliseks komponendiks nii vahelduv- kui ka alalisvooluringides, eriti silumiseks, filtrite ehitamiseks ja energiasalvestuseks.
Kondensaatori liigitus
Kondensaatorid jagunevad mitmeks erinevaks tüübiks, sõltuvalt nende ehitusest, materjalist, mahtuvusest ja kasutusvaldkonnast.
1. Elektrolüütkondensaatorid
Elektrolüütkondensaatorid kasutavad elektrolüüdi lahust dielektrikuna, mis võimaldab saavutada suurema mahtuvuse väikese füüsilise suurusega. Nende suur mahtuvus teeb nad sobivaks kasutamiseks toiteallikates, kus on vaja suurt energiasalvestusvõimet ja pingekõikumiste silumist. Samas on need polaarised, mis tähendab, et need tuleb ühendada õige polaarsusega (positiivne klemm plussile ja negatiivne miinusele). Vale ühendamine võib põhjustada kondensaatori plahvatuse või lekke.
- Alumiinium-elektrolüütkondensaator: Levinud ja odav. Kasutatakse sageli toiteallikates.
- Tantaal-elektrolüütkondensaator: Kompaktsem ja stabiilsem kui alumiiniumversioon, kuid tundlikum valele polaarsusele.
Tüüpiline mahtuvus: Mikrofaradid (µF) kuni millifaradid (mF).
2. Keraamilised kondensaatorid
Keraamilised kondensaatorid kasutavad dielektrikuna keraamilist materjali. Need on väikese mahtuvusega, kuid väga stabiilsed ja töökindlad. Keraamilisi kondensaatoreid kasutatakse peamiselt kõrgsagedusrakendustes ja võrgufiltrites, kus on oluline kõrge töökindlus ja kiire reageerimisaeg.
- MLCC (Multilayer Ceramic Capacitor): Kõrge mahtuvusega keraamilised kondensaatorid, mis koosnevad mitmest keraamilisest kihist, pakkudes paremat mahtuvuse-tiheduse suhet.
- Madalsageduskondensaatorid: Sobivad madalate sageduste jaoks ja väiksema pingetaluvusega.
Tüüpiline mahtuvus: Piko- kuni nanofaradid (pF kuni nF).
3. Plastkilekondensaatorid
Plastkilekondensaatorid kasutavad dielektrikuna õhukest plastkile, näiteks polüestrit või polüpropüleeni. Neid kasutatakse tavaliselt rakendustes, kus on vaja väga täpseid ja stabiilseid komponente, näiteks sagedusfiltrites ja mõõteahelates. Neid iseloomustab madal lekkevool ja pinge taluvus.
- Polüesterkile kondensaator: Kompaktne ja odav, laialdaselt kasutatav.
- Polüpropüleen-kile kondensaator: Suure täpsusega, kasutatakse täppisrakendustes.
Tüüpiline mahtuvus: Nanofaradid (nF) kuni mikrofaradid (µF).
4. Mika- ja klaaskondensaatorid
Need kondensaatorid kasutavad dielektrikuna mikat või klaasi. Need on tuntud oma erakordse stabiilsuse ja väga madala lekkevoolu poolest, mistõttu sobivad nad täppisrakendustesse, kus on oluline säilitada konstantne mahtuvus ka kõrgetel sagedustel ja temperatuuridel.
- Mika-kondensaator: Väga täpne ja madala hajumisega.
- Klaaskondensaator: Töötab hästi kõrgetel pingetel ja on äärmiselt vastupidav.
Tüüpiline mahtuvus: Piko- kuni nanofaradid (pF kuni nF).
- Muskoviit (valge mika):
Kõige levinum mikatüüp, mida kasutatakse elektriisolatsioonis ja elektroonikaseadmetes.- Biotiit (must mika):
Sisaldab rohkem rauda ja on seetõttu vähem kasutatud elektrilises isolatsioonis, kuid seda kasutatakse mõnedes tööstuslikes rakendustes.
MIKA
MIKA võib olenevalt kontekstist tähendada erinevaid asju, kuid elektroonikas ja materjaliteaduses viitab mika tavaliselt läbipaistvale mineraalile, mida kasutatakse elektriisolatsiooniks. Mika on mineraalide rühm, mis koosneb peamiselt alumiiniumist ja kaaliumist ning mida iseloomustab hea mehaaniline tugevus, painduvus ja soojusisolatsioon.
Mika kasutusalad elektroonikas ja tehnoloogias:
- Isolatsioonimaterjal:
Mika talub väga hästi kõrgeid temperatuure ja sellel on suurepärased elektrilised isolatsiooniomadused. Seetõttu kasutatakse seda elektri- ja elektroonikaseadmetes, nagu:
- Kondensaatorid (kondekakondensaatorid),
- Elektrilised kütteseadmed ja isolatsiooniplaadid,
- Transistoride ja pooljuhtide soojusjuhtides.
- Mikakondensaatorid:
Kondensaatorid, kus isolatsioonimaterjalina kasutatakse mika, tuntud kui mikakondensaatorid, on hinnatud nende täpsuse, stabiilsuse ja töökindluse tõttu. Neid kasutatakse kohtades, kus on vajalik püsiv ja usaldusväärne töö ka ekstreemsetes tingimustes. - Soojusjuhtimine:
Mika lehtedel on hea soojusjuhtivus, seetõttu kasutatakse seda komponentide ja jahutusradiaatorite vahel, et aidata soojust hajutada ja samal ajal tagada elektriline isolatsioon.
Mika omadused:
- Suur soojus- ja elektritakistus: Mika on suurepärane soojusisolatsioonimaterjal ja talub väga kõrgeid temperatuure (kuni 1000 °C).
- Paindlikkus ja läbipaistvus: Mika lehed on õhukesed ja painduvad ning neid saab lõigata väga õhukesteks kihtideks.
- Keemiline stabiilsus: Mika on vastupidav keemilistele reaktsioonidele ja ei reageeri kergesti teiste materjalidega, mistõttu sobib see hästi ekstreemsetesse keskkondadesse.
Mika tüübid:
- Muskoviit (valge mika):
Kõige levinum mikatüüp, mida kasutatakse elektriisolatsioonis ja elektroonikaseadmetes. - Biotiit (must mika):
Sisaldab rohkem rauda ja on seetõttu vähem kasutatud elektrilises isolatsioonis, kuid seda kasutatakse mõnedes tööstuslikes rakendustes.
Kokkuvõte:
Mika on mineraal, mida hinnatakse selle suurepäraste elektriliste ja soojusisolatsiooniomaduste tõttu. Elektroonikas ja elektrotehnikas kasutatakse seda peamiselt elektriisolatsioonina ning kuumuse ja kulumise suhtes vastupidavate komponentidena.
5. Superkondensaatorid
Superkondensaatorid on unikaalsed oma äärmiselt suure mahtuvuse poolest. Need on võimelised salvestama suurt hulka energiat ja on hübriid kondensaatorite ja patareide vahel. Neid kasutatakse näiteks kiirlaadimissüsteemides ja energia salvestamiseks lühiajalistes rakendustes. Superkondensaatorid suudavad pakkuda kiiret energiapuhangut, kuid ei suuda seda pikaajaliselt hoida nagu patareid.
- Tüüpiline mahtuvus: Kilo- kuni tuhanded faradid (kF kuni F).
Superkondensaator
Superkondensaator: Tööpõhimõte ja kasutus
Mis on superkondensaator?
Superkondensaator ehk ultrakondensaator on elektrooniline komponent, mis suudab salvestada palju suuremat kogust energiat kui tavalised kondensaatorid, kuid ei ole otseselt võimeline asendama akusid pikaajalises energiavarustuses. Superkondensaatorid ühendavad endas tavapärase kondensaatori kiire laadimise ja tühjenemise omadused koos suurema energiasalvestusvõimega, mis viib need aku ja kondensaatori vahepealsesse klassi.
Superkondensaatori mahtuvus on väga suur, tavaliselt mõõdetakse seda faradites (F), võrreldes tavaliste kondensaatorite mikro- ja nanofaraditega.
Superkondensaatori tööpõhimõte
Superkondensaator töötab, salvestades energiat elektrostaatilise ja elektrokeemilise protsessi kaudu. Erinevalt elektrolüütkondensaatorist, kus energia salvestatakse ainult elektrivälja kaudu, kasutavad superkondensaatorid ära kahe mehhanismi kombinatsiooni:
- Elektrostaatiline mahtuvus: See on sama põhimõte, mida kasutatakse tavalistes kondensaatorites, kus laeng koguneb kahe elektroodi vahel, mis on eraldatud dielektrikuga. Superkondensaatoris on elektroodide pind väga suur ja nende vaheline kaugus väga väike.
- Pseudomahtuvus: Tekib elektrokeemiliste reaktsioonide kaudu elektroodidel, mis suurendavad oluliselt energiatihedust, võrreldes tavalise kondensaatoriga. See protsess kasutab ära ioonide neeldumise ja desorptsiooni elektroodi pinnal, mille kaudu toimub täiendav energiasalvestus.
Superkondensaator koosneb kahest elektroodist (sageli valmistatud aktiivsöest või muudest süsinikmaterjalidest), mida eraldab elektrolüüt. Kui neile elektroodidele rakendatakse pinget, kogunevad ioonid elektroodide pinnale, tekitades suure laengu ja elektrivälja. Kuna ioonide liikumine ja neeldumine elektroodi pinnale on väga kiire, saab superkondensaator kiiresti laadida ja tühjeneda.
Superkondensaatorite töö ja omaduste kirjeldamiseks kasutatakse mitmeid valemeid, mis on seotud nende mahtuvuse, energia ja laenguga. Allpool on mõned olulisemad valemid, mis selgitavad superkondensaatorite toimimist ja omadusi.
Mahtuvus (C)
Mahtuvus on superkondensaatori võime salvestada laengut ja seda mõõdetakse faradites (F).
![]()
- C – mahtuvus (faradites, F)
- Q – laeng (kulonites, C)
- V – pinge (voltides, V)
See valem näitab, et mahtuvus on otseselt seotud laengu hulga ja pingega. Mida suurem on mahtuvus, seda rohkem laengut suudab superkondensaator madala pinge juures salvestada.
Energia salvestamine (E)
Superkondensaatoris salvestatud energia arvutatakse järgmise valemi abil:
![]()
- E – energia (džaulides, J)
- C – mahtuvus (faradites, F)
- V – pinge (voltides, V)
See valem näitab, et salvestatud energia sõltub mahtuvusest ja pinge ruudust. Kuna energia kasvab koos pinge ruuduga, on kõrgema tööpingega superkondensaatoritel suurem energiatihedus.
Laengu ja tühjenemise aeg
Superkondensaatori laengu ja tühjenemise aega saab kirjeldada vastupanu ja mahtuvuse korrutisega:
![]()
- τ – ajakonstant (sekundites, s)
- R – takistus (oomides, Ω)
- C – mahtuvus (faradites, F)
Ajakonstant näitab, kui kiiresti superkondensaator suudab täis laadida või tühjeneda läbi antud takistuse. Tüüpiliselt loetakse kondensaatorit tühjaks pärast 5τ, mille jooksul on superkondensaator kaotanud umbes 99% oma salvestatud energiast.
Maksimaalne vool (I)
Superkondensaator suudab pakkuda suurt voolu, kuid selle voolu piiramiseks kasutatakse järgmisi valemeid:
![]()
- I – vool (amprites, A)
- V – pinge (voltides, V)
- R – takistus (oomides, Ω)
See on Ohmi seadus, mis näitab, et vool superkondensaatoris sõltub pingest ja takistusest.
Materjalid, mida kasutatakse superkondensaatorite tootmisel
Superkondensaatorid koosnevad mitmetest erinevatest materjalidest, mis mõjutavad nende omadusi, sealhulgas mahtuvust, vastupidavust ja energiatihedust.
1. Elektroodid
- Aktiivsüsi (carbon-based materials): Aktiivsüsi on kõige sagedamini kasutatav materjal superkondensaatorites elektroodide valmistamiseks. Selle eelis on suur pindala ja head juhtivusomadused, mis võimaldavad tal salvestada suuri koguseid elektrilaengut.
- Grafiit ja grafeen: Neid kasutatakse, et suurendada elektroodide juhtivust ja vähendada sisetakistust, pakkudes paremaid tulemusi võrreldes aktiivsöega.
- Metalloksiidid: Näiteks ruteeniumoksiid (RuO₂) ja mangaanoksiid (MnO₂) kasutatakse pseudomahtuvus-superkondensaatorites. Need materjalid aitavad suurendada superkondensaatori mahtuvust, kuna nad suudavad talletada laengut läbi elektrokeemiliste reaktsioonide.
- Juhtivad polümeerid: Polümeerid, nagu polüaniliin (PANI) ja polüpürrool (PPY), kasutatakse samuti elektroodideks, kuna need pakuvad kõrget juhtivust ja head elektrokeemilist stabiilsust.
2. Elektrolüüdid
- Vees lahustuvad elektrolüüdid: Sageli kasutatakse vesi-elektrolüüte (nt kaaliumhüdroksiid KOH või väävelhape H₂SO₄) madala pingega superkondensaatorites. Need elektrolüüdid on madala resistentsusega ja võimaldavad kiiret laengu üleandmist elektroodide ja elektrolüüdi vahel.
- Orgaanilised elektrolüüdid: Orgaanilised lahustid (nt atsetonitriil või propüleenkarbonaat) on kasutusel kõrgema pingega superkondensaatorites (tavaliselt kuni 2,7–3 V), kuna need taluvad kõrgemaid pingeid ja vähendavad elektrolüüdi lagunemist.
- Ioonvedelikud: Need on ioonide segu, millel on väga madal aururõhk ja hea soojusjuhtivus, mis võimaldab neil töötada laias temperatuurivahemikus ja kõrgetel pingetel.
3. Separaatormaterjalid
- Polümeerid: Polümeeride, nagu polüpropüleen (PP) ja polüetüleen (PE), kasutamine superkondensaatorite separaatormaterjalides tagab ioonide liikumise elektroodide vahel, hoides samal ajal elektroode füüsiliselt lahus, et vältida lühiseid.
- Tselluloos: Mõnel juhul kasutatakse ka tselluloosmaterjale, mis on biolagunevad ja odavamad alternatiivid.
Superkondensaatori eelised ja tulevikusuunad materjalides
- Grafeen on uurimuses väga paljutõotav materjal, kuna selle erakordselt suur pindala ja juhtivus võivad oluliselt suurendada superkondensaatorite mahtuvust ja võimsustihedust.
- Nanomaterjalid: Erinevad nanomaterjalid, näiteks süsiniknanotorud ja nanokomposiidid, võivad pakkuda uusi võimalusi energiasalvestuseks, muutes superkondensaatorid veelgi tõhusamaks ja võimsamaks.
Superkondensaatorite arengus mängivad olulist rolli materjalid, mis suudavad pakkuda kõrgemat energiatihedust ja paremat jõudlust. Uued uurimissuunad keskenduvad energiasalvestusmaterjalidele, mis suudavad ületada praegusi piiranguid ja laiendada superkondensaatorite kasutusvõimalusi.
Superkondensaatorite peamised omadused:
- Väga suur mahtuvus: Superkondensaatorid võivad ulatuda mahtuvusteni tuhandetes faradites (F), võrreldes tavakondensaatorite mikrofaradite (µF) või millifaraditega (mF).
- Kiire laadimine ja tühjenemine: Superkondensaatorid suudavad laadida ja tühjeneda sekundite jooksul, samas kui akud võtavad laadimiseks aega tunde.
- Pikk elutsükkel: Superkondensaatorid taluvad palju rohkem laadimis-tühjenemistsükleid (sadu tuhandeid või isegi miljoneid) võrreldes akudega, millel on piiratud tsüklite arv.
- Suur võimsustihedus: Superkondensaatorid suudavad pakkuda ja neelata suurt voolu väga kiiresti, mis teeb need sobivaks rakendusteks, kus on vaja kiiret energiapuhangut.
- Madal energiatihedus: Võrreldes akudega on superkondensaatorite energiatihedus väiksem, mistõttu ei sobi need pikaajaliseks energia salvestamiseks.
Superkondensaatori liigitus
Superkondensaatorid jaotatakse tavaliselt kaheks põhikategooriaks sõltuvalt nende töömehhanismist ja materjalidest:
- Kahekihilised kondensaatorid (EDLC – Electric Double-Layer Capacitors):
- Need kasutavad energia salvestamiseks ainult elektrostaatilist laengut, kus laengud kogunevad kahe elektroodi vahele. Neid iseloomustab suur võimsustihedus, kuid suhteliselt madal energiatihedus.
- Näited: Aktiivsüsi-elektroodidega superkondensaatorid.
- Pseudomahtuvuskondensaatorid:
- Need kasutavad energia salvestamiseks elektrokeemilisi reaktsioone (sarnaselt akudele), mis suurendab energiatihedust võrreldes kahekihiliste kondensaatoritega. Nende laadimisprotsess põhineb ioonide neeldumisel ja desorptsioonil elektroodi pinnale.
- Näited: Metalloksiid-elektroodidega või polümeerelektroodidega superkondensaatorid.
Superkondensaatori kasutusvaldkonnad
Superkondensaatorid on leidnud laialdast kasutust paljudes valdkondades, kus on vaja kiiret energiaedastust või kus kasutatakse tsüklilist laadimis- ja tühjenemisprotsessi.
- Automotive ja transport:
- Superkondensaatorid kasutatakse elektrisõidukites pidurdamisel energia rekupeerimiseks ja selle kiireks vabastamiseks kiirendamisel. Samuti on nad kasutusel hübriidautodes koos akudega, kus nad täiendavad akusid, pakkudes kiiret energiapuhangut.
- Energia salvestamine ja taastuvenergia:
- Superkondensaatorid sobivad energiasalvestuseks tuule- ja päikeseenergia süsteemides, kus nad suudavad kiiresti salvestada ja vabastada energiat elektrivõrgu tasakaalustamiseks.
- Võrgutoite varundamine:
- Superkondensaatorid pakuvad lühiajalist varutoidet, näiteks UPS-süsteemides (katkematu voolu allikas), kus nad suudavad hoida seadmed töös lühikese voolukatkestuse ajal või kuni põhitoiteallikas taastatakse.
- Elektroonika:
- Superkondensaatorid kasutatakse väikese võimsusega seadmetes, näiteks kellade ja mälumoodulite varutoiteks, kus on oluline tagada stabiilne toiteallikas lühiajaliselt, eriti voolukatkestuste ajal.
- Tööstus ja telekommunikatsioon:
- Superkondensaatorid suudavad pakkuda lühiajalist energiat mitmesugustes telekommunikatsioonisüsteemides, andes seadmetele toidet lühikeste katkestuste või voolu kõikumiste ajal.
Superkondensaatori eelised ja piirangud
Eelised:
- Väga kiire laadimis- ja tühjenemiskiirus.
- Pikk elutsükkel ja talub palju laadimis-tühjenemistsükleid.
- Suur võimsustihedus, mis võimaldab pakkuda suurt voolu lühikese aja jooksul.
- Keskkonnasõbralikumad kui akud, kuna ei sisalda mürgiseid kemikaale.
Piirangud:
- Madalam energiatihedus kui akudel, mis tähendab, et need ei sobi pikaajalise energia salvestamiseks.
- Võib vajada erilahendusi kõrgete pingete rakendustes, kuna nende tööpinge on madalam kui tavapärastel akudel.
Kokkuvõttes on superkondensaatorid ideaalne lahendus olukordades, kus on vaja kiiret energiavoogu ja pikka elutsüklit, kuid nad ei sobi pikaajalisteks energiavarustuse lahendusteks nagu akud.
Kondensaatorite põhifunktsioonid
- Voolu silumine ja pingekõikumiste tasandamine: Kondensaatorid aitavad siluda voolu ja pingeid, eriti toiteallikates, et eemaldada soovimatud kõikumised.
- Filtreerimine: Kõrgsagedusfiltrites kasutatakse kondensaatoreid, et eemaldada müra ja soovimatud sagedused elektrisignaalist.
- Ajastamine ja signaalide muutmine: Ajastusahelates, nagu multivibraatorid ja ostsillaatorid, määravad kondensaatorid ajaintervallid ja sagedused.
- Energia salvestamine: Kondensaatorid salvestavad ajutiselt energiat, mida saab vabastada kiireks energiapuhanguks või järk-järgult.
Kokkuvõttes sõltub kondensaatori tüüp ja kasutusviis suuresti rakenduse nõuetest, näiteks mahtuvus, pinge taluvus, stabiilsus ja füüsilised mõõtmed. Kondensaatorid on asendamatud komponendid mitmesugustes elektroonikaseadmetes, alates lihtsatest toiteallikatest kuni keeruliste andmetöötlussüsteemideni.
Induktiivpool (Mähis)

- Sümbol:

- Kirjeldus: Induktiivpool salvestab energiat magnetväljas ja seda kasutatakse sagedusfiltrites, energia salvestamisel ja mujal.
- Tähis: L
- Ühik: Henry (H)
Induktiivsus on füüsikaline suurus, mis iseloomustab induktiivpooli (mähise) võimet tekitada elektromotoorjõudu (pinget) voolu muutumise korral. Induktiivsuse ühik on henri (H).
Induktiivsus sirge mähise jaoks:
Induktiivsuse ![]() saab sirge mähise jaoks arvutada järgmise valemi abil:
saab sirge mähise jaoks arvutada järgmise valemi abil:
![]()
Kus:
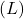 on induktiivsus
on induktiivsus 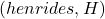 ,
,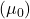 on vaakumi magnetiline läbitavus
on vaakumi magnetiline läbitavus 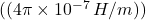 ,
,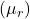 on mähise südamiku suhteline magnetiline läbitavus (dielektrilise materjali omadus),
on mähise südamiku suhteline magnetiline läbitavus (dielektrilise materjali omadus),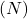 on mähise keerude arv,
on mähise keerude arv,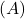 on mähise ristlõike pindala
on mähise ristlõike pindala 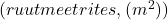 ,
,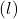 on mähise pikkus
on mähise pikkus 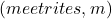 .
.
2. Elektromagnetiline induktsioon (Faraday seadus):
Kui voolu muutumine ajas tekitab mähises pinge, siis selle pinge ( \varepsilon ) on antud valemiga:
![]()
Kus:
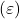 on induktiivpooli tekitatud pinge
on induktiivpooli tekitatud pinge 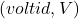 ,
,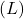 on induktiivsus
on induktiivsus 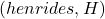 ,
,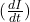 on voolu muutumise kiirus ajas
on voolu muutumise kiirus ajas 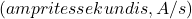 .
.
3. Induktiivne reaktants vahelduvvoolu puhul:
Vahelduvvoolu (AC) puhul takistab induktiivpool voolu, mis tekib selle magnetväljas, ja see takistus on tuntud kui induktiivne reaktants ( X_L ):
![]()
Kus:
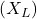 on induktiivne reaktants
on induktiivne reaktants 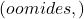 ,
,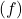 on vahelduvvoolu sagedus
on vahelduvvoolu sagedus 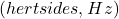 ,
,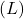 on induktiivsus
on induktiivsus 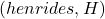 .
.
Mida suurem on sagedus või induktiivsus, seda suurem on induktiivne reaktants, mis piirab voolu läbimist mähisest.
4. Energia induktiivpoolis:
Induktiivpooli magnetvälja salvestatud energia ( E ) on antud valemiga:
![]()
Kus:
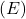 on energia
on energia 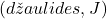 ,
,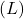 on induktiivsus
on induktiivsus 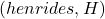 ,
,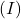 on vool
on vool 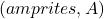 .
.
5. Induktiivpooli faasinihe vahelduvvoolu puhul:
Vahelduvvoolu (AC) korral tekitab induktiivpool voolu ja pinge vahele faasinihke, kus pinge on voolu faasist 90 kraadi ees. See tähendab, et maksimaalne pinge saavutatakse siis, kui vool hakkab muutuma.
Need on peamised valemid, mis käsitlevad induktiivsust ja induktiivpoolide käitumist vooluahelates.
Induktiivpooli (Mähise) tööpõhimõte ja liigitus
Tööpõhimõte
Induktiivpool, mida sageli nimetatakse ka mähiseks, on elektrotehniline komponent, mille peamine funktsioon on salvestada energiat magnetvälja kujul, kui vool läbib seda. Mähis koosneb tavaliselt isoleeritud traadist, mis on keritud silindrikujuliselt või spiraalina ümber tuuma, mis võib olla õhu või ferromagnetilise materjaliga (nt raud). Induktiivpoolsuse (L) suurust mõõdetakse henrites (H).
Kui vool liigub läbi mähise, tekitab see selle ümber magnetvälja. Mähise elektritakistus on minimaalne, kuid selle induktiivtakistus takistab voolu muutusi ahelas. Mida kiirem on voolu muutus, seda suurem on vastutekkiv induktiivne pingelang. Seda nähtust nimetatakse induktsiooniks ja selle kaudu hoiab induktiivpool energia salvestamist magnetväljas.
Induktiivpooli põhiomadused:
- Induktiivsus (L) – määrab, kui tõhusalt mähis salvestab energiat magnetvälja kujul. See sõltub mähise traadi keerdude arvust, keerdude tihedusest, südamiku materjalist ja südamiku geomeetriast.
- Eneseinduktsioon – kui voolu muutus mähises tekitab selles endas pinge, mis püüab vastu seista voolu muutusele.
- Mutuaalne induktsioon – esineb kahe või enama mähise vahel, kus ühe mähise magnetväli indutseerib teises mähises pinge (nt trafo tööpõhimõte).
Induktiivpooli liigitus
Mähised liigitatakse mitmel viisil, sõltuvalt nende konstruktsioonist, funktsioonist ja kasutusvaldkonnast.
1. Õhusüdamikuga mähised
Need on mähised, millel ei ole magnetilist südamikku – traadi keerdude vahel on lihtsalt õhk või muu mitte-magnetiline aine. Sellised mähised on lihtsad ja töökindlad, kuid nende induktiivsus on madal. Neid kasutatakse sageli raadio- ja kõrgsagedusrakendustes, kus on oluline vältida südamiku kaod.
- Tunnused: Madal induktiivsus, sobib kõrgetele sagedustele.
- Tüüpiline kasutus: Raadiovastuvõtjad, antennide mähised.
2. Raudsüdamikuga mähised
Selliste mähiste puhul on traadikeerdude sees ferromagnetiline südamik (näiteks raud või feriit), mis suurendab mähise induktiivsust, kuna südamik keskendab ja tugevdab magnetvälja. Raudsüdamikuga mähiseid kasutatakse peamiselt madalsagedusrakendustes ja kohtades, kus on vaja suurt induktiivsust.
- Tunnused: Suurem induktiivsus võrreldes õhusüdamikuga mähistega, kuid südamiku materjal võib tekitada kaotusi (nt hüstereesikaod ja pöörisvoolud).
- Tüüpiline kasutus: Võimsusmuundurid, trafod, elektromagnetid.
3. Ferriit- või pulbersüdamikuga mähised
Ferriit- ja pulbersüdamikuga mähised on spetsiaalselt loodud töötama kõrgetel sagedustel, pakkudes paremat jõudlust ja väiksemaid kaotusi võrreldes raudsüdamikuga mähistega. Ferriitmaterjal on mittejuhtiv ja suudab vältida pöörisvoolukadusid, mis esinevad kõrgsageduslikes rakendustes.
- Tunnused: Kõrgsageduste jaoks sobivad, väiksemad kaod ja suurem efektiivsus.
- Tüüpiline kasutus: Raadiosagedusmuundurid, filtrid, trafod.
4. Toroidmähised
Toroidmähised on spetsiaalse kujuga mähised, kus traat on keritud rõngakujulise (toroidse) südamiku ümber. Toroidmähised pakuvad paremat magnetvälja suunamist ja väiksemat kiirgust väljapoole mähist, vähendades elektromagnetilisi häireid (EMI).
- Tunnused: Kompaktne ja tõhus magnetvälja suunamine, väiksemad lekkeväljadel põhinevad kaod.
- Tüüpiline kasutus: Võimsustrafod, raadiosagedusfiltrid.
5. Võimsusinduktorid
Võimsusinduktorid on suure võimsustaluvusega mähised, mis on mõeldud töötama kõrge vooluga rakendustes, kus on vaja energiat salvestada ja seejärel kiiresti vabastada. Tavaliselt kasutatakse neid toiteahelates ja muundurites.
- Tunnused: Kõrge voolutaluvus, madal takistus.
- Tüüpiline kasutus: SMPS (Switch Mode Power Supplies), DC-DC muundurid.
Mähiste kasutusvaldkonnad ja funktsioonid
Mähiseid kasutatakse laialdaselt erinevates elektrotehnilistes rakendustes, alates energiasalvestusest kuni signaalide filtreerimiseni. Peamised funktsioonid ja kasutusvaldkonnad on järgmised:
1. Energia salvestamine
Mähis salvestab energiat magnetvälja kujul, kui vool läbib seda. Seda energiat saab hiljem vabastada, kui vool väheneb või suunatakse teise vooluahelasse. See omadus on eriti oluline võimsusahelates, näiteks lülitusmuundurites ja pingeregulaatorites.
Mähise energia salvestamise põhimõte põhineb sellel, et kui vool läbib mähist, siis tekib selle ümber magnetväli. Mähis suudab salvestada energiat selles magnetväljas seni, kuni vool läbib mähist. Kui vool hakkab vähenema või katkeb, siis see magnetväli hakkab kokku kukkuma ja mähisesse tekib pingelang, mis suunab energia tagasi vooluringi.
See omadus on eriti kasulik ja oluline võimsusahelates, näiteks:
- Lülitusmuundurites: Mähised aitavad muuta pinget efektiivselt. Kui muundatakse näiteks alalisvoolu madalast pingest kõrgeks või vastupidi, kasutatakse mähiseid energia ajutiseks salvestamiseks ja vabastamiseks.
- Pingeregulaatorites: Mähised aitavad stabiliseerida voolu ja pinget. Kui süsteemis on voolu- või pingekõikumisi, siis mähise kaudu on võimalik säilitada stabiilsus, kuna ta suudab ajutiselt energiat salvestada ja seejärel vajadusel vabastada, hoides süsteemi töö stabiilsena.
Kokkuvõttes toimib mähis energiapuhvrina, mis võimaldab ajutiselt talletada energiat magnetvälja kujul ning seejärel sujuvalt vabastada, kui seda vajatakse vooluringis, aidates seeläbi stabiliseerida ja juhtida vooluringi tööd.
2. Filtreerimine ja silumine
Mähised koos kondensaatoritega moodustavad LC-filtrid, mis filtreerivad välja soovimatud sagedused signaalist. Näiteks toiteallikates kasutatakse mähiseid pinge kõikumiste tasandamiseks ja müra vähendamiseks.
Filtreerimine ja silumine mähiste ja kondensaatorite abil toimib nii, et nad suudavad koos töötades kõrvaldada või vähendada soovimatuid sagedusi ja pinge kõikumisi elektrisüsteemis. See omadus on väga oluline, eriti toiteallikates ja elektroonikaseadmetes.
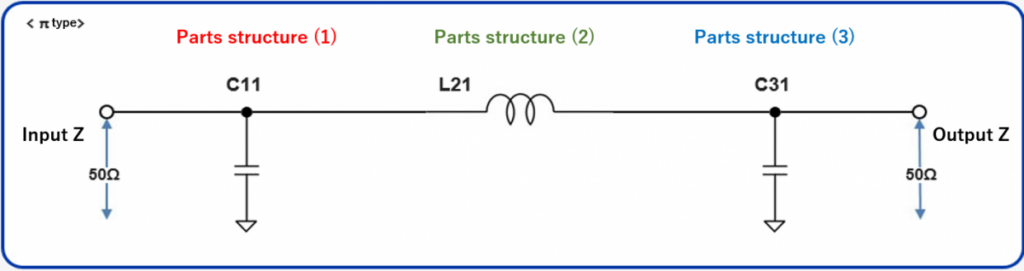
LC-filtrid
- LC-filtrid koosnevad mähisest (L) ja kondensaatorist (C). Need komponendid töötavad koos, et blokeerida teatud sagedused ja lasta teised läbi. LC-filtrid filtreerivad välja soovimatud kõrgsageduslikud häired või müra signaalist, säilitades samal ajal kasuliku signaali.
- Mähis (L) takistab kõrgsageduslike signaalide läbimist, samal ajal kui madalsageduslikud signaalid liiguvad mähisest vabalt läbi.
- Kondensaator (C) toimib vastupidi – see laseb kõrgsageduslikud signaalid läbi, aga blokeerib madalsageduslikud signaalid.
Kombineeritult suudavad LC-filtrid eemaldada soovimatud sagedused ja hoida vajalikud signaalid puhtad.
Pinge kõikumiste tasandamine ja müra vähendamine
- Toiteallikates on mähised kasutusel pinge ja voolu silumiseks ehk kõikumiste tasandamiseks. Elektrivõrgus või vooluallikas võib esineda müra või järske kõikumisi (nt lülitusmüra). Mähised aitavad neid kõikumisi sujuvamaks muuta, kuna nad salvestavad ja vabastavad energiat järk-järgult. See aitab vältida pinge järske muutusi ja hoida süsteemi stabiilsena. Näiteks toiteahelas aitavad mähised ja kondensaatorid koos vähendada kõrgsageduslikku müra, mis võib tekkida lülitusahelate tõttu, ning tagada stabiilse ja puhta pinge toidetavatele komponentidele.
LC-filtrid koosnevad induktiivpoolist (L) ja kondensaatorist (C) ning neid kasutatakse elektriliste signaalide filtreerimiseks teatud sageduste blokeerimiseks või lubamiseks. LC-filtrid on olulised elektroonikaseadmetes, nagu võimendid, raadiovastuvõtjad ja toiteallikad, kuna need suudavad puhastada signaale ja stabiliseerida süsteeme.
LC-filtrite peamised tüübid:
- Madalsagedusfilter (Low-pass filter):
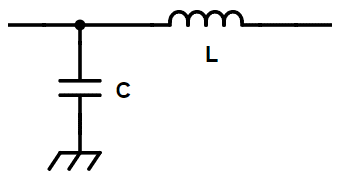
- Funktsioon: Laseb läbi madalad sagedused ja summutab kõrged sagedused.
- Kasutus: Kasutatakse sagedusvahemikus, kus madalsageduslik signaal peab läbima, kuid kõrgsageduslik müra tuleb blokeerida. Näiteks toiteallikates müra eemaldamiseks või helisüsteemides madalsageduslike komponentide edastamiseks.
- Ehitus: Tavaliselt koosneb induktiivpoolist ja kondensaatorist, kus induktiivpool on ühendatud signaaliteega ja kondensaator maaga, mis loob võime kõrgsagedusi summutada.
- Tüüpiline rakendus: Signaalide filtreerimine toiteahelates (nt vahelduvvoolu komponentide eemaldamine alalisvoolust), helisüsteemid, helivõimendid.
- Kõrgsagedusfilter (High-pass filter):
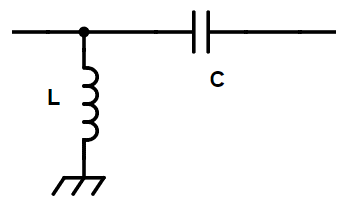
- Funktsioon: Laseb läbi kõrged sagedused ja summutab madalad sagedused.
- Kasutus: Kasutatakse rakendustes, kus on vaja edastada kõrgsageduslikke signaale ja blokeerida madalsageduslikud komponendid, näiteks helisüsteemides või raadiosageduslikes vastuvõtjates.
- Ehitus: Tavaliselt koosneb kondensaatorist ja induktiivpoolist, kus kondensaator on signaaliteel ja induktiivpool ühendatud maaga, mis summutab madalsagedusi.
- Tüüpiline rakendus: Kõrgsageduslike signaalide filtreerimine antennides, raadiosagedusfiltrid, helisüsteemides kõrgete sageduste edastamine.
- Ribapääsfilter (Band-pass filter):
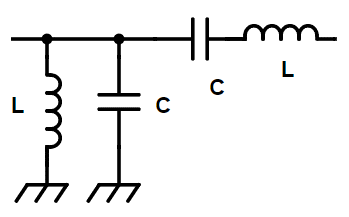
- Funktsioon: Laseb läbi ainult kindla sagedusriba ning summutab sagedused, mis jäävad sellest ribast kõrgemale või madalamale.
- Kasutus: Kasutatakse raadiosageduslikes rakendustes, kus soovitakse edastada ainult teatud sagedusala, näiteks raadiovastuvõtjates või traadita side süsteemides.
- Ehitus: Koosneb kahest LC komponendist (induktiivpool ja kondensaator), kus ühe kombinatsioon määrab filtri alumise piirsageduse ja teine kombinatsioon määrab ülemise piirsageduse.
- Tüüpiline rakendus: Raadio ja telekommunikatsiooniseadmed, sagedusmodulaatorid, võimendid.
- Ribakõrvalefilter (Band-stop filter):

- Funktsioon: Blokeerib kindla sagedusriba ja laseb läbi signaalid, mis on sellest ribast kas kõrgemal või madalamal.
- Kasutus: Kasutatakse süsteemides, kus on vaja summutada kindlaid sagedusi, näiteks häirivate sageduste või resonantsi eemaldamiseks.
- Ehitus: Tavaliselt sisaldab LC komponente nii, et nende kombinatsioon määrab kindla sagedusala, mis suletakse.
- Tüüpiline rakendus: Müra või ebasoovitavate sageduste eemaldamine raadio- ja sidevahendites, elektromagnetiliste häirete vähendamine.
LC-filtrite kasutusalad:
- Toiteallikad:
- Madalsagedusfiltrid kasutatakse alalisvoolu toiteallikates, et eemaldada vahelduvvoolu komponendid ja stabiliseerida alalisvoolu väljund.
- Raadiosageduslikud (RF) ahelad:
- Kõrgsagedusfiltrid ja ribapääsfiltrid leiavad kasutust raadiosageduslikes ahelates, näiteks raadiovastuvõtjates ja antennides, kus need aitavad kindla sagedusriba signaale edastada ja müra blokeerida.
- Helisüsteemid:
- Madalsagedusfiltrid ja kõrgsagedusfiltrid kasutatakse helisüsteemides, et filtreerida teatud sagedusvahemikud ja edastada ainult soovitud helikomponendid. Näiteks madalpääsfiltrid suunavad madalaid helisagedusi bassikõlaritesse ja kõrgpääsfiltrid suunavad kõrgsageduslikke helisid tweeter’itesse.
- Elektromagnetilise ühilduvuse (EMC) tagamine:
- Ribakõrvalefiltrid on olulised elektromagnetiliste häirete (EMI) eemaldamiseks, et vältida häireid teistest seadmetest või süsteemi enda sisemisi häireid.
LC-filtrid on väga olulised elektroonikas, kuna need võimaldavad soovitud signaalide edastamist ja soovimatute sageduste summutamist, mis tagab parema signaali kvaliteedi ja seadmete töökindluse.
Kokkuvõttes on filtreerimine ja silumine väga oluline funktsioon elektroonikaseadmetes, et hoida signaalid ja pinge võimalikult stabiilsena, eemaldades soovimatud sagedused ja vähendades müra.
3. Signaalide edastamine ja vastuvõtt
Raadiovastuvõtjates ja saatjates kasutatakse mähiseid sageduse selekteerimiseks ja võimendamiseks. Mähised aitavad luua resonantssagedusi, mis on vajalikud täpsete raadiosignaalide eristamiseks ja võimendamiseks.
Raadiovastuvõtjates ja saatjates mängivad mähised olulist rolli signaalide selekteerimisel ja võimendamisel. Need komponendid on vajalikud raadiosageduslike signaalide töötlemiseks ja täpsete sageduste eraldamiseks paljude teiste sageduste seast. Mähised töötavad tavaliselt koos kondensaatoritega, moodustades LC-ahelaid, mis võimaldavad resonantsi, et häälestuda soovitud sagedustele. Selgitame allpool põhjalikumalt, kuidas mähised töötavad ja milleks neid raadiovastuvõtjates ja saatjates kasutatakse.
Sageduse selekteerimine LC-resonantsahela abil
Raadiovastuvõtjates ja -saatjates on vaja valida täpne sagedus, et eraldada soovitud raadiosignaal paljude teiste signaalide ja mürade seast, mis levivad samaaegselt õhus. Selleks kasutatakse mähiseid koos kondensaatoritega LC-resonantsahelates.
Resonantsahel:
- LC-ahel koosneb mähisest (L) ja kondensaatorist (C), mis töötavad koos resonantsi loomiseks. Resonants tekib siis, kui induktiivpooli ja kondensaatori reaktiivtakistused tasakaalustavad teineteist, tekitades süsteemi jaoks spetsiifilise resonantssageduse ((f_r)).
Resonantssageduse valem on järgmine:
![]()
- L – mähise induktiivsus (henrites, H)
- C – kondensaatori mahtuvus (faradites, F)
- (f_r) – resonantssagedus (hertsides, Hz)
Selle valemi abil saab LC-ahel häälestuda kindlale sagedusele, kus mähise ja kondensaatori reaktiivtakistused üksteist tühistavad, võimaldades ainult selle sageduse läbimist. See tähendab, et ainult resonantssagedusega signaal pääseb edasi, samal ajal kui teised sagedused summutatakse. Sageduse selekteerimine on vajalik, et raadiovastuvõtja saaks tuvastada ja töödelda just seda konkreetset signaali, millele see on häälestatud (nt raadiojaam).
Näide:
Kui soovid kuulata 98 MHz raadiojaama, peab raadiovastuvõtja LC-ahel olema häälestatud resonantssagedusele 98 MHz. Ahel blokeerib kõik teised sagedused peale 98 MHz, võimaldades edastada vaid soovitud raadiosignaali.
Signaali võimendamine
Pärast sageduse selekteerimist vajavad vastuvõetud signaalid sageli täiendavat võimendamist, kuna raadiosignaalid võivad olla väga nõrgad. Mähised aitavad võimendamise protsessis mitmel viisil.
A. Võimendustrafod:
- Raadiovastuvõtjates ja saatjates kasutatakse mähiseid tihti trafodena, et võimendada või muuta signaali pinge taset. Trafosid kasutatakse signaalide pinge tõstmiseks või langetamiseks sõltuvalt süsteemi vajadustest.
- Kui signaal on väga nõrk, võib primaarmähise magnetväli indutseerida tugevama voolu sekundaarmähises, tõstes seeläbi signaali pinge taset. See on oluline eriti AM- ja FM-raadiovastuvõtjates, kus signaale tuleb tugevdada enne nende töötlemist ja muutmist kuuldavaks heliks.
B. Suurenenud signaalikvaliteet:
- Mähised aitavad ka signaale stabiliseerida ja võimendada, vähendades müra ja häireid. See võimaldab vastuvõetaval signaalil olla puhtam ja täpsem, mis parandab vastuvõtja üldist jõudlust ja tagab parema kuulamiskogemuse.
Resonantsi loomine raadiosageduste jaoks
Resonants on raadiosüsteemide jaoks äärmiselt oluline. Mähised aitavad luua resonantssagedusi, mis on vajalikud teatud raadiosageduslike signaalide täpseks eraldamiseks ja võimendamiseks. Resonants võimaldab vastuvõtjal töötada täpselt selle sagedusega, mida soovitakse kuulata või saata, samal ajal kui kõik teised sagedused blokeeritakse või ignoreeritakse.
A. Vastuvõtjates:
- Vastuvõtjad kasutavad resonantsahelaid, et häälestuda kindlale sagedusele, näiteks konkreetsele raadiojaamale või saatjale. Mähis LC-ahelas aitab täpselt valida selle sageduse, kus signaal on kõige tugevam ja puhtam. Kuna raadiovastuvõtjate antennid püüavad kinni palju erinevaid sagedusi, aitab resonants neilt soovitud sagedust eristada.
B. Saatjates:
- Raadiosaatjad kasutavad resonantsi, et edastada signaale kindlal sagedusel. See tagab, et signaalid edastatakse täpselt määratud sagedusel, vältides segadust teiste sagedustega ja võimaldades saatjal edastada täpse signaali valitud vahemikus.
Kasutamine raadio ja raadiosageduslikes rakendustes
Mähised on olulised mitte ainult traditsioonilistes AM- ja FM-raadiotes, vaid ka paljudes muudes raadiosageduslikes rakendustes, nagu:
- Mobiilsides: Mähised aitavad mobiilsidesüsteemides selekteerida ja võimendada erinevaid sagedusi, mida kasutatakse andmeside edastamiseks.
- Wi-Fi ja Bluetooth-seadmetes: Need seadmed kasutavad sarnaseid sageduse selekteerimise ja võimendamise tehnikaid mähiste ja kondensaatorite abil.
- Saatjate ja vastuvõtjate antennides: Antennides, mis edastavad ja vastuvõtavad signaale, kasutatakse mähiseid signaali kvaliteedi ja tugevuse parandamiseks.
Kokkuvõte
Mähised on raadiovastuvõtjates ja -saatjates hädavajalikud komponendid, mis aitavad valida ja võimendada signaale. Mähised moodustavad koos kondensaatoritega LC-resonantsahelaid, mis võimaldavad süsteemil häälestuda kindlatele sagedustele, jättes kõrvale kõik teised sagedused. Pärast soovitud sageduse valimist aitavad mähised ka signaali võimendada, et seda oleks lihtsam töödelda ja edastada. Tänu nendele omadustele on mähised kriitilise tähtsusega raadiosageduskommunikatsioonis ja paljudes muudes elektroonikaseadmetes.
4. Trafo põhimõte ja mutuaalne induktsioon
Kahe või enama mähise vahel võib tekkida mutuaalne induktsioon, kus ühe mähise magnetväli indutseerib teises mähises voolu. Seda põhimõtet kasutatakse trafodes, mis võimaldavad pinget tõsta või langetada, samuti energia ülekandmiseks ühest ahelast teise ilma füüsilise ühenduseta.
5. Elektromagnetid (solenoidid)
Mähised võivad luua tugeva magnetvälja, kui vool läbib neid, ning neid kasutatakse elektromagnetides, näiteks releedes, elektrimootorites ja generaatorites.
Lineaarliikumisega solenoid
Lineaarliikumisega solenoidil (Joonis) on kolm tähtsat tunnust: käigupikkus, jõud ja töötsükkel.
Käigupikkus on kaugus kuhu solenoidi südamik liigub.
Jõudu võib defineerida liikumise alguses liikumises, lõppedes või kogu liikumise jooksul. Jõud on alguses väiksem kui liikumise lõpus.
Töötsükkel on väljendatud protsendina (Näitab kui suure osa moodustab sisselülitamisaeg kogu tsükli ajast.)
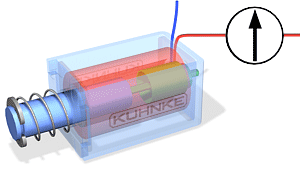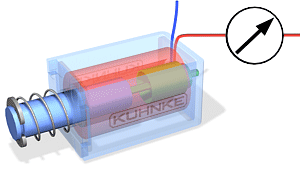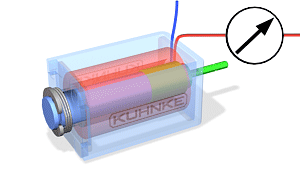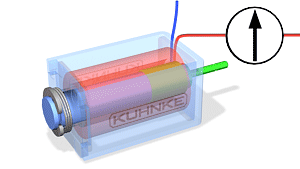
Kahe suunalised lineaarliikumisega solenoidid
Kahe suunalised lineaarliikumisega solenoidid.
Kahesuunalised lineaarliikumisega solenoidid puhul kasutatakse tavaliselt kahte erineva polaarsusega mähist.
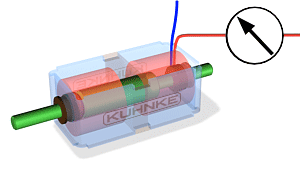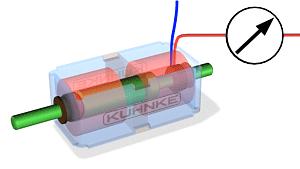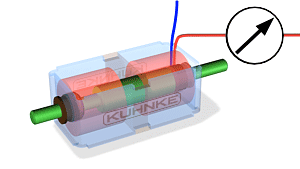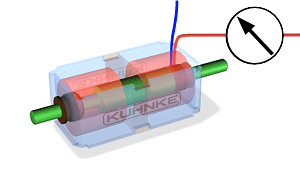
Bistabiilsed solenoid
Bistabiilsel solenoidil on kaks stabiilset positsiooni, solenoidmähise konstruktsioonis on püsimagnetid, mis võimaldavad südamikul kindla positsiooni säilitada ka pärast elektriimpulssi. Perspektiivis on bistabiilsel solenoidil kaks stabiilset seisundit. Esiteks- kui solenoidile on elektriliselt rakendatud ja südamik on täielikult väljas ja teiseks – kui solenoid on ilma vooluta ning südamik fikseeritakse püsimagnetitega (Joonis 3.4)
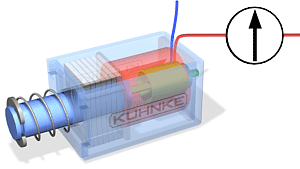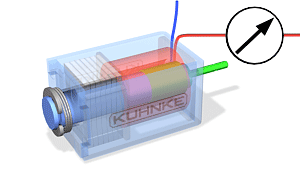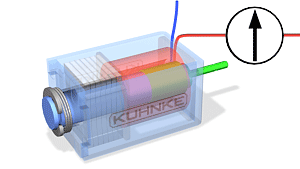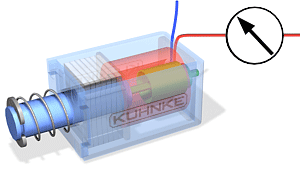
Pöördliikumisega solenoidid
Põhiliselt kasutatakse kahte tüüpi pöördliikumisega solenoide:
Ühesuunalise pöördliikumisega solenoidid (solenoidmähisest arendatav jõud on ühesuunaline ja tagastust toimub mehaaniliselt, kõige sagedamini vedruga).
Kahesuunalise pöördliikumisega solenoidid (kasutatakse kahte pooli, – kiirendust muudetakse keerdude arvuga)


Ühesuunalise pöördsolenoide maksimaalne pöördenurk on reeglina 95 ° ja kahesuunalise pöördsolenoidi pöördenurgad ei ületa 45 °. Automaatikas kasutatakse suhteliselt arva ka suurema pöördenurgaga pöördsolenoide.
Hoidesolenoidid ehk hoidemagnetid
Hoidesolenoidid ehk hoidemagnetid on ilma liikuva südamikuta elektromagnetid, mis omavad suurt hoidejõudu (alates 250 kg hoidejõuga magneteid kasutatakse uste sulgemiseks … üle 700 kg hoidejõuga magneteid kasutatakse turvalukkudes)

Olulised parameetrid
Mähise toimivust ja omadusi mõjutavad mitmed parameetrid:
- Induktiivsus (L) – mõõdetakse henrites (H). Suur induktiivsus tähendab, et mähis suudab rohkem energiat magnetvälja kujul salvestada.
- Maksimaalne voolutugevus – määrab, kui palju voolu mähis suudab taluda ilma ülekuumenemiseta või füüsilise kahjustuseta.
- Tööpiirkond (sagedusvahemik) – sõltuvalt südamiku materjalist ja konstruktsioonist võib mähis olla sobilik kas madala või kõrge sagedusega signaalide jaoks.
- Mähise takistus – mähise traadil on ka teatav elektriline takistus, mis võib põhjustada soojuskaod.
Kokkuvõte
Induktiivpool ehk mähis on elektroonikas ja elektrotehnikas oluline komponent, mille põhifunktsiooniks on energia salvestamine magnetvälja kujul ning voolu muutuste takistamine. Mähised on hädavajalikud nii energiat salvestavates vooluahelates, signaalide töötlemises kui ka pinge ülekandmises trafo kaudu. Erinevad mähise tüübid on kohandatud eri rakenduste jaoks, pakkudes optimaalset lahendust vastavalt kasutusvaldkonnale ja nõuetele.
Induktiivpool
Induktiivpool (lühidalt: pool) on elektroonikakomponent, mida kasutatakse elektriahelates võnkeringide ja filtrite induktiivelemendina. Pooli põhiline tunnussuurus on elektriline induktiivsus.
Induktiivpooli, millega vähendatakse koormusahelas voolu vahelduvkomponenti või tõkestatakse teatud sagedusest kõrgemate sageduskomponentide edasipääsu, nimetatakse paispooliks ehk drosseliks.

Ehitus



Pool koosneb alusest ja sellele mähitud mähisest. Alusele mähitud poolidel võib olla üks või mitu mähist. Samuti võivad ühe mähise osad olla alusele mähitud sektsioneeritult, ühekihilised mähised kindla keerusammuga.
Väikese induktiivsusega poolide puhul võib poolialus ka puududa. Kõrgsageduspoolid, mis on mähitud jämedast vask- või hõbetatud traadist, võivad olla ka ilma aluseta (mähitud vastava jämedusega alusele ja seejärel alus eemaldatud).
Selleks et vähendada pooli mõõtmeid ja võimaldada induktiivsust teatud piirides sujuvalt reguleerida, kasutatakse suurt magnetilist läbitavust omavat ferriitsüdamikku. Ülikõrgsageduspoolides kasutatakse diamagnetilisest metallist (nt vasest) südamikke; need mõjuvad induktiivsust vähendavalt.
Parasiitsidestuste tekkimise vältimiseks varjestatakse induktiivpoolid vask- või alumiiniumplekist varjega.
- Mitmesuguseid induktiivpoole
- Raadiosageduspoole
(all: ferriitantenn kesk- ja pikklainele) - Lameda ferriitsüdamikuga pool trükilülitusele
- Induktiivkomponendid (värvimarkeeringuga)
Mähiste liigid
Pooli mähise kuju ja mähkimisviisi alusel eristatakse järgmisi mähiseid:
- ühe- ja mitmekihiline tihemähis – mähitakse keerd keeru kõrvale ja vajadusel mähisekihid üksteise peale;
- samm-mähis – mähitakse traadi läbimõõdust suurema keerusammuga;
- sektsioonmähis – koosneb ühisele pikiteljele või alusele mitmest jadamisi mähitud ja omavahel ühendatud mähiseosast;
- ristmähis – mähise naaberkihtides olevad mähisekeerud on omavahel mähitud mingi nurga all;
- vabamähis – mähitakse vabalt (korrapäratult) aluse otsketaste ehk põskede vahele;
- sümmeetriline mähis – saadakse kahe juhtmega korraga mähkimisel, kui ühe juhtme lõpp ühendada teise juhtme algusega, ühendamiskoht on mähise keskharund ehk keskväljaviik.

Induktiivpooli tunnussuurused ja aseskeem
- Induktiivsus
on võrdeline mähise keerdude arvu ruuduga ning sõltub ka mähise kujust ning südamiku materjalist;
- Hüvetegur
on pooli induktiivtakistuse
ja poolis tekkiva kõrgsagedustakistuse
suhe:
;
- Omamahtuvus
sõltub mähise keerdudevahelisest hajumahtuvusest
;
- Induktiivsuse temperatuuritegur
näitab induktiivsuse suhtelist muutumist temperatuurimuutumisel 1 K võrra.
Kaotakistuste ja omamahtuvuse tõttu kujuneb Induktiivpooli või drosseli aseskeemmitmekomponendiliseks.
Südamikuta induktiivpoolid
Järgmiste valemite abil saab võrdlemisi täpselt arvutada südamikuta pooli induktiivsust ja keerdude arvu. Kõigis valemites on induktiivsus mikrohenrides (μH) ja poolide mõõtmed millimeetrites.
Ühekihiline tihemähisega induktiivpool
Ühekihilise tihemähisega induktiivpoole kasutatakse enamasti sagedusel üle 500 kHz. Mähis võib olla mähitud poolialusele tihedalt keerd keeru kõrvale või suurendatud sammuga, s.t mähis mähitakse traadi diameetrist suurema sammuga; mähise keerdude vahele jäävad siis vahed. Suurendatud sammuga poolid on väikese omamahtuvuse ja suure hüveteguriga (

Ühekihilise pooli induktiivsus
kus
‒ pooli keerdude arv;
‒ keeru läbimõõt, s.o poolialuse läbimõõdu
ja traadi läbimõõdu
summa;
‒ mähise pikkus.
Sellesama valemiga saab arvutada ka samm-mähisega ühekihilise pooli (solenoidi) induktiivsuse. Mähise samm
Kui on tarvis leida nõutava induktiivsuse 



Mitmekihiline induktiivpool
Mitmekihilise pooli induktiivsus
kus
‒ mähise keerdude arv;
‒ mähise keskmine läbimõõt;
‒ mähise pikkus;
‒ mähise kõrgus.
Traadi kindla pikkuse korral saadakse suurima induktiivsusega pool sel juhul, kui 

Et mähise mõõtmed olenevad keerdude arvust, ei saa neid mõõtmeid täpselt ette anda. Seepärast tuleb keerdude arv leida järkjärgulise lähendamise teel: arvutada orienteeriv keerdude arv mähise eeldatavate mõõtmete alusel, siis täpsustada mõõtmeid 

Lamemähisega induktiivpoolid
Lamemähisega induktiivpoolid on omadustelt võrreldavad ühekihiliste samm-mähisega poolidega. Neil trükimenetlusel valmistatavatel poolidel on väike omamahtuvus, suur hüvetegur ja stabiilsed parameetrid. Lamemähisega poolid on harilikult ring- või ruutspiraalse kujuga. Järgmistes arvutusvalemites on induktiivsus mikrohenrides ja mõõtmed millimeetrites.
Ringspiraalse lamepooli induktiivsus

Nõutava induktiivsuse saamiseks vajalik ringspiraalse pooli keerdude arv
Nendes valemites
– kujutegur, mis saadakse suhte
alusel diagrammilt;
– pooli suurim välisläbimõõt (mm);
– pooli väikseim siseläbimõõt (mm).
Spiraali moodustavate poolringide tsentrite vahe 


Ruutspiraalse lamepooli induktiivsus
Nõutava induktiivsuse saamiseks vajalik ruutspiraalse pooli keerdude arv
Nendes valemites
– kujutegur, mis saadakse suhte
alusel diagrammilt;
– pooli suurim küljepikkus väljast (mm);
– pooli väikseim küljepikus seest (mm).
Südamikuga induktiivpoolid
Magnetsüdamikud
Kõrgsageduspoolide ja –drosselite valmistamisel kasutatakse pehmemagnetferriiti, varem ka magnetodielektrikuid, näiteks karbonüülrauda. Pehmemagnetferriidid, välja arvatud mangaantsinkferriit, on kasutatavad üldiselt nõrgas magnetväljas.
Ferromagnetilisi südamikke iseloomustab
- efektiivne magnetiline läbitavus
‒ südamikuta pooli induktiivsuse ja samasuguse südamikuga pooli induktiivsuse suhe;
- südamiku hüvetegur – kaonurga tangensi
pöördväärtus; mida suurem on südamiku kaoenergia, seda väiksem on selle hüvetegur;
- südamiku parameetrite stabiilsus – seda väljendab magnetilise läbitavuse temperatuuritegur, mis võrdub südamiku efektiivse magnetilise läbitavuse suhtelise muutusega temperatuuri muutumisel ühe Kelvini kraadi võrra.
Induktiivpoolidele valmistatakse ferriidist varrassüdamikke, plaatsüdamikke, keermestatud häälestussüdamikke, keermestatud plastpeaga häälestussüdamikke, ferriidist rõngas- ehk toroidsüdamikke, karbonüülrauast ja ferriidist ummis- ehk mantelsüdamikke.
Ferriitsüdamikuga poolid
Silindrilise ferriitsüdamikuga poolidel on suur hüvetegur ja väiksemad mõõtmed kui südamikuta poolidel. Südamiku kasutamisel poolis nõrgeneb pooli puisteväli, samuti lihtsustub pooli häälestamine.
Südamikuga pooli induktiivsus
Ferriidist rõngassüdamikuga induktiivpoolid
Ferriidist rõngassüdamikku kasutatakse, kui on vaja minimaalsete mõõtmete juures maksimaalset induktiivsust. Rõngassüdamikuga poolide eeliseks on väike magnetvoo hajumine, puuduseks suhteliselt keeruline mähkimine ja induktiivsuse sujuva reguleerimise võimaluse puudumine.
Rõngassüdamikuga pooli induktiivsus (mikrohenrides):
kus
– südamiku materjali dünaamiline magnetiline läbitavus,
– südamiku ristlõike pindala (ruutsentimeetrites),
– magnetjõujoonte keskmine pikkus (sentimeetrites),
Pooli keerdude arv
kus
– pooli vajalik induktiivsus (µH),
– rõnga välisläbimõõt (mm),
– rõnga siseläbimõõt (mm),
– südamiku materjali suhteline magnetiline läbitavus,
– südamiku kõrgus (mm).
Mantelsüdamikuga induktiivpoolid
Mantelsüdamikuga poolidele on omane suur hüvetegur ja varjestusaste ning väike omamahtuvus. Südamiku konstruktsioonist tulenev magnetvarjestustoime ei välista vajadusel elektrostaatilist varjestamist.
Mantelsüdamikuga poolide induktiivsus arvutatakse samamoodi nagu silindrilise südamikuga pooli korral.
Diamagnetsüdamikuga induktiivpoolid
Diamagnetsüdamikuga induktiivpoolidel on induktiivsuse vähendamiseks mittemagnetilisest metallist (vask, alumiinium, valgevask) südamik. Diamagnetsüdamikuga on võimalik induktiivsust vähendada 10…15%. Mittemagnetiline südamik vähendab oluliselt pooli hüvetegurit. Kõige väiksemad kaod on puhtast vasest südamiku korral. Teistest metallidest südamike kasutamisel suureneb kadu võrdeliselt vase elektritakistuse ja kasutatava metalli elektritakistuse suhtega.
Induktiivpoolide varjestus
Poolide varjestamist kasutatakse neil juhtudel, kui on vaja ära hoida poolidevahelist parasiitsidestust. Parasiitsidestust tekitab poolide ümber olev magnetväli.
Varje mõjul väheneb pooli induktiivsus ja hüvetegur ning suureneb omamahtuvus. Pooli andmete muutumine on seda suurem, mida lähemal on varje pooli mähise keerdudele.
Poolide varjestamiseks kasutatakse alumiinium-, vask- või valgevaskplekist silindrilisi või ristkülikukujulisi topsikuid. Sageli tehakse kõrgsageduspoolide varjetesse avad, et oleks võimalik keerata häälestamiseks poolisüdamikke.
Dioodid

- Sümbol:
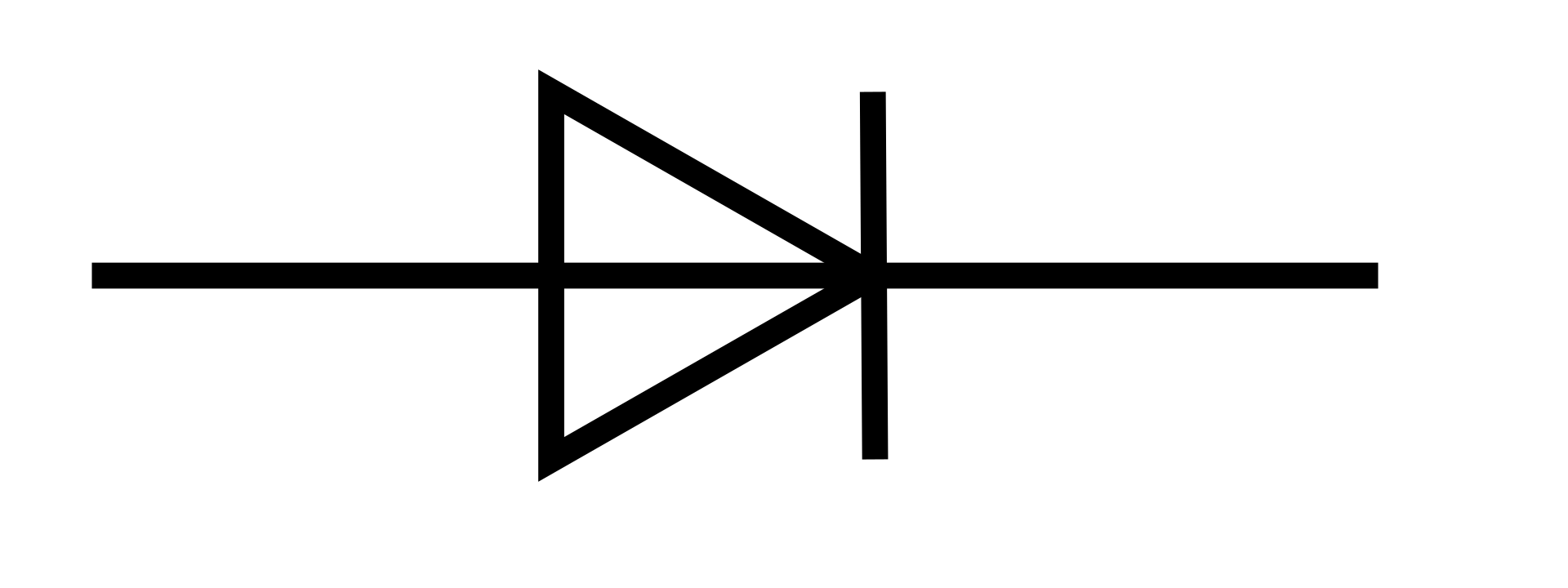
- Kirjeldus: Diood laseb elektrivoolul voolata ainult ühes suunas. Seda kasutatakse voolu suuna kontrollimiseks ja alaldi vooluringides.
- Tähis: D või VD
Mis on diood?
Diood on elektrooniline komponent, mis laseb elektrivoolu voolata ainult ühes suunas. See on valmistatud pooljuhtmaterjalidest, tavaliselt ränist (Si) või germaaniumist (Ge). Dioodi üks peamisi omadusi on selle asümmeetriline juhtivus, mis tähendab, et see juhib voolu ainult etteantud suunas.
Dioodi ülesehitus
Diood koosneb kahest pooljuhtkristallist:
- P-pooljuht (positiivne pool): sisaldab augke, mis on positiivsed laengukandjad.
- N-pooljuht (negatiivne pool): sisaldab elektrone, mis on negatiivsed laengukandjad.
P-N-siirde kohas tekib nn depletsioonikiht, kus augud ja elektronid kombineeruvad, luues elektrivälja, mis takistab edasist laengute liikumist.
Dioodi P-N-siire ja selle tööpõhimõte
1. P-N-siirde mõiste
Diood koosneb kahest erinevast pooljuhtmaterjalist: P-tüüp ja N-tüüp. Need kaks moodustavad P-N-siirde, mis on dioodi südames.
- P-tüüp pooljuht: Pooljuhtmaterjal, mis sisaldab valdavalt positiivseid laengukandjaid ehk auke. Augud on tekkinud tänu sellele, et P-tüüpi materjalile lisatakse spetsiaalseid lisandeid, näiteks boori, mis annab materjalile ühe vähem elektroni kui tavaline räniaatom. Selle tulemusena tekivad positiivsed laengukandjad ehk augud.
- N-tüüp pooljuht: Pooljuhtmaterjal, mis sisaldab valdavalt elektrone ehk negatiivseid laengukandjaid. N-tüüpi pooljuhtmaterjalile lisatakse lisandeid, näiteks fosforit, mis annab materjalile ühe elektroni rohkem kui tavaline räni. See tekitab elektronide ülejäägi, muutes materjali negatiivselt laetud laengukandjateks.
2. P-N-siirde moodustamine
Kui P-tüüpi ja N-tüüpi pooljuhtmaterjalid pannakse kokku, moodustub nendevaheline kontaktpiirkond, mida nimetatakse P-N-siirdeks. Alguses toimub laengukandjate difusioon:
- Elektronid N-tüübist liiguvad P-tüüpi piirkonda, kus nad kombineeruvad aukudega.
- Augud P-tüübist liiguvad N-tüüpi piirkonda, kus nad kombineeruvad elektronidega.
Selle protsessi tulemusena tekib depletsioonikiht, kus elektronid ja augud neutraliseerivad üksteise laengu. Selles piirkonnas pole enam vabasid laengukandjaid ja seega ei saa seal elektrivool vabalt liikuda.
3. Depletsioonikiht ja elektriväli
Depletsioonikihi piirkonnas tekib sisseehitatud elektriväli. Elektronide ja aukude liikumise tõttu jääb N-tüüpi piirkond positiivseks (sest elektronid on lahkunud) ja P-tüüpi piirkond negatiivseks (sest augud on liikunud välja). See tekitab elektrivälja, mis takistab laengukandjate edasist difusiooni P-N-siirdes.
Sisuliselt käitub P-N-siire takistusena, mis ei lase voolu läbi, välja arvatud siis, kui dioodile rakendatakse sobiv pinge.
4. Dioodi töörežiimid
Edasisuunaline siire (Forward Bias):
- Kui P-pool on ühendatud positiivse ja N-pool negatiivse pingega, siis sisseehitatud elektriväli nõrgeneb. Positiivne pinge tõmbab elektronid N-tüüpi piirkonnast P-tüüpi piirkonda ning augud liiguvad vastassuunas, põhjustades depletsioonikihi kahanemise. Kui rakendatud pinge ületab depletsioonikihi elektrivälja barjääri, hakkab vool liikuma. See juhtub siis, kui pinge on vähemalt
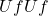 (edaspingelangus), mis ränidioodil on umbes 0,7 V.
(edaspingelangus), mis ränidioodil on umbes 0,7 V.
Tagasisuunaline siire (Reverse Bias):
- Kui P-pool on ühendatud negatiivse ja N-pool positiivse pingega, siis sisseehitatud elektriväli tugevneb, mis laiendab depletsioonikihti veelgi ja takistab laengukandjate liikumist. Sellises seisundis voolu läbi dioodi praktiliselt ei voola. Kui aga tagurpidi pinge muutub piisavalt suureks (ületab läbilöögipinge), hakkab diood voolu läbi laskma, mis võib põhjustada kahjustusi või dioodi hävimise.
5. P-N-siirde matemaatiline kirjeldus
Dioodi edasisuunalise voolu saab arvutada Shockley dioodivõrrandi abil:![]()
Kus:
- II on edasisuunaline vool dioodis.
- IS on dioodi küllastusvool (väga väike vool, mis voolab tagasisuunalises siires).
- UD on pinge dioodi üle.
- nn on ideaalitustegur (tavaliselt väärtusega 1 kuni 2).
- UT on soojuspinge, mis on umbes 26mV toatemperatuuril.
6. P-N-siirde füüsikaline mõistmine
P-N-siiret võib mõista kui ventiili, mis lubab elektrivoolu läbi voolata ainult ühes suunas. Kui diood on edasisuunas pingestatud, liiguvad laengukandjad vabalt läbi P-N-siirde ja vool saab läbi dioodi voolata. Tagasisuunas pingestamisel aga depletsioonikiht laieneb, muutes P-N-siirde elektriliselt mittejuhtivaks, kuni pinge saavutab ohtliku läbilöögitaseme.
7. P-N-siirde ja dioodi rakendused
P-N-siirde tööpõhimõtte põhjal kasutatakse dioode mitmesugustes elektroonilistes rakendustes, sealhulgas:
- Alaldi vooluringides (AC muundamine DC-ks).
- Ülepinge kaitse seadmetes, kus dioodid kaitsevad vooluringi liigpingete eest.
- Signaali demoduleerimine, näiteks raadio vastuvõtjates, kus kasutatakse dioode signaali eraldamiseks.
Kas see lahti seletus aitab hästi mõista P-N-siirde põhimõtteid ja kas peaksime lisama näidisülesandeid või graafikuid?
Dioodi tööpõhimõte
Diood töötab sõltuvalt sellest, kuidas ta on ühendatud vooluahelasse.
- Edasisuunaline siire (Forward Bias): Kui P-pool on ühendatud positiivse ja N-pool negatiivse pingega, ületatakse depletsioonikihi barjäär, laengukandjad hakkavad liikuma, ja vool saab läbi dioodi voolata.
- Tagasisuunaline siire (Reverse Bias): Kui P-pool on ühendatud negatiivse ja N-pool positiivse pingega, siis depletsioonikiht laieneb ja takistab voolu läbiminekut. Sellisel juhul on diood “blokeeritud”.
Edasisuunaline siire (Forward Bias): Kui P-pool on ühendatud positiivse ja N-pool negatiivse pingega, siis väheneb depletsioonikiht ja vool saab läbi dioodi liikuda. Valem edasisuunalise voolu arvutamiseks:
![]()
Kus:
![]() on dioodi vool,
on dioodi vool,
![]() on küllastusvool,
on küllastusvool,
![]() on dioodi pinge,
on dioodi pinge,
![]() on ideaalitustegur (tavaliselt vahemikus 1-2),
on ideaalitustegur (tavaliselt vahemikus 1-2),
![]() on soojuspinge
on soojuspinge ![]() .
.
Tagasisuunaline siire (Reverse Bias): Kui P-pool on ühendatud negatiivse ja N-pool positiivse pingega, siis depletsioonikiht laieneb ja takistab voolu. Kui tagasisuunaline pinge ületab läbilöögipinge ![]() , hakkab diood voolu läbi laskma ja võib kahjustuda.
, hakkab diood voolu läbi laskma ja võib kahjustuda.
Dioodi olulised parameetrid
- Edaspingelangus (Forward Voltage)
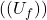 : See on pinge, mille juures diood hakkab juhtima. Ränidioodidel on see tavaliselt 0,7V, germaaniumdioodidel 0,3V.
: See on pinge, mille juures diood hakkab juhtima. Ränidioodidel on see tavaliselt 0,7V, germaaniumdioodidel 0,3V. - Tagurpidi läbilöögipinge (Reverse Breakdown Voltage)
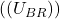 : Kui diood on ühendatud tagurpidi ja pinge ületab teatud taseme, hakkab diood voolu läbi laskma, mis võib põhjustada dioodi kahjustuse.
: Kui diood on ühendatud tagurpidi ja pinge ületab teatud taseme, hakkab diood voolu läbi laskma, mis võib põhjustada dioodi kahjustuse. - Maksimaalne vool (Maximum Current)
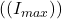 : Dioodi kaudu võib läbida maksimaalselt lubatud vool ilma, et see üle kuumeneks ja häviks.
: Dioodi kaudu võib läbida maksimaalselt lubatud vool ilma, et see üle kuumeneks ja häviks.
Dioodide tüübid
- Tavaline diood: Põhifunktsiooniks voolu juhtimine ühes suunas.
- Zenerdiood: Mõeldud töötama tagurpidi siires ja kasutatakse pinge stabiliseerimiseks.
- LED (Light Emitting Diode): Diood, mis emiteerib valgust, kui vool voolab edasisuunas.
- Schottky diood: Madalama pingelangusega diood, kasutatakse suure kiirusega vooluringides.
- Fotodiood: Diood, mis genereerib voolu vastuseks valgusele.
Alustame siis detailse õppematerjali kirjutamist, lisades valemeid ja näidisülesandeid.
Dioodide tüübid ja omadused
- Zenerdiood: Pinge stabiliseerimiseks kasutatakse Zenerdioode, mis töötavad tagurpidi ja hoiavad pinge konstantse pärast läbilöögipinge saavutamist. Zenerdioodi kasutamisel pinge stabiliseerimiseks kehtib valem:
![Rendered by QuickLaTeX.com \[U_{out} = U_Z\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-14e47282ecab9281e890db66847fdecc_l3.png)
Kus: 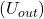 on väljundpinge,
on väljundpinge,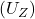 on Zenerdioodi läbilöögipinge.
on Zenerdioodi läbilöögipinge.- LED (valgusdiood): Diood, mis emiteerib valgust edasisuunalises siires. Valgusdioodidel on kõrgem edaspingelangus kui tavalistel dioodidel (tavaliselt 1.8–3.3V).
Näidisülesanded
Näidisülesanne 1: Edasisuunaline vool
Leidke edasisuunaline vool tavalise ränidioodi puhul, kui dioodile on rakendatud pinge ![]() ja küllastusvool
ja küllastusvool ![]() .
.
Lahendus:
Kasutame dioodi edasivoolu valemit:
![]()
Toatemperatuuril on ![]() . Oletame, et
. Oletame, et ![]() (tüüpiline väärtus ränidioodile).
(tüüpiline väärtus ränidioodile).
Arvutame:
![]()
Ligikaudne tulemus:
![]()
Seega on dioodi kaudu voolav vool ligikaudu 1 mA.
Näidisülesanne 2: Zenerdiood
Zenerdiood on ühendatud vooluahelas tagurpidi ning sellele on rakendatud pinge ( 12V ). Zenerdioodi läbilöögipinge on ( 5.6V ). Arvutage väljundpinge.
Lahendus:
Zenerdioodi tööpõhimõtte järgi stabiliseerib ta väljundpinge oma läbilöögipinge tasemel, mistõttu:
![]()
Rakendused
- Alaldises (rectifiers): Dioodid muundavad vahelduvvoolu (AC) alalisvooluks (DC), näiteks toiteplokkides.
- Pinge stabiliseerimisel: Zenerdioodid hoiavad teatud pinge väärtuse stabiilsena.
- Signaalide tuvastamisel: Dioode kasutatakse erinevate signaalide (nt raadiosignaalide) eraldamiseks ja tuvastamiseks.

Dioodi iseloomustav graafik
Dioodi voolu ja pinge suhet saab illustreerida graafikuna, kus:
- Edaspingelangus on punkt, mille juures diood hakkab juhtima.
- Läbilöögipinge on punkt, kus diood hakkab juhtima vastassuunas.
Võime joonistada ka dioodi I-V karakteristikuid ja lisada joonistused selgitamaks selle erinevaid töörežiime.
LED (Valgusdiood)

- Sümbol:
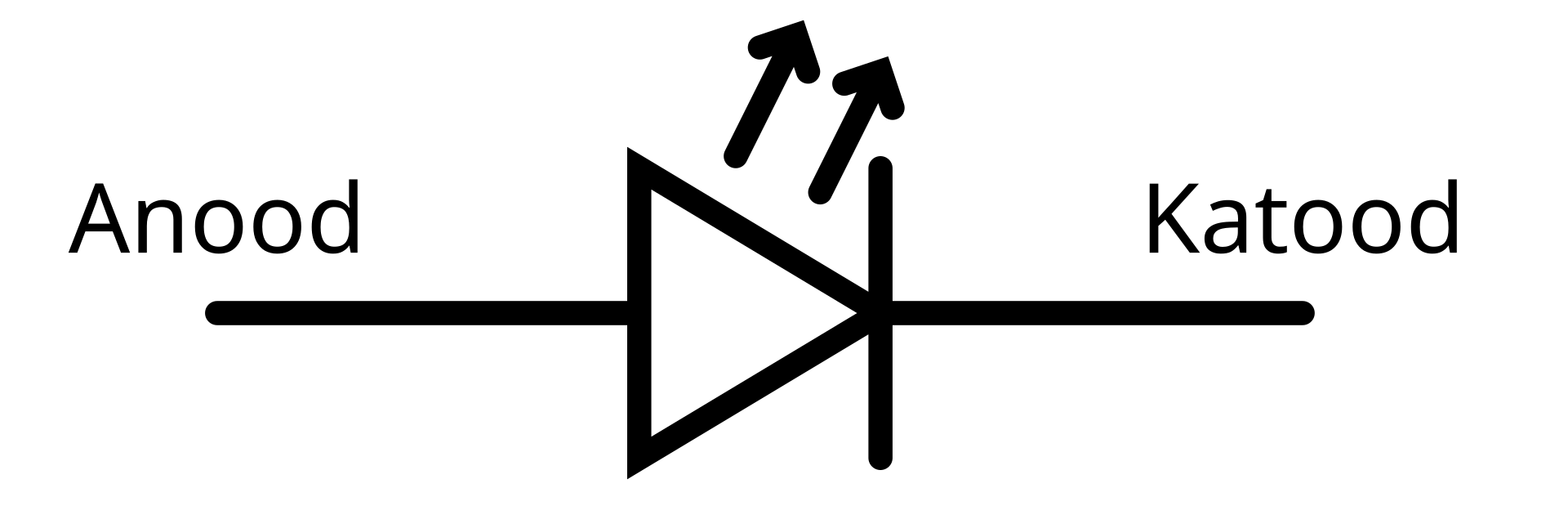
- Kirjeldus: LED on diood, mis kiirgab valgust, kui selle kaudu voolab vool. Seda kasutatakse valgustamiseks ja indikaatoritena.
- Tähis: D või LED
Mis on valgusdiood (LED)?
Valgusdiood ehk LED (Light Emitting Diode) on pooljuhtseade, mis emiteerib valgust, kui läbi selle voolab elektrivool. LED erineb tavalisest dioodist selle poolest, et kui edasisuunaline vool voolab läbi dioodi, vabanevad elektronid ja augud oma rekombinatsioonil energia valgusena. See valgus võib olla erinevat värvi sõltuvalt pooljuhtmaterjalist ja selle lisanditest.
LEDi tööpõhimõte
LED töötab edasisuunalise siirde põhimõttel, sarnaselt tavalise dioodiga:
- Kui LEDi P-pool on ühendatud positiivse ja N-pool negatiivse pingega, hakkavad elektronid ja augud rekombineeruma P-N-siirdes. Selle rekombinatsiooni käigus vabaneb energia valgusena. Välja kiiratud valguse lainepikkus (ja seega ka värvus) sõltub kasutatud pooljuhtmaterjalist.
Erinevad pooljuhtmaterjalid tekitavad erinevaid valgusvärve. Näiteks:
- Galliumarseniid (GaAs): infrapuna
- Galliumarseniid-fosfiid (GaAsP): punane või kollane valgus
- Indiumgaalium-nitriid (InGaN): sinine või roheline valgus
LEDi töökarakteristikud
Valgusdioodi kõige olulisemad parameetrid on:
- Edaspingelangus
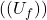 : LEDil on tavaliselt kõrgem edaspingelangus kui tavalisel dioodil. Tüüpilised väärtused on:
: LEDil on tavaliselt kõrgem edaspingelangus kui tavalisel dioodil. Tüüpilised väärtused on:
- Punased LEDid:
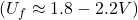
- Rohelised ja sinised LEDid:
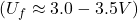
- Punased LEDid:
- Maksimaalne vool
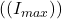 : LED vajab stabiilset voolu, et vältida ülekuumenemist ja kahjustamist. Tüüpiliselt on LEDi töövool vahemikus 10 mA kuni 30 mA.
: LED vajab stabiilset voolu, et vältida ülekuumenemist ja kahjustamist. Tüüpiliselt on LEDi töövool vahemikus 10 mA kuni 30 mA.
Takisti arvutamine LEDi jaoks
LEDi vooluahelas on vajalik takisti, et piirata voolu ja vältida LEDi kahjustamist. Takisti suurus sõltub LEDi edaspingelangusest, toitepingest ja soovitud voolust.
Takisti arvutamiseks saab kasutada Ohmi seadust:
![]()
Kus:
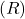 on takisti väärtus (oomides),
on takisti väärtus (oomides),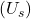 on toitepinge (voltides),
on toitepinge (voltides),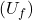 on LEDi edaspingelangus (voltides),
on LEDi edaspingelangus (voltides),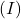 on soovitud vool (amprites).
on soovitud vool (amprites).
Näide takisti arvutamiseks
Näidisülesanne:
Oletame, et meil on punane LED, mille edaspingelangus ![]() on 2.0V ja soovime seda kasutada vooluahelas, kus toitepinge
on 2.0V ja soovime seda kasutada vooluahelas, kus toitepinge ![]() on 9V. Soovime, et LEDi kaudu voolaks vool
on 9V. Soovime, et LEDi kaudu voolaks vool ![]() (või 0.02A).
(või 0.02A).
Lahendus:
Kasutame Ohmi seadust:
![]()
Seega vajame takistit väärtusega 350 Ω, et piirata voolu ja kaitsta LEDi.
Kui täpselt sellist takistit pole saadaval, siis valime kõige lähedasema suurema väärtuse, näiteks 360 Ω, et tagada LEDi kaitse.
LEDi omadused ja piirangud
LEDi projekteerimisel tuleb arvestada järgmiste omaduste ja piirangutega:
- Edaspingelangus on värviti erinev: Seega erinevate värvide LEDid vajavad erinevaid takisteid, et töötada samas pingega vooluahelas.
- Voolupiirang on oluline: Kui LEDile lasta liiga suur vool, võib see üle kuumeneda ja hävida.
- Pinge stabiliseerimine: Kuna LEDi edaspingelangus võib temperatuurist sõltuvalt muutuda, kasutatakse stabiilse voolu tagamiseks mõnikord täiendavaid vooluallikaid või stabilisaatoreid.
Näidisülesanne erinevate LEDide kasutamisel
Ülesanne: Vooluahelas, kus toitepinge on 12V, kasutatakse kahte LEDi: üks punane ![]() ja üks sinine
ja üks sinine ![]() , ning soovime, et mõlemad LEDid töötaksid 15 mA vooluga. Arvutage vajalike takistite väärtused.
, ning soovime, et mõlemad LEDid töötaksid 15 mA vooluga. Arvutage vajalike takistite väärtused.
Lahendus punase LEDi jaoks:
![]()
Valime lähima suurema takisti väärtuse, mis on 680 Ω.
Lahendus sinise LEDi jaoks:
![]()
Valime lähima suurema takisti väärtuse, mis on 600 Ω.
Rakendused
Valgusdioode kasutatakse laialdaselt erinevates rakendustes:
- Valgustus: LEDid on muutunud populaarseks tänu oma energiasäästlikkusele ja pika eluea tõttu. Neid kasutatakse kodudes, tänavavalgustites ja autotööstuses.
- Signalisatsioon ja märgutuled: LEDid on kompaktsed ja saadaval erinevates värvustes, mis teeb neist ideaalsed komponendid märgutuledes ja signalisatsioonisüsteemides.
- Elektroonikaseadmete ekraanid: LEDid on levinud mobiiltelefonide, arvutiekraanide ja televiisorite taustvalgustuses.
Kas soovid lisada täiendavaid näidisülesandeid või graafikuid LEDide kohta?
Järgmine tabel[3] annab ülevaate suurema levikuga valgusdioodide värvidest ja nende valmistamiseks kasutatavatest pooljuhtmaterjalidest. Lisaks on toodud välja ka lainepikkuste vahemikud ja kasutatavad pinged.
| Diood | Värv | Lainepikkus nm | Pinge V | Pooljuht |
|---|---|---|---|---|
 | Infrapunane | λ > 760 | ΔV < 1,9 | Galliumarseniid (GaAs) Alumiiniumgalliumarseniid (AlGaAs) |
 | Punane | 610 < λ < 760 | 1,63 < ΔV < 2,03 | Alumiiniumgalliumarseniid (AlGaAs) Galliumarseniidfosfiid (GaAsP) Alumiiniumgalliumindiumfosfiid (AlGaInP) Gallium(III)fosfiid (GaP) |
 | Oranž | 590 < λ < 610 | 2.03 < ΔV < 2.10 | Galliumarseniidfosfiid (GaAsP) Alumiiniumgalliumindiumfosfiid (AlGaInP) Gallium(III)fosfiid (GaP) |
 | Kollane | 570 < λ < 590 | 2,10 < ΔV < 2,18 | Galliumarseniidfosfiid (GaAsP) Alumiiniumgalliumindiumfosfiid (AlGaInP) Gallium(III)fosfiid (GaP) |
 | Roheline | 500 < λ < 570 | 1,9 < ΔV < 4,0 | Indiumgalliumnitriid (InGaN) / Gallium(III)nitriid (GaN) Gallium(III)fosfiid (GaP) Alumiiniumgalliumindiumfosfiid (AlGaInP) Alumiiniumgalliumfosfiid (AlGaP) |
 | Sinine | 450 < λ < 500 | 2,48 < ΔV < 3,7 | Tsinkseleniid (ZnSe) Indiumgalliumnitriid (InGaN) Ränikarbiid (SiC) substraadina Räni (Si) substraadina – (arendusjärgus) |
 | Violetne | 400 < λ < 450 | 2,76 < ΔV < 4,0 | Indiumgalliumnitriid (InGaN) |
 | Lilla | mitu liiki | 2,48 < ΔV < 3,7 | kahekordne sinine/punane LED, sinine ja punase luminofooriga või valge lilla korpusega |
 | Ultravioletne | λ < 400 | 3,1 < ΔV < 4,4 | Teemant (C) (235 nm) Boornitriid (BN) (215 nm) Alumiiniumnitriid (AlN) (210 nm) Alumiiniumgalliumnitriid (AlGaN) Alumiiniumgalliumindiumnitriid (AlGaInN) – (210 nm) |
 | Valge | lai spekter | ΔV = 3,5 | Sinine / UV-diood kombineeritud kollase luminofooriga |
Transistor

- Sümbol:
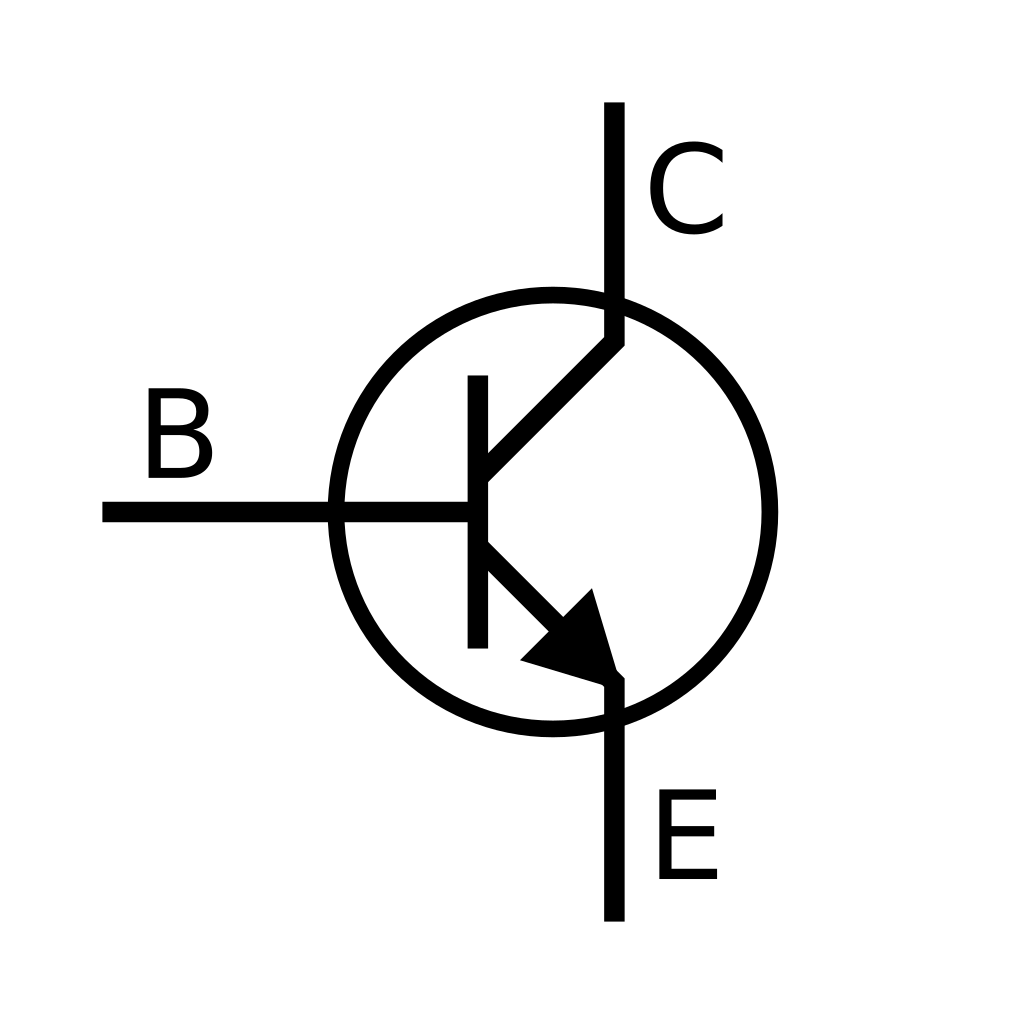
- Kirjeldus: Transistor toimib lüliti või võimendina. Seda kasutatakse signaalide võimendamiseks ja vooluringide juhtimiseks.
- Tähis: Q
BJT (Bipolaarne ühendtransistor) on üks levinumaid transistoreid, mis koosneb kahest erineva tüüpi pooljuhikihist, mis on ühendatud kas n-p-n või p-n-p struktuuriks. BJT-sid kasutatakse voolu võimendamiseks ja lülititena.
BJT struktuur

BJT struktuuris on kolm peamist osa:
- Kollektor (C)
- Baasi (B)
- Emitter (E)
Olenevalt struktuurist võivad need kihid olla kas n-tüüpi või p-tüüpi pooljuhtmaterjalid. BJT võib olla kas n-p-n või p-n-p struktuuriga.
1. n-p-n transistor:
- Kollektor: Ülemine kiht, mis on valmistatud n-tüüpi pooljuhist ja on laiem kui emitteri ja baasi kihid. Kollektor võtab vastu elektrone (voolukandjad) emitterilt läbi baasi.
- Baas: Õhuke p-tüüpi pooljuhtmaterjal, mis asub kollektor- ja emitterikihi vahel. Kuna baasikiht on väga õhuke ja nõrgalt legeeritud, võimaldab see enamikul voolu kandvatel elektronidel läbida baasi ja jõuda kollektorini, tekitades tugeva voolu.
- Emitter: Alumine kiht, mis on valmistatud n-tüüpi pooljuhist ja tugevasti legeeritud. Emitter on tugevasti legeeritud, et toota suurt hulka elektrone, mida saab baasi kaudu juhtida kollektorisse.
Tööpõhimõte:
- n-p-n transistori töö põhineb elektronide liikumisel. Kui baasile rakendatakse väikest positiivset pinget (võrreldes emitteriga), voolavad elektronid emitterilt läbi baasi ja jõuavad kollektorisse, tekitades voolu. Kuna baas on väga õhuke, laseb see suurel hulgal elektrone liikuda läbi, muutes transistori heaks võimenduseks.
2. p-n-p transistor:
- Kollektor: Ülemine kiht on p-tüüpi pooljuhtmaterjal, mis võtab vastu auke (positiivsed laengu kandjad) emitterilt.
- Baas: Õhuke n-tüüpi kiht, mis on nõrgalt legeeritud, võimaldades aukude liikumist emitterist kollektorisse.
- Emitter: Alumine kiht on valmistatud p-tüüpi pooljuhtmaterjalist, mis on tugevalt legeeritud, et toota palju auke, mida saab läbi baasi suunata kollektorisse.
Tööpõhimõte:
- p-n-p transistoris liiguvad peamised laengu kandjad (augud) emitterist baasi poole ja sealt edasi kollektorisse. Kui baasile rakendatakse negatiivset pinget, liiguvad augud emitterist läbi baasi kollektorisse ja vool tekitatakse. Selleks, et p-n-p transistor töötaks, peab emitter olema positiivsema potentsiaaliga kui baas.
BJT tööpõhimõte ja karakteristikud:
- Juhtimine: BJT on voolu juhtimisega seade, kus vool, mis kulgeb läbi baasi ja emitteri vahel, kontrollib voolu kollektor-emitteri vahel.
- Kui baasi vool suureneb, suureneb ka kollektorivool (IC).
- Võimendus: BJT kasutab väikest baasi-emitteri voolu (IB) võimendamaks suurt kollektor-emitteri voolu (IC). Transistori voolu võimendustegur on β (või hFE), mis on kollektorivoolu ja baasi voolu suhe: β = IC / IB.
- Küllastus ja katkestus:
- Küllastusrežiim: Kui transistor töötab täielikult juhtivas olekus (suur IB ja suur IC), nimetatakse seda küllastusrežiimiks.
- Katkestusrežiim: Kui transistor on täielikult välja lülitatud ja vool ei läbi seda (IB ≈ 0), on transistor katkestusrežiimis.
BJT struktuuri tööpõhimõtte võrdlus:
- n-p-n transistor: Elektronide liikumine emitterist kollektorisse läbi baasi.
- p-n-p transistor: Aukude liikumine emitterist kollektorisse läbi baasi.
BJT-transistorid on olulised võimendites ja lülitusrakendustes, kus on vaja väikese juhtvoolu abil juhtida suuremaid voolusid.
FET struktuur
FET reguleerib voolu värava pinge abil. See on energiasäästlikum kui BJT.

Välise juhtimisega transistoride (FET – Field Effect Transistor) struktuur põhineb elektrivälja mõjul kanalil voolava voolu juhtimisel. FET-transistoridel on kolm põhielektrilist klemmi: allikas (source, S), tühjendus (drain, D) ja värav (gate, G). Sõltuvalt FET-tüübist (n-kanal või p-kanal) ning kas tegemist on Junction FET-i (JFET) või Metal-Oxide-Semiconductor FET-i (MOSFET)-iga, võivad struktuurid veidi erineda. Allpool on mõlema FET-tüübi põhilised struktuurid:
1. JFET (Junction FET) struktuur
JFET on lihtsaim FET-tüüp, mis koosneb pooljuhist kanalist, mille kaudu voolab vool allika ja tühjenduse vahel. Selle juhtimiseks kasutatakse PN-üleminekut, mis kontrollib kanali laiust.
- n-kanal JFET struktuur:
- Kanal: n-tüüpi pooljuhtmaterjal (n-kanal), mille kaudu voolab elektrivool allikast (S) tühjendusse (D).
- Värav (G): P-tüüpi piirkond (p-tüüpi pooljuht), mis moodustab PN-ülemineku kanali ja värava vahel. Värava kaudu rakendatav pinge kontrollib kanali juhtivust. Negatiivne väravapinge vähendab kanali laiust ja lõpuks lülitab voolu täielikult välja.
- Allikas ja tühjendus: Vool voolab allikast tühjendusse läbi kanali. Väravapinge määrab kanali laiuse ja seega voolu tugevuse.
- Iseloomustus: Pinge värava ja allika vahel (VGS) reguleerib kanali takistust. Mida negatiivsem on VGS, seda rohkem kanal aheneb, kuni vool katkeb.
- p-kanal JFET struktuur on vastupidise polaarsusega, kus kanal on valmistatud p-tüüpi materjalist, ja voolu juhtimiseks kasutatakse positiivset väravapinget.
2. MOSFET (Metal-Oxide-Semiconductor FET) struktuur
MOSFET-i eripära on see, et värav on isoleeritud kanali ja juhtimisstruktuuri vahel õhukese oksiidkihi kaudu, mis muudab selle kõrge sisendtakistusega ja efektiivsemaks võrreldes JFET-iga.
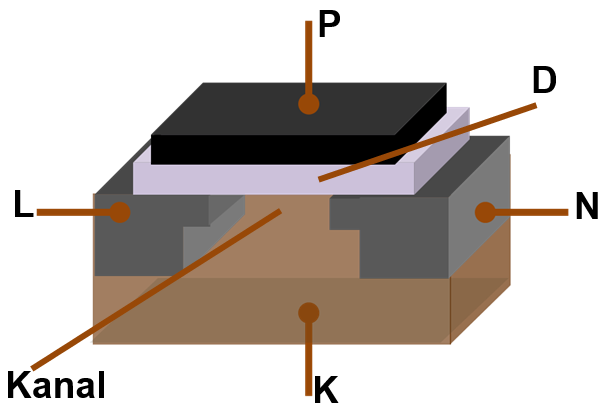
MOSFET – terminoloogia
MOSFET transistori struktuuri kirjelduse terminoloogia:
Pooljuhtplaat (K) – see vastab substraadile või kehale (Substrate või Body). MOSFET on tavaliselt ehitatud räni pooljuhtplaadile, mis moodustab aluse, millesse kanal, allikas ja dreen on sisse ehitatud.
Pais (P) – see vastab väravale (Gate). Pais viitab elektroodile, millele rakendatakse juhtivuse kontrollimiseks pinge. Selle kaudu juhitakse kanali juhtivust. “Pais” viitab eelkõige voolu juhtimisele läbi kanali.
Läte (L) – see vastab allikale (Source). Läte on koht, kust elektronid (või augud) väljuvad ja alustavad oma teekonda läbi kanali. Eesti keeles viitab “läte” allika rollile, mis on voolu lähtemoment.
Neel (N) – see vastab dreenile (Drain). Neel on koht, kuhu vool liigub pärast kanali läbimist. See on transistori elektrood, kus vool lõpeb.
Dielektrik (D) – see viitab oksiidkihile, mis asub värava ja kanali vahel. Dielektrik on isoleeriv materjal, mis eraldab värava elektroodi kanali pooljuhist ja võimaldab väraval juhtida kanali omadusi, rakendades pinget, ilma et värava kaudu vool kulgeks.
Kanali ala – see on kanal, mille kaudu elektronid või augud liiguvad allikast dreeni, kui väravale rakendatakse vastav pinge. Kanali juhtivus sõltub väravale rakendatud pingest.
- n-kanal MOSFET struktuur:
- Kanal: MOSFET sisaldab n-tüüpi või p-tüüpi pooljuhtmaterjalist kanalit, mis on värava all, kuid esialgu on see välja lülitatud. Kanal moodustub ainult siis, kui väravale rakendatakse piisavalt pinget.
- Värav (G): Metallist või pooljuhtmaterjalist elektrood, mis on eraldatud kanalist õhukese isoleeriva kihi (tavaliselt ränioksiid) abil. Kui väravapinge (VGS) on piisavalt positiivne, tõmbab see alla laetud kandjaid (elektrone), moodustades kanali, mis ühendab allika ja tühjenduse.
- Allikas ja tühjendus: Allikas on koht, kust elektronid sisenevad, ja tühjendus on koht, kuhu nad voolavad. Kui kanal on moodustunud, saab vool voolata allikast tühjendusse.
- Iseloomustus: MOSFET-i puhul juhib voolu väravale rakendatav pinge. Kui pinge on alla künnisepinge, kanalit ei moodustu ja vool ei saa voolata. Kui pinge ületab künnise, moodustub juhtiv kanal ja vool saab voolata.
- p-kanal MOSFET struktuur on sarnane n-kanaliga, kuid kasutatakse p-tüüpi kanalit ja juhtivuse saavutamiseks rakendatakse väravale negatiivset pinget.
MOSFET-i ja JFET-i erinevused struktuuris:
- JFET kasutab PN-üleminekuid kanali juhtivuse reguleerimiseks, samas kui MOSFET-is kasutatakse värava all isoleerivat oksiidkihti, mis võimaldab kõrgemat sisendtakistust.
- MOSFET on kergemini juhitav väikeste pingetega ja seda kasutatakse laialdasemalt kõrgema sagedusega ja madalama energiatarbimisega rakendustes.
- JFET-id on tavaliselt vähem keerukad ja odavamad, kuid MOSFET-id on võimsamad ja efektiivsemad suuremate voolude ja pingete korral.
Transistorite struktuuride tundmine võimaldab nende õigesti valimist ja kasutamist vastavalt rakendusele, näiteks lülititena või võimenduskomponentidena erinevates elektroonikasüsteemides.
Transistori kasutamine lülitina
Transistori kasutamine lülitina
Milleks üldse kasutada transistori lülitina, kui saab ka niisama? Milleks kasutada autot, kui saab jala?! Selleks, et kiirust (n.ö) võimendada. Sama on transistoriga. Transistori abil saame lülitada suuri koormusi nii, et läbi lüliti jooksev vool on kümneid, sadu või tuhandeid kordi väiksem, kui lülitatava seadme tarbitav vool. Teise plussina saame lülitamiseks kasutada madalamat (või kõrgemat) pinget, kui on tarbija toitepinge.
Millist skeemi kasutada, kuidas valida õige transistor, kuidas arvutada õiged takistite väärtused? Asjast on lihtsam aru saada, kui on mõni praktiline ülesanne. Oletame, et peame juhtima mikrokontrolleri väljundiga küttekeha.
Väljundi parameetrid:
- Pinge: 5V
- Maksimaalne vool: 20mA (0,002A).
Küttekeha:
- Toitepinge : 12VDC
- Võimsus: 30W
- Vool: 2,5A
Numbritele otsa vaadates on selge, et küttekeha otse kontrolleri väljundisse ühendada ei õnnestu. Või kui päris täpne olla, ühendada õnnestub aga tööle ei hakka. Esimesel lülimisel rikume oma kontrolleri väljundi (tehase suits tuleb välja).
On selge, et peame nüüd mingi lahenduse appi võtma. Üks võimalik lahendus ongi siin transistori kasutamine.
Meil on valida kahe variandi vahel, kas kasutada NPN või PNP transistorit. Allpool on kaks skeemi varianti:
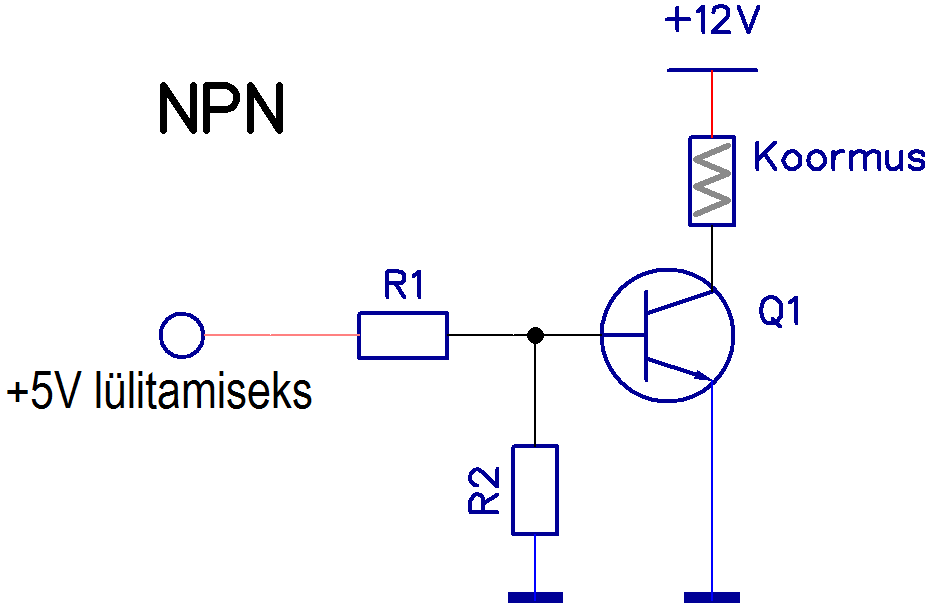
Valige skeemilahendus vastavalt sellele, millist lülimise varianti kasutada soovime. Meie näite puhul valime NPN variandi (parempoolse skeemi), kuna kontrolleri programm on tehtud nii, et kui väljund on aktiivne (1, High), tuleb kütta ja kui passiivne (0, Low) siis ei tohi kütta. Ehk 0V = OFF ja +5V = ON.
Nüüd peame valima sobiliku transistori. Mida on vaja jälgida?
- Lubatud maksimaalne kollektori ja emitteri vaheline pinge (VCE). See ei tohi olla väiksem, kui meil vajalik (tarbija toitepinge 12VDC).
- Kollektori lubatud maksimaalne vool IC. See peab minimaalselt vastama meie vajalikule koormusele (küttekeha tarbitav vool 2,5A).
- Transistori minimaalne võimendustegur hFE Hmm… kui palju see olema peaks? Siin peame natuke arvutama. Lubatud maksimaalne vool, millega me saame transistori lülitada on meil 20mA, selle piirab meile kontrolleri väljund. Mõistlik on siin arvestada turvalise varuga, et mitte väljundit maksimaalselt koormata. Ütleme, et me soovime hakkama saada maksimaalselt 15mA’ga. Tarbija on meil 2,5A ehk 2500mA. See tähendab, et meile vajalik võimendus on 2500 / 15 = 167 korda.
Võtan nüüd ette mõned sahtlis olevad NPN trnasistorid ja otsin välja nende parameetrid. Ehk leian nende hulgast meile sobiliku.
| Tüüp | VCE | IC | hFE |
| 2N2222A | 40V | 0,6A | 35 |
| C3205 | 30V | 2A | 100 |
| C2078 | 75V | 3A | 25 |
| 2SD1222 | 40V | 3A | 1000 |
Nagu eeldada võis on suurema võimsuse ja võimendusega transistorid darlingtoni tüüpi (kaks transistorit ühes korpuses).
Nüüd on meil sobilik transistor olemas ja saame arvutada R1 ja R2 takistite väärtused.
Selleks on meil vaja andmelehelt lisaks hankida transistori baasi ja emitteri vaheline pingelang küllastunud režiimis (VBE (sat) Base-Emitter Saturation Voltage). Rusikareegel on, et ränitransistoritel on see ca 0,6….0,7V ja darlington transistoritel 2x suurem. Meie valitud transistoril 2SD1222 on see 2V.
Nüüd arvutama…
Esmalt peame leidma vajaliku baasi voolu IB.
IB = ILOAD / HFE ehk IB = 2,5A / 1000 = 0,0025A = 2,5mA
R1 = (VB – VBE)/ IB ehk IB = (5V – 2V) / 0,0025A = 1200 Ohm = 1,2kOhm
R2 = R1 x 10 = 12kOhm
Olemas….
Hetkel vedas ja arvutuste vastusteks sattusid takistite standardväärtused. Kui aga nii hästi ei lähe, siis vali esimene lähim madalam standard nominaal.
Teeme ühe praktilise näite veel. Kasutan antennivõimendi ahelasse lülimiseks releesi ja pean lülitama kahte paralleelset releed. Kuna ma ei taha oma raadio esipaneelil olevate kompaktsete mikrolülititega otse relee mähiseid lülitada, otsustasin kasutada transistorit.
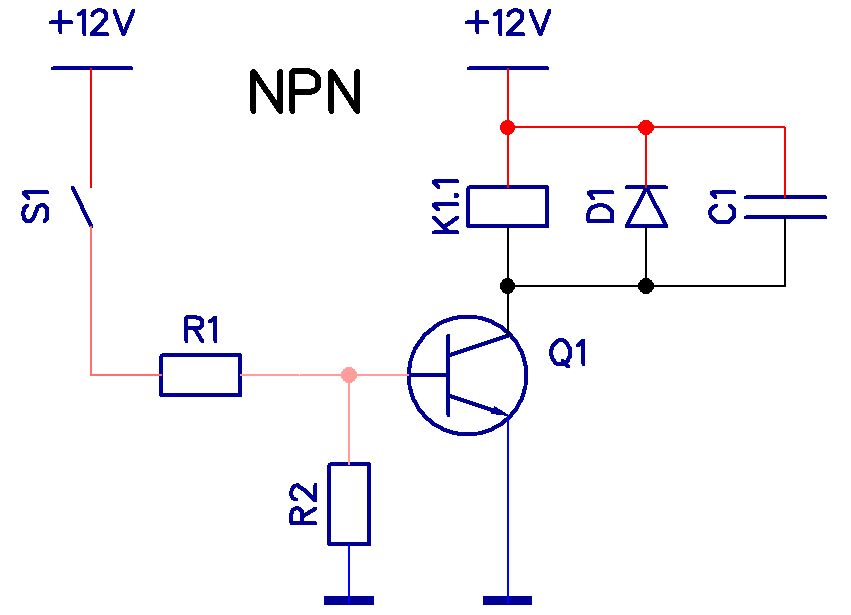
Relee mähise andmed:
- Pinge: 12VDC
- Nimivool: 37,5mA
Transistor
- BC847A

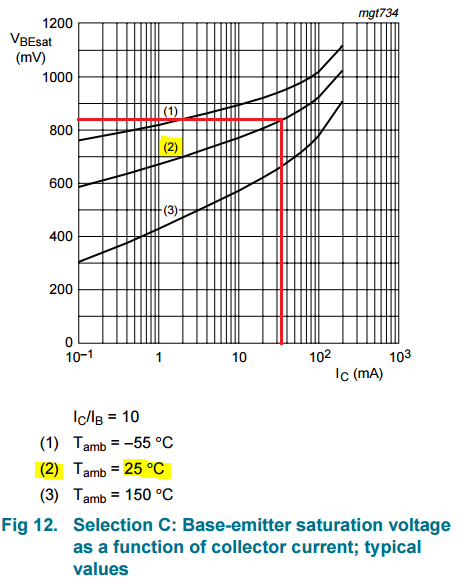
- VCE – 45V
- ICE – 100mA
- hFE – 110
- VBE(sat) – ~0,84V
Ja nüüd arvutama…
IC = 2 x 37,5 = 75mA (0,075A)
IB = Ic / hFE = 0,075A / 110 = 0,00068A (680uA)
R1 = (V – VBE) / IB = (12 – 0,84) / 0,00068 = 16 412 Ohm
Lähim madalam standardväärtus on 15kOhm ja see on meile sobilik.
R2 = R1 x 10 = 150kOhm.
Mõned näpunäited lisaks:
Raadiohäirete vältimiseks võib lisada ka 10…100nF kondensaatori.
Ärge unustage, et suurematel koormustel tuleb tegeleda ka transistori jahutamisega (radiaator, ventilaator).
Kui lülitate induktiivseid koormusi (releed, mootorid jms), siis lisage koormusega paralleelselt diood, et kaitsta transistorit pinge piikide eest, mis tekkivad koormuse lahutamise hetkel.
Transistorite peamised parameetrid ja karakteristikud on olulised nende töö mõistmiseks ja rakendamiseks erinevates elektroonikaseadmetes. Allpool on transistorite peamised parameetrid ja karakteristikud:
1. Voolu võimendus (β või hFE):
- Kirjeldus: See näitab, kui palju transistor suudab võimendada sisendvoolu. Tavaliselt defineeritud kui kollektori voolu (IC) ja baasi voolu (IB) suhe: β = IC/IB.
- Olulisus: Mida suurem on β, seda rohkem võimendab transistor voolu. See parameeter on oluline võimendusahelates, kus transistor suurendab signaali tugevust.
2. Kollektori-vool (IC):
- Kirjeldus: Maksimaalne vool, mida transistor suudab kollektori kaudu juhtida. IC on üks peamistest parameetritest, mis määravad transistoriga töötavate vooluahelate töövõime.
- Olulisus: Kollektori vool määrab, kui palju voolu transistor läbi laseb. See on oluline parameeter toitehaldus- ja lülitusahelates.
3. Kollektor-emitteri pinge (VCE):
- Kirjeldus: Maksimaalne pinge, mida transistor talub kollektor-emitteri vahel, ilma et transistor kahjustuks. Tavaliselt väljendatud kui VCE(max).
- Olulisus: See määrab, millist pinget transistor võib taluda, enne kui see puruneb või lühistub. Oluline toite- ja lülitusahelates, kus transistorid töötavad kõrgepingelistes keskkondades.
4. Sätteläpipinge (VBE):
- Kirjeldus: Minimaalne pinge, mis on vajalik transistori baasi ja emitteri vahel, et transistor lülituks sisse. Tavaliselt on see väärtus umbes 0,6–0,7 V (räni transistorid).
- Olulisus: See määrab, millal transistor hakkab juhtima voolu ja on oluline element lülitus- ja võimendusahelates.
5. Sageduslik piir (fT):
- Kirjeldus: Transistori tööpiir, millel voolu võimendus langeb väärtuseni 1. Tavaliselt väljendatakse MHz või GHz.
- Olulisus: Määrab transistori töövõime kõrgsageduslikes rakendustes, näiteks raadiosagedusahelates ja digitaalses sidevahenduses.
6. Kollektor-emitteri küllastuspingelang (VCE(sat)):
- Kirjeldus: Pinge kollektor-emitteri vahel, kui transistor on täielikult juhtivas (saturatsiooni) olekus. Tavaliselt on see väike, alla 0,3 V.
- Olulisus: Madal küllastuspingelang tähendab väiksemaid energiakadu lülitusahelates, kus transistor töötab lülitina.
7. Leekvool (ICBO):
- Kirjeldus: Väike vool, mis voolab kollektorilt emitterile isegi siis, kui transistor ei ole aktiveeritud (baasi-vool on null). See on oluline parameeter, kui on vaja kõrget täpsust ja vähese lekkevooluga seadmeid.
- Olulisus: Väike lekkevool on oluline madala energiatarbimisega seadmete puhul, näiteks akutoitel töötavate seadmete puhul.
8. Soojusdisipatsioon (PD):
- Kirjeldus: Maksimaalne soojusenergia, mida transistor suudab eraldada, ilma et see kahjustuks. Väljendatud vattides (W).
- Olulisus: See määrab, kui palju võimsust transistor suudab hallata. Kõrge soojusdisipatsioonivõime on oluline võimsusvõimendis ja toiteahelates.
9. Sisendtakistus (hie või Zin):
- Kirjeldus: Transistori sisendi takistus baasi ja emitteri vahel. Tavaliselt on see kõrge, kuid sõltub sagedusest ja voolust.
- Olulisus: Kõrge sisendtakistus on soovitav võimendus- ja signaaliahelates, kuna see vähendab signaali moonutamist.
10. Väljundtakistus (hoe või Zout):
- Kirjeldus: Transistori väljundi takistus kollektori ja emitteri vahel, kui transistor on töörežiimis.
- Olulisus: Madal väljundtakistus on oluline võimendusahelates, et tagada signaali efektiivne edastamine väljundisse.
Transistorite tingmärgid
(lühend inglise k NPN-BJT)
B ‒ baas, C ‒ kollektor, E ‒ emitter
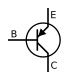
(PNP-BJT)
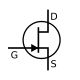
(N-JFET)
G (Gate) ‒ pais, D (Drain) ‒ neel, S (Source) ‒ läte
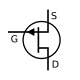
(P-JFET)
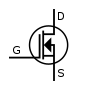
(depletion-mode N-MOSFET)
(sisseehitatud n-kanaliga)
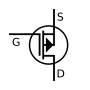
(depletion-mode P-MOSFET)
(sisseehitatud p-kanaliga)

(enhancement-mode N-MOSFET)
(pingestamisel indutseeritava n-kanaliga)
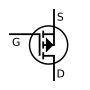
(enhancement-mode P-MOSFET)
(pingestamisel indutseeritava p-kanaliga)
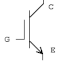
(IGBT)
G ‒ pais, C ‒ kollektor, E ‒ emitter
Toiteallikad
Patareid

- Sümbol:
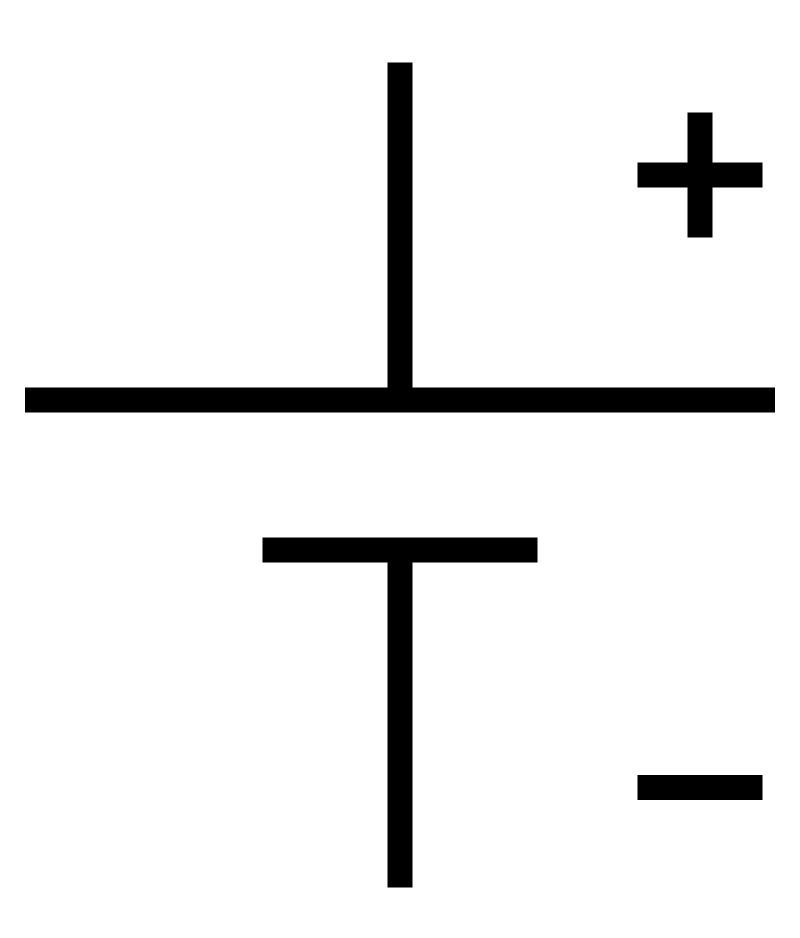
- Kirjeldus: Patarei on vooluallikas, mis tekitab pinge ja juhib elektrivoolu vooluringis.
- Tähis: BT
Toiteallikad, patareid ja akud
Toiteallikad, patareid ja akud on elektriliste seadmete jaoks olulised energiallikad, mis võimaldavad nende töötamist. Allpool on ülevaade nende erinevatest tüüpide ja tööpõhimõtete kohta.

Toiteallikad
Toiteallikad on seadmed, mis teisendavad elektrienergiat ühelt pingetasemelt teisele, et tagada seadmete jaoks sobiv ja stabiilne toide. Toiteallikad jagunevad tavaliselt kaheks tüübiks:
Lineaarsed toiteallikad
- Kirjeldus: Lineaarsetes toiteallikates toimub pinge ja voolu teisendamine pidevalt ja ilma katkestusteta. Need sisaldavad tavaliselt trafo, mis teisendab vahelduvpinge (AC) madalamale pinge väärtusele, millele järgneb alaldi, et muuta see alalisvooluks (DC).
- Omadused:
- Stabiilne väljundpinge.
- Suhteliselt lihtne ehitus.
- Madala müratasemega väljund, mis sobib tundlikule elektroonikale.
- Puudused:
- Madal efektiivsus, kuna üleliigne energia muudetakse soojuseks.
- Suured ja rasked, eriti kõrgema võimsusega rakendustes.
Lülitusrežiimi toiteallikad (SMPS)
- Kirjeldus: SMPS toiteallikad töötavad kõrgel sagedusel, muutes vahelduvvoolu kiiresti sisse ja välja, mis võimaldab kasutada väiksemaid ja kergemaid komponente, näiteks trafosid ja kondekaid.
- Omadused:
- Kõrge efektiivsus, eriti suurema võimsuse korral.
- Kompaktsem ja kergem kui lineaarsed toiteallikad.
- Puudused:
- Suhteliselt keeruline ehitus.
- Suurem müratase (kõrgsageduslik müra), mis võib häirida tundlikku elektroonikat.
Patareid
Patareid on energiasalvestusseadmed, mis teisendavad keemilise energia elektrienergiaks. Patareid jagunevad ühekordseteks (esmased) ja laetavateks (teisased).
Esmased patareid (ühekordse kasutusega)
- Kirjeldus: Esmased patareid on mõeldud ühekordseks kasutamiseks, kuna nende keemiline reaktsioon on pöördumatu. Kui energia on ära kasutatud, tuleb patarei välja vahetada.
- Tüübid:
- Leelispatareid: Kõige tavalisem tüüp igapäeva elektroonikas (näiteks AA, AAA patareid). Kasutavad tsink-anood ja mangaanoksiid-katood.
- Liitium-patareid: Väga suur energiatihedus ja pikk kasutusiga. Sobivad suure energiatarbimisega seadmetesse.
- Omadused:
- Kõrge energiatihedus.
- Hea säilivusaeg ja töökindlus.
- Puudused:
- Ei ole laetavad.
- Patarei lõppedes tuleb see ära visata.
Teisased patareid (laetavad)
- Kirjeldus: Teisased patareid on mõeldud korduvalt kasutamiseks. Nende keemiline reaktsioon on pöörduv, võimaldades neil peale kasutamist elektrienergiat uuesti salvestada.
- Tüübid:
- Liitium-ioon (Li-ion) akud: Kõrge energiatihedus, kerge kaal ja pikk laadimistsükkel. Kasutatakse sülearvutites, nutitelefonides ja elektriautodes.
- Nikkel-metallhüdriid (NiMH) akud: Suure mahutavusega ja keskkonnasõbralikumad kui vanemad NiCd akud. Kasutatakse tavaliselt kaameras ja mängukonsoolides.
- Pliiakud: Suure võimsusega ja odavad, kuid rasked ja mahukad. Levinud autodes ja päikesepaneelide süsteemides.
- Omadused:
- Laetavad ja pikaealised.
- Saab kasutada mitmeid laadimistsükleid (kuni tuhanded tsüklid).
- Puudused:
- Kulukamad kui ühekordse kasutusega patareid.
- Laadimine võtab aega ja mõnel akul esineb mäluefekt (nt vanemad NiCd akud).
Akud
Akud on tegelikult teisased patareid, mida kasutatakse laetavatena suurtes energiatarbimisega süsteemides, nagu elektrisõidukid, varutoite süsteemid ja taastuvenergia lahendused. Nende suur eelis seisneb võimes säilitada suurt kogust energiat ja korduvalt kasutada, kuid nad vajavad ka laadimisseadmeid ja on mahukad.
Liitium-ioon (Li-ion) akud
- Kirjeldus: Kõrge energiatihedusega akud, mis on kerged ja suudavad taluda palju laadimistsükleid. Kasutatakse laialdaselt elektroonikaseadmetes ja elektriautodes.
- Omadused:
- Kerge kaal ja kõrge energiatihedus.
- Ei esine mäluefekti.
- Pikk eluiga (300–500 laadimistsüklit).
- Puudused:
- Kõrgem hind kui traditsioonilised akud.
- Tundlik ülekuumenemise ja ülelaadimise suhtes, mis võib põhjustada ohutusriske.
Pliihappeakud
- Kirjeldus: Vanem tehnoloogia, mis on endiselt laialdaselt kasutusel suurtes rakendustes nagu autod ja päikesepaneelide süsteemid.
- Omadused:
- Madal hind ja suur võimsus.
- Pikaajaline töövõime.
- Puudused:
- Suur kaal ja mahukus.
- Lühike eluiga (200–300 laadimistsüklit).
- Keskkonnale kahjulik (plii ja happe kasutamine).
Nikkel-kaadmium (NiCd) ja nikkel-metallhüdriid (NiMH) akud
- Kirjeldus: Kuigi NiCd akud on olnud traditsioonilised, on NiMH akud neid keskkonnasõbralikkuse ja energiatiheduse tõttu suures osas asendanud.
- Omadused:
- Hea töövõime ka külmades tingimustes.
- NiMH akudel on suurem energiatihedus kui NiCd akudel.
- Puudused:
- NiCd akud kannatavad mäluefekti all.
- NiMH akudel on lühem eluiga kui Li-ion akudel.
Kokkuvõte:
- Toiteallikad annavad stabiilset elektrivoolu seadmete tööks, kusjuures SMPS-toiteallikad on efektiivsemad, aga lineaarsed toiteallikad pakuvad stabiilsemat väljundit.
- Patareid ja akud on energiasalvestusseadmed, kus ühekordse kasutusega patareid sobivad väiksematele seadmetele, ja laetavad akud on vajalikud suurema energiatarbimisega rakendustes, kus korduvalt kasutamine on oluline.
- Akud, nagu Li-ion ja pliiakud, on levinud suure võimsusega süsteemides, kus on vaja pikaajalist ja usaldusväärset energiat.
Lüliti

- Sümbol:

- Kirjeldus: Lüliti katkestab või ühendab vooluringi, võimaldades voolu sisse- ja väljalülitamist.
- Tähis: SW
Lülitid ja nende klassifikatsioon
Lülitid on elektromehaanilised seadmed, mis avavad või sulgevad vooluahelaid, võimaldades elektrivoolul kas voolata läbi ahela või katkestada selle. Lülitite klassifikatsioon põhineb nende funktsioonidel, juhtimisviisidel, konstruktsioonil ja rakendusaladel.
Lülitite klassifikatsioon:
Lüliteid saab jaotada mitmesse kategooriasse nende tööpõhimõtete ja rakenduste alusel:
Töörežiimi põhjal:
- Manuaalsed lülitid: Lülitid, mida käsitsi juhitakse. Näiteks valguslülitid, kus kasutaja füüsiliselt lülitab sisse või välja voolu.
- Automaatlülitid: Lülitid, mis toimivad automaatselt vastavalt eelmääratud tingimustele, näiteks temperatuuri- või rõhuanduritega ühendatud lülitid.
Kontaktide arvu põhjal:
- Ühepooluselised lülitid (Single Pole): Need lülitid suudavad juhtida ühte vooluahelat. Näiteks ühepooluseline ühe viskega lüliti (SPST) suudab avada või sulgeda ainult ühe ahela.
- Kahepooluselised lülitid (Double Pole): Need lülitid kontrollivad kahte sõltumatut vooluahelat korraga. Näiteks kahepooluseline kahe viskega lüliti (DPDT) saab juhtida kaht ahelat ja pakkuda mitut töörežiimi.
asendi arvu põhjal:
- Ühe asendiga lülitid (Single Throw): Ühe asendiga lülititel on ainult üks lülitustee – nad kas avavad või sulgevad ühe ahela. Näiteks SPST lüliti võib ahela kas ühendada või katkestada.
- Kahe asendiga lülitid (Double Throw): Kahe asendiga lülititel on kaks võimalikku lülitustee. Näiteks SPDT (Single Pole Double Throw) lüliti suudab suunata voolu kahele erinevale väljundile.
Kasutusotstarbe põhjal:
- Üldised lülitid: Kasutatakse tavaliselt igapäevaelus, näiteks valgustuslülitid, seadmete sisse- ja väljalülituslülitid.
- Spetsiaalsed lülitid: Kasutatakse konkreetsetes rakendustes, näiteks tööstusautomaatikas või meditsiiniseadmetes. Näiteks ajastatud lülitid või kiirlülitid.
Mehaanika ja tööpõhimõtte põhjal:
- Survelülitid (Push Button Switches): Need lülitid töötavad, kui neid vajutatakse alla (või üles), ning võivad olla hetkelised (nt uksekellad) või püsivad (valguslülitid).
- Kiiklülitid (Rocker Switches): Need lülitid töötavad, kui neid kiigutatakse ühele või teisele poole. Kiiklülitid on sageli levinud koduelektroonikas ja valgustussüsteemides.
- Libistatavad lülitid (Slide Switches): Lülitid, kus kontaktid liigutatakse libistamise teel ühest asendist teise. Kasutatakse sageli väikese elektroonika, näiteks taskulampide ja mänguasjade juhtimisel.
- Pöördlülitid (Rotary Switches): Need lülitid töötavad, kui nende nuppu keeratakse. Pöördlüliteid kasutatakse sageli valiku tegemiseks mitme erineva vooluahela vahel (nt köögitehnika kiiruse valik).
- Mikrolülitid (Micro Switches): Väiksed ja tundlikud lülitid, mis aktiveeruvad väikse liikumise või surve kaudu. Neid kasutatakse sageli täpsetes ja tundlikes rakendustes, näiteks turvalukkudes ja tööstusandurites.
Tööpõhimõtte põhjal:
- Hetkelised lülitid (Momentary Switches): Lülitid, mis jäävad aktiivseks ainult siis, kui neid vajutatakse. Kui vabastada, siis lülitub ahel automaatselt välja. Näiteks uksekell või arvutiklaviatuuri klahvid.
- Püsivad lülitid (Maintained Switches): Lülitid, mis jäävad aktiivseks ka pärast vabastamist, kuni need uuesti välja lülitatakse. Näiteks valguse sisse- ja väljalülitamise lülitid.
Lülitite spetsiaalsed rakendused:
- Jalglülitid: Kasutatakse muusikaseadmetes või tööstuslikes rakendustes, kus käed on hõivatud. Lüliti aktiveerimine toimub jalaga.
- Nutikad lülitid: Elektrooniliselt juhitavad lülitid, mis on ühendatud võrku ja mida saab juhtida kaugelt (nt WiFi-lülitid, nutikodude lülitid).
- Tundlikkuslülitid (Touch Switches): Lülitid, mida aktiveeritakse puudutuse kaudu. Kasutatakse sageli valgustuse ja koduelektroonika juhtimisel.
Populaarsed lülititüübid:
SPST (Single Pole Single Throw) lüliti:
- Üks lülitav kontakt ja üks ahel. Lihtne lüliti, mis katkestab või ühendab ühe vooluahela.
- Näide: Valgustuse sisse-välja lüliti.
SPDT (Single Pole Double Throw) lüliti:
- Üks lülitav kontakt, mis saab ühenduda kahe erineva väljundiga. Seda saab kasutada ühe ahela suunamiseks kahele väljundile.
- Näide: Lüliti, mis vahetab kahe seadme vahel (näiteks ventilaatori kiirus).
DPST (Double Pole Single Throw) lüliti:
- Kahepooluseline lüliti, mis juhib kaht sõltumatut vooluahelat ühe lülituse kaudu.
- Näide: Seade, mis lülitab korraga välja nii faasi kui ka neutraali.
DPDT (Double Pole Double Throw) lüliti:
- Kahepooluseline kahe viskega lüliti, mis juhib kaht vooluahelat ja saab lülitada kahe erineva väljundi vahel.
- Näide: Mootori suuna muutmine elektriahelates.
Lülitite kasutusvaldkonnad:
- Kodumasinad: Valgustite, ventilaatorite, küttekeha lülitamine sisse ja välja.
- Tööstusautomaatika: Kasutatakse masinate ja tööstusseadmete juhtimisel, näiteks konveierilintide või mootorite sisse ja välja lülitamiseks.
- Elektroonikaseadmed: Arvutid, mobiilseadmed, meditsiiniseadmed ja muud täppiselektroonikad, mis vajavad tundlikke ja spetsiifilisi lüliteid.
- Nutikodud: Lülitid, mis on ühendatud koduautomaatikaga ja mida saab juhtida mobiilirakenduste või häälkäsklustega.
Lülitite mõistmine ja nende õige valimine vastavalt rakendusele on kriitiline nii elektroonika, automaatika kui ka igapäeva seadmete puhul, et tagada töökindel ja mugav seadmete juhtimine.
4.2 Skeemide koostamine ja lugemine
Elektriskeemide lugemine ja koostamine hõlmab komponentide sümbolite äratundmist ning nende omavaheliste ühenduste mõistmist. Siin on mõned põhiprintsiibid ja näited.
1. Lihtne vooluring:
Kirjeldus:
Alustame lihtsast vooluringist, mis koosneb patareist, takistist ja LED-lambist. Patarei tekitab pinge, mis põhjustab voolu liikumise läbi takisti ja LED-i, mis siis süttib.
Skeem:
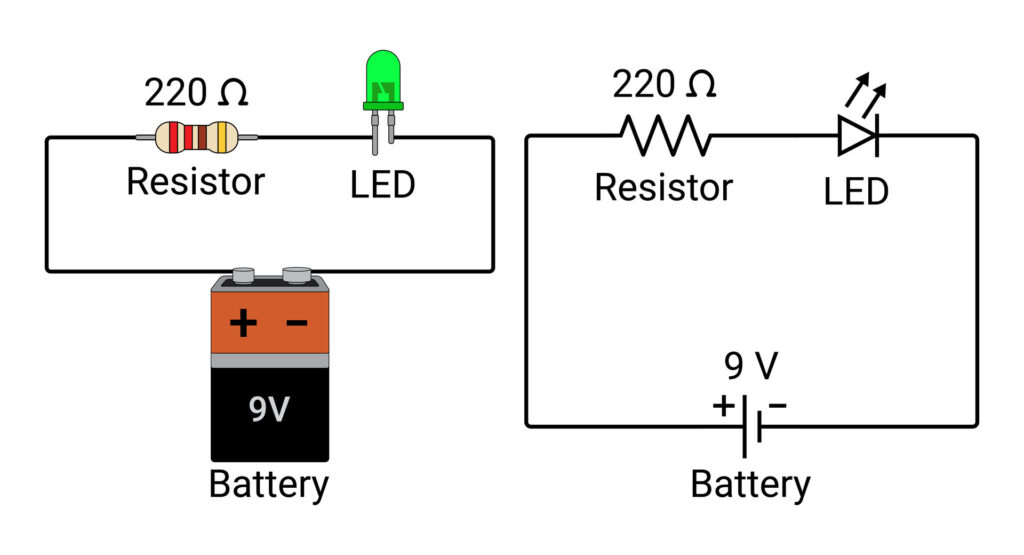
Selgitus:
- Patarei on vooluallikas, mis tekitab pinge vooluringis.
- Takisti piirab voolu, et kaitsta LED-i liigse voolu eest.
- LED süttib, kui vool liigub läbi selle.
2. Vahelduvvoolu vooluring kondensaatori ja induktiivpooliga:
Kirjeldus:
Järgmine näide hõlmab vahelduvvoolu (AC) vooluringi, kus on ühendatud kondensaator ja induktiivpool. Selliseid vooluringe kasutatakse näiteks sagedusfiltrites ja võimendites.
Skeem:
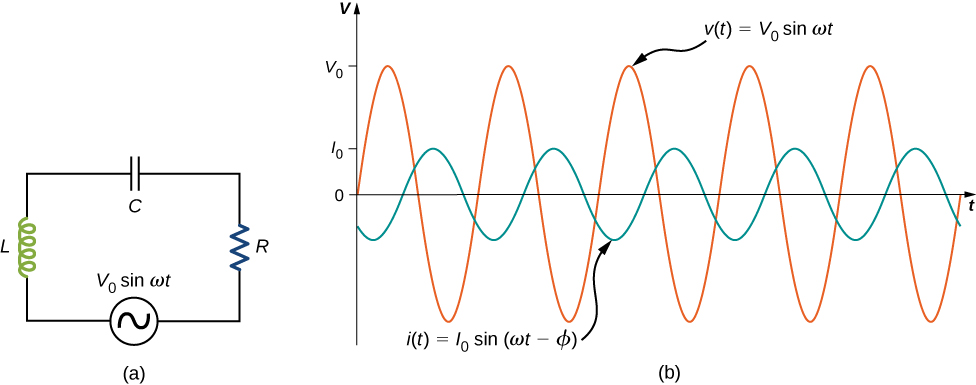
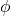 sõltub R, C ja L väärtustest.
sõltub R, C ja L väärtustest.Selgitus:
- Vahelduvvoolu allikas tekitab perioodiliselt muutuvat pinget, mis ajab voolu läbi vooluringi.
- Kondensaator salvestab energiat elektriväljas ja see on seotud vooluringi sagedusomadustega.
- Induktiivpool salvestab energiat magnetväljas ja vastutab samuti sagedusomaduste eest.
3. Transistori kasutamine lülitina:
Kirjeldus:
Selles näites kasutatakse transistori lülitina, et juhtida voolu LED-i kaudu. Kui transistori baasile rakendatakse pinget, avab transistor vooluringi ja LED süttib.
Skeem:
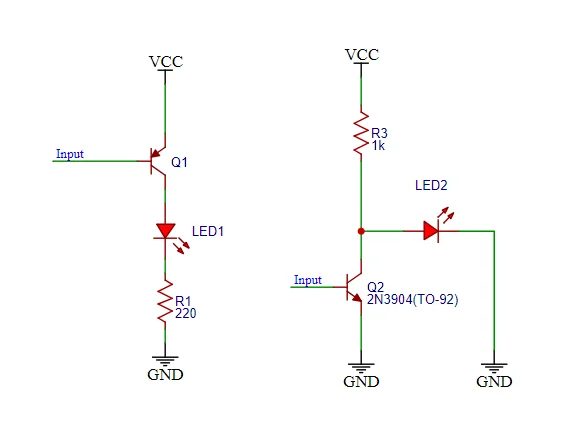
Selgitus:
- Transistor toimib lülitina. Kui lüliti on suletud, rakendatakse transistori baasile pinge, mis võimaldab voolul liikuda kollektorist emitterisse, süüdates LED-i.
- Takisti kontrollib voolu LED-i kaudu, et kaitsta seda kahjustuste eest.
Elektriskeemide lugemine ja koostamine nõuab praktikat ja komponentide sümbolite tundmist. Esitatud skeemid ja nende selgitused aitavad luua arusaama, kuidas erinevad komponendid vooluringis koos toimivad ning kuidas skeeme tõlgendada ja koostada. Skeemide põhjalik mõistmine on kriitilise tähtsusega elektrotehnika ja elektroonika aluste õppimisel ja rakendamisel.
5. Elektriahelate koostamine ja analüüs
Selles peatükis käsitleme põhjalikult elektriliste komponentide, nagu takistid, kondensaatorid, induktiivpoolid ja toiteallikad, jada- ja rööpühendusi. Arutame, kuidas arvutada kogutakistust, mahtuvust, induktiivsust ja pinget erinevates konfiguratsioonides. Toome välja ka näidisülesanded, mis aitavad selgitada jada- ja rööpühenduste praktilist rakendust.
5.1 Jada- ja rööpühenduste põhimõtted
Elektriahelad võivad olla kas jadaühenduses, kus komponendid on ühendatud järjestikku ühes vooluringis, või rööpühenduses, kus komponendid on ühendatud paralleelselt. Jadaühenduses läbib iga komponenti sama vool, kuid pinge jaguneb komponentide vahel. Rööpühenduses jaguneb vool komponentide vahel, kuid pinge jääb kõigis harudes samaks.
5.2 Takistite jada- ja rööpühendused
5.2.1 Takistite jadaühendus

Takistite jadaühenduses summeeruvad kõik takistid lineaarse summana, kuna vool läbib iga takisti järjestikku.
Kogutakistus ![]() :
:
![]()
kus R₁, R₂,… Rₙ on iga jadaühenduses oleva takisti takistus.
Näide 1 (Takistite jadaühendus):
Antud on vooluring, milles on kolm jadaühenduses olevat takistit, väärtustega R₁ = 5 Ω, R₂ = 10 Ω ja R₃ = 20 Ω. Arvutage kogutakistus.
Lahendus:
![]()
Kogutakistus on 35 Ω.
5.2.2 Takistite rööpühendus
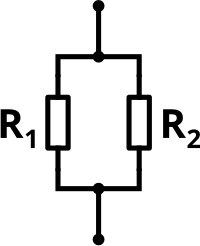
Takistite rööpühenduses voolab iga haru kaudu erinev vool, kuid pinge üle kõikide harude on sama. Kogutakistus arvutatakse pöördsummana.
Kogutakistus ![]() :
:
![]()
Näide 2 (Takistite rööpühendus):
Antud on vooluring, milles on kolm rööpühenduses olevat takistit, väärtustega R₁ = 5 Ω, R₂ = 10 Ω ja R₃ = 20 Ω. Arvutage kogutakistus.
Lahendus:
![]()
![]()
![]()
Kogutakistus on 2.86 Ω.
5.3 Kondensaatorite jada- ja rööpühendused
4.3.1 Kondensaatorite jadaühendus
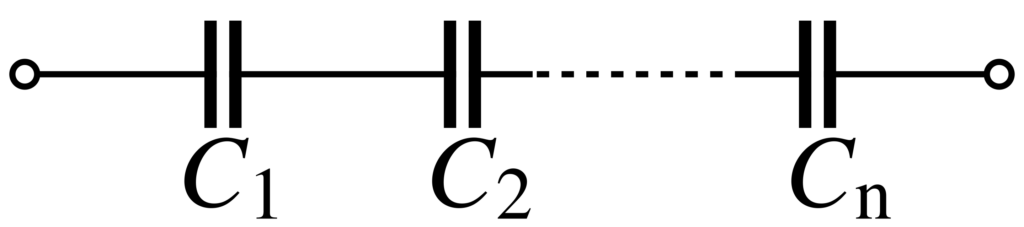
Kondensaatorite jadaühenduses jaguneb mahtuvus pöördvõrdeliselt, kuna pinge üle iga kondensaatori jaguneb.
Kogumahtuvus ![]() :
:
![]()
kus C₁, C₂,… Cₙ on iga jadaühenduses oleva kondensaatori mahtuvus.
Näide 3 (Kondensaatorite jadaühendus):
Antud on vooluring, milles on kolm jadaühenduses olevat kondensaatorit, väärtustega C₁ = 2 μF, C₂ = 4 μF ja C₃ = 8 μF. Arvutage kogumahtuvus.
Lahendus:
![]()
![]()
![]()
Kogumahtuvus on 1.14 μF.
5.3.2 Kondensaatorite rööpühendus
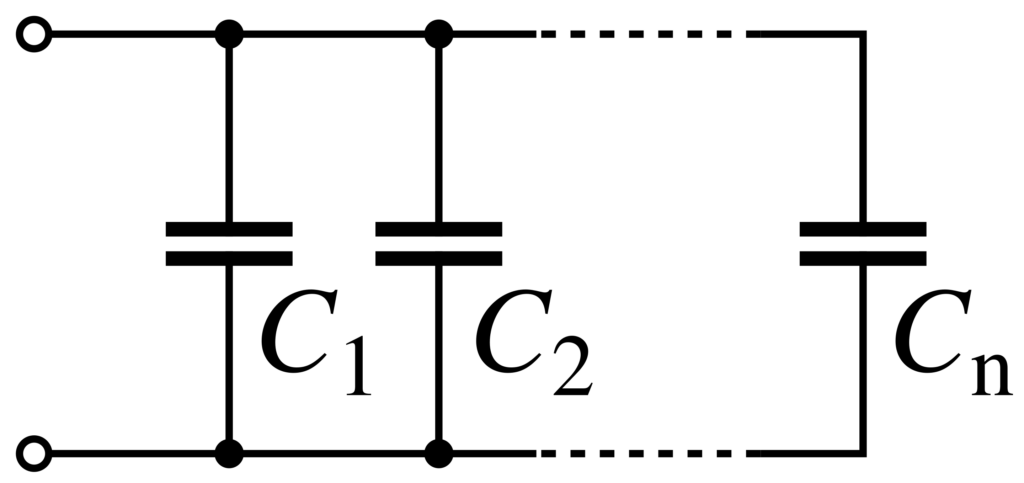
Kondensaatorite rööpühenduses summeerub mahtuvus lineaarse summana, kuna pinge üle kõikide kondensaatorite on sama.
Kogumahtuvus ![]() :
:
![]()
Näide 4 (Kondensaatorite rööpühendus):
Antud on vooluring, milles on kolm rööpühenduses olevat kondensaatorit, väärtustega C₁ = 2 μF, C₂ = 4 μF ja C₃ = 8 μF. Arvutage kogumahtuvus.
Lahendus:
![]()
Kogumahtuvus on 14 μF.
5.4 Induktiivsuse jada- ja rööpühendused
5.4.1 Induktiivpoolide jadaühendus
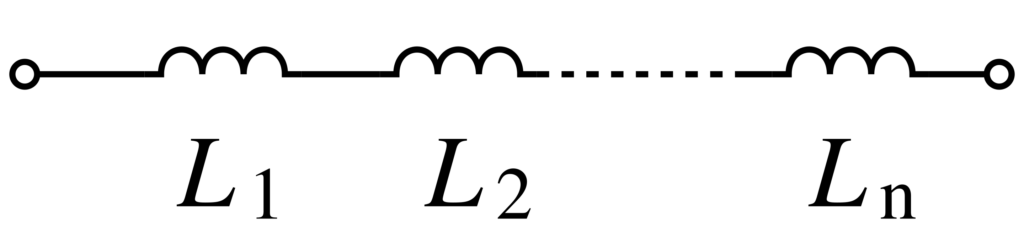
Induktiivpoolide jadaühenduses summeerub induktiivsus lineaarse summana, kuna vool läbib järjestikku kõiki induktiivpooli.
Koguinduktiivsus ![]() :
:
![]()
Näide 5 (Induktiivpoolide jadaühendus):
Antud on vooluring, milles on kolm jadaühenduses olevat induktiivpooli, väärtustega L₁ = 5 mH, L₂ = 10 mH ja L₃ = 15 mH. Arvutage koguinduktiivsus.
Lahendus:
![]()
Koguinduktiivsus on 30 mH.
5.4.2 Induktiivpoolide rööpühendus
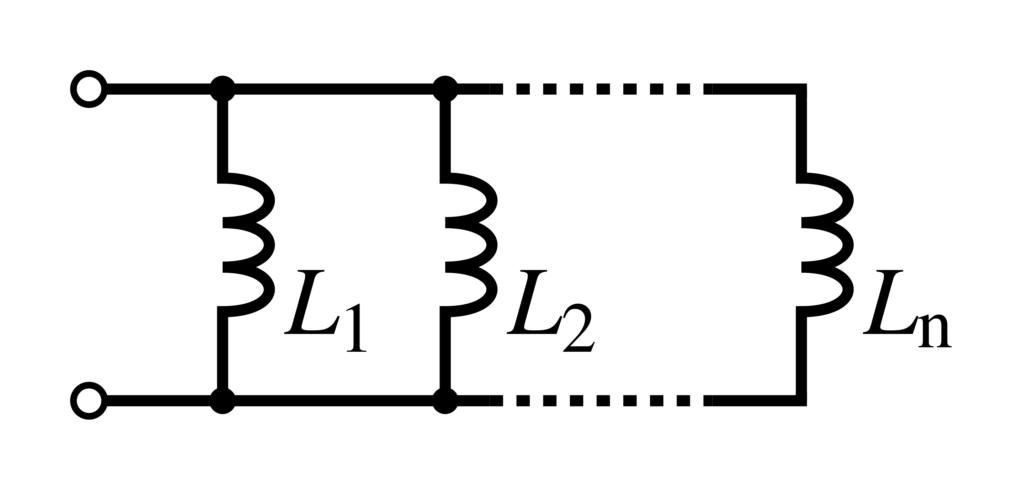
Induktiivpoolide rööpühenduses jaguneb induktiivsus pöördvõrdeliselt, kuna pinge üle iga haru on sama.
Koguinduktiivsus ![]() :
:
![]()
Näide 6 (Induktiivpoolide rööpühendus):
Antud on vooluring, milles on kolm rööpühenduses olevat induktiivpooli, väärtustega L₁ = 5 mH, L₂ = 10 mH ja L₃ = 15 mH. Arvutage koguinduktiivsus.
Lahendus:
![]()
![]()
![]()
Koguinduktiivsus on 2.73 mH.
5.5 Toiteallikate jada- ja rööpühendused
Kui soovid selgitada, kuidas Rohde & Schwarz DC lauaarvuti toiteallikaid saab kasutada jada- või paralleelühenduses, siis siin on lihtne ja arusaadav selgitus:
Toiteallikad võimaldavad kasutajatel samaaegselt reguleerida erinevate väljundite pinget ja voolu. See on kasulik, kui sinu seadmed või katsed nõuavad mitmesuguseid elektrilisi parameetreid.
5.5.1 Toiteallikate jadaühendus
Jadaühenduses lülitatakse mitu toiteallikat järjestikku, et suurendada kogupinget. Näiteks, kui sul on neli toiteallikat, igaüks võimeline andma välja 25 volti, ja ühendad need jadamisi, siis on lõpptulemusena võimalik saavutada 100 volti. See meetod sobib hästi olukordades, kus on vaja kõrgemat pinget, kui üksik allikas suudab pakkuda.
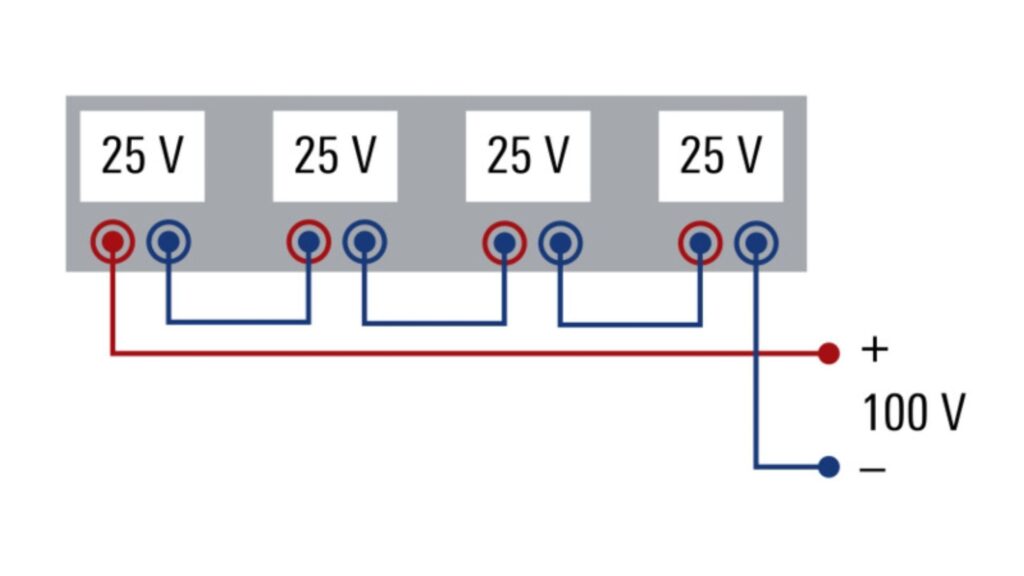
Jadaühenduses summeeruvad toiteallikate pinged, samal ajal kui voolutugevus jääb samaks.
Kogupinge ![]() :
:
![]()
Näide 7 (Toiteallikate jadaühendus):
Antud on kaks jadaühenduses olevat patareid, mille pinged on U₁ = 9 V ja U₂ = 6 V. Arvutage kogupinge.
Lahendus:
![]()
Kogupinge on 15 V.
5.5.2 Toiteallikate rööpühendus
Rööpühenduses ühendatakse toiteallikad kõrvuti, et suurendada koguvoolu. See tähendab, et kui su seadmed vajavad rohkem voolu, kui üks kanal suudab pakkuda, võid ühendada mitu kanalit paralleelselt. See jaotab voolukoormuse mitme kanali vahel, suurendades seeläbi voolutugevust, mida su süsteem suudab kasutada.
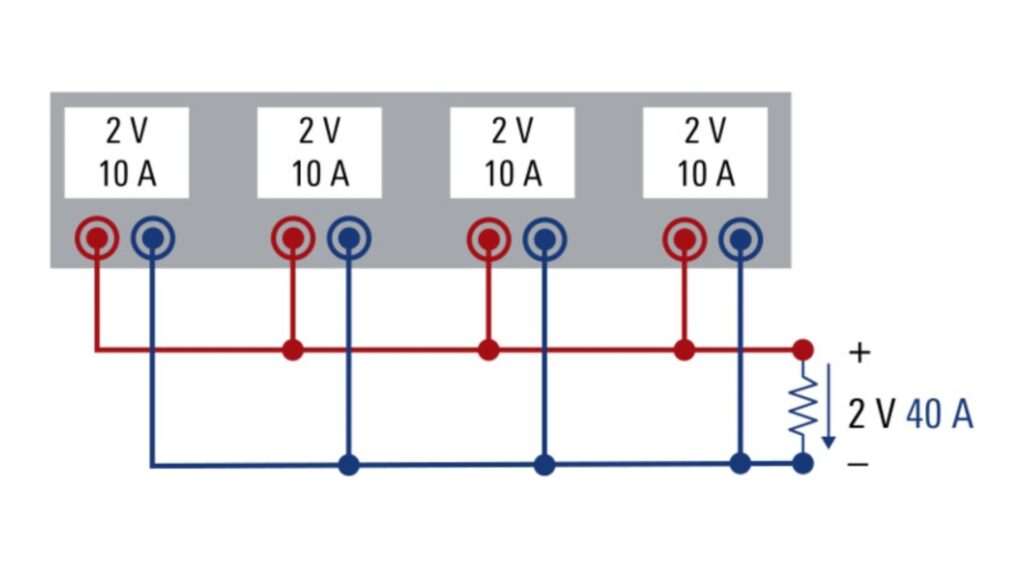
Rööpühenduses summeerub voolutugevus, samal ajal kui pinge jääb samaks.
Kogu voolutugevus ![]() :
:
![]()
Näide 8 (Toiteallikate rööpühendus):
Antud on kaks rööpühenduses olevat patareid, mille voolutugevused on I₁ = 2 A ja I₂ = 3 A. Arvutage koguvoolutugevus.
Lahendus:
![]()
Koguvoolutugevus on 5 A.
Turvalisus ja isolatsioon
On oluline, et kõik ühendused oleksid turvalised. Veendu, et toitekanalid oleksid korralikult isoleeritud. See tähendab, et kanalid ei ole ühendatud ühise maandusega ja iga kanal on elektriliselt sõltumatu. See aitab vältida soovimatut voolu liikumist ühest kanalist teise, mis võib põhjustada seadmete kahjustusi või isegi ohtlikke olukordi.
Selline lähenemine võimaldab väga paindlikku toitesüsteemi kohandamist vastavalt konkreetsetele vajadustele, olgu need siis teadustöös, tootearenduses või muudes tehnilistes rakendustes.
Kui soovid lisateavet või näiteid, külasta Rohde & Schwarz’i veebilehte: Rohde & Schwarz DC Power Supplies.
5.6 Kokkuvõte
Selles peatükis käsitleti põhjalikult takistite, kondensaatorite, induktiivpoolide ja toiteallikate jada- ja rööpühendusi. Toodi välja valemid ja näidisülesanded, mis aitavad paremini mõista, kuidas komponente vooluringis õigesti ühendada ja nende mõju voolule, pingele, mahtuvusele ja induktiivsusele analüüsida.
6. Alalisvoolu ja vahelduvvoolu vooluringid
Elektrotehnika ja elektroonika valdkonnas on kaks peamist elektrivoolu tüüpi: alalisvool (DC) ja vahelduvvool (AC). Need voolutüübid erinevad oma omaduste, rakenduste ja vooluringi disaini poolest. Selles peatükis käsitleme mõlema voolutüübi põhimõtteid, rakendusi ja vooluringi komponente.

6.1 Alalisvoolu põhimõtted
Alalisvool (DC – Direct Current) on elektrivool, mille suund ja tugevus jäävad ajas konstantseks. See tähendab, et elektronid liiguvad pidevalt ühes suunas – tavaliselt negatiivselt positiivse klemmini. Alalisvoolu tekitavad seadmed, mis annavad stabiilset ja muutumatut elektrivoolu. Sellistes vooluringides on ka pinge konstantne ega muutu ajas.
Alalisvoolu allikad:
- Patareid ja akud: Keemiliste reaktsioonide abil tekitatakse elektrivool, mis liigub ühes suunas.
- Päikesepaneelid: Muundavad päikeseenergia elektrienergiaks, andes väljundiks alalisvoolu.
- Alaldid: Muudavad vahelduvvoolu (AC) alalisvooluks, kasutades pooljuhtseadiseid nagu dioodid.
- Alalisvoolugeneraatorid: Toodavad alalisvoolu elektromagnetilise induktsiooni abil.
6.1.1 Alalisvoolu rakendused
Alalisvoolu kasutatakse laialdaselt seadmetes ja süsteemides, kus on vaja stabiilset ja ühtlast elektrivoolu. Peamised rakendused hõlmavad:
- Madalpinge elektroonikaseadmed: Mobiiltelefonid, sülearvutid, tahvelarvutid ja muud kaasaskantavad seadmed kasutavad alalisvoolu, kuna nende komponendid nõuavad stabiilset toiteallikat.
- Akusüsteemid: Akud ja patareid varustavad seadmeid stabiilse alalisvooluga, võimaldades nende iseseisvat tööd ilma võrgutoiteta.
- Sõidukite elektrisüsteemid: Autode ja teiste sõidukite elektrilised süsteemid, sealhulgas valgustus, audioseadmed ja mootorite juhtimissüsteemid, töötavad alalisvooluga.
- Päikeseenergiasüsteemid: Päikesepaneelid toodavad alalisvoolu, mida saab kasutada otse DC-seadmete toiteks või muundada vahelduvvooluks inverterite abil, et toita tavalisi koduseid seadmeid.
- Elektroonika komponendid: Paljud elektroonikakomponendid, nagu transistorid ja integraallülitused, töötavad alalisvooluga.
6.1.2 Alalisvoolu vooluringi komponendid
Alalisvoolu vooluring koosneb mitmest põhikomponendist, mis töötavad koos elektrivoolu juhtimiseks ja kasutamiseks:
- Toiteallikas:
- Patareid või akud: Tekitavad pinge ja juhivad elektrivoolu läbi vooluringi.
- Päikesepaneelid: Toodavad alalisvoolu päikeseenergia muundamisel.
- Juhtmed:
- Elektrijuhtivad materjalid, tavaliselt vask või alumiinium, mis ühendavad vooluringi komponente ja võimaldavad voolu liikumist.
- Takistid:
- Komponendid, mis piiravad voolutugevust, kaitstes teisi vooluringi komponente liigse voolu eest.
- Kasutatakse voolu reguleerimiseks ja pinge jaotamiseks vooluringis.
- Lülitid:
- Seadmed, mis katkestavad või ühendavad vooluringi, võimaldades voolu sisse- ja väljalülitamist.
- Näited: Nupplülitid, kiiklülitid, releed.
- Laadid (koormused):
- Elektrilised seadmed, mis kasutavad voolu töö tegemiseks.
- Näited: LED-lambid, mootorid, elektroonikakomponendid, andurid.
- Muud komponendid:
- Kondensaatorid: Salvestavad elektrilaengut ja siluvad pinge kõikumisi.
- Dioodid: Lubavad voolu voolata ainult ühes suunas, kaitstes vooluringi pöördpinge eest.
- Transistorid: Kasutatakse voolu lülitamiseks ja signaalide võimendamiseks.
6.1.3 Näited alalisvoolu vooluringidest
Näide 1: Lihtne LED-vooluring
Komponendid:
- Patarei: 9 V
- Lüliti
- Takisti: 470 Ω (oomi)
- LED-lamp
- Juhtmed
Kirjeldus:
- Kui lüliti on suletud, voolab vool patareist läbi takisti ja LED-lambi, mis süttib.
- Takisti piirab voolu, et kaitsta LED-i liigse voolu eest.
- LED-lamp muundab elektrienergia valgusenergiaks.
Kujutis:
(Siin võiks olla skeem, mis näitab vooluringi ühendust.)
Näide 2: Mootori juhtimine lülitiga
Komponendid:
- Aku: 12 V
- Lüliti
- Elektrimootor
- Juhtmed
Kirjeldus:
- Lüliti sulgemisel voolab vool akust läbi elektrimootori, mis hakkab pöörlema.
- Elektrimootor muundab elektrienergia mehaaniliseks energiaks.
- Seda põhimõtet kasutatakse näiteks mänguautodes või ventilaatorites.
Näide 3: Päikesepaneeliga toitev süsteem
Komponendid:
- Päikesepaneel
- Laadimisregulaator
- Aku
- Alalisvoolu koormus: LED-valgustid, DC-pumbad
- Juhtmed
Kirjeldus:
- Päikesepaneel toodab alalisvoolu päikeseenergia muundamisel.
- Laadimisregulaator kontrollib aku laadimist, vältides ülelaadimist.
- Aku salvestab energiat, võimaldades süsteemil töötada ka pimedal ajal.
- Alalisvoolu koormused kasutavad salvestatud energiat töö tegemiseks.
Näide 4: Arduino mikrokontrolleri vooluring
Komponendid:
- USB-toide: 5 V alalisvool
- Arduino plaat
- Andurid ja aktuaatorid: Nupud, LED-id, servomootorid
- Juhtmed ja prototüüpimisplaat
Kirjeldus:
- Arduino saab toidet USB kaudu või alalisvoolu adapterist.
- Andurid (näiteks temperatuurisensorid) saadavad signaale Arduino plaadile.
- Aktuaatorid (näiteks mootorid, LED-id) juhitakse Arduino kaudu, mis kontrollib vooluringi vastavalt programmile.
6.1.4 Alalisvoolu eelised ja puudused võrreldes vahelduvvooluga
Eelised:
- Stabiilne ja ühtlane pinge:
- Sobib tundlike elektroonikaseadmete jaoks, mis vajavad konstantset voolu.
- Akude ja patareide kasutamine:
- Võimaldab kaasaskantavust ja sõltumatust võrgutoitest.
- Lihtsus elektroonikakomponentidega:
- Paljud elektroonikakomponendid töötavad paremini või ainult alalisvooluga.
- Ohutus madalatel pingetel:
- Madal pinge ja vool muudavad alalisvoolu ohutumaks teatud rakendustes.
Puudused:
- Energiakadu pikkadel vahemaadel:
- Suuremad energiakaod võrreldes vahelduvvooluga, mis teeb alalisvoolu ebaefektiivseks elektrienergia ülekandmisel suurtele vahemaadele.
- Pinge muundamise raskused:
- Alalisvoolu pinget on keerulisem tõsta või langetada ilma spetsiaalsete muunduriteta, kuna trafod ei tööta alalisvooluga.
- Piiratud ühilduvus võrguga:
- Enamus elektrivõrke kasutavad vahelduvvoolu, mistõttu alalisvooluseadmed vajavad adaptereid või muundureid.
- Kõrgemad kulud ülekandesüsteemides:
- Alalisvoolu ülekandesüsteemid võivad olla kulukamad ja keerulisemad rakendada.
6.1.5 Kokkuvõte
Alalisvool on oluline elektrivoolu tüüp, mida kasutatakse laialdaselt elektroonikas, sõidukites, taastuvenergia süsteemides ja paljudes muudes rakendustes. Selle stabiilsus ja ühtlus teevad selle ideaalseks tundlike seadmete jaoks, kuid samas on sellel piirangud elektrienergia edastamisel ja muundamisel. Mõistmine, kuidas alalisvoolu ahelad töötavad, ning nende eeliseid ja puudusi võrreldes vahelduvvooluga, on kriitiline elektrotehnika ja elektroonika valdkonnas.
Märkus: Lisatud on põhjalik ülevaade alalisvoolu põhimõtetest, rakendustest, vooluringi komponentidest ning toodud on mitmeid näiteid. Samuti on esitatud eelised ja puudused võrreldes vahelduvvooluga, nagu soovitud.
6.2 Vahelduvvoolu (AC) põhimõtted
Vahelduvvool (AC – Alternating Current) on elektrivool, mille suund ja tugevus muutuvad ajas perioodiliselt. Vahelduvvoolu puhul liiguvad elektronid edasi-tagasi, mitte ainult ühes suunas nagu alalisvoolu puhul. Tavaliselt on vahelduvvoolu kuju sinusoidaalne, mis tähendab, et pinge ja vool vahelduvad positiivsete ja negatiivsete väärtuste vahel teatud sagedusega.
Vahelduvvoolu peamised omadused:
- Sagedus: Sagedus näitab, mitu korda vool muudab suunda ühes sekundis. Vahelduvvoolu sagedus mõõdetakse hertsides (Hz).
- Euroopas on tavaliseks sageduseks 50 Hz, samas kui Põhja-Ameerikas on sagedus 60 Hz.
- Periood: Vahelduvvoolu täielik tsükkel koosneb ühest positiivsest ja ühest negatiivsest poolest. Periood (T) on ajavahemik, mille jooksul vool läbib ühe täistsükli.
![Rendered by QuickLaTeX.com \[T = \frac{1}{f}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-547a9baf00ff841aabb5ec2f33bbe856_l3.png)
kus: - T on periood (sekundites),
- f on sagedus hertsides (Hz).
- Efektiivväärtus (RMS): Kuna vahelduvvoolu pinge ja vool muutuvad ajas, kasutatakse praktikas efektiivväärtust (RMS – Root Mean Square), mis esindab sama võimsust kui alalisvoolu pinge või vool. Vahelduvvoolu pinge ja voolu RMS-väärtusi saab arvutada järgmiste valemitega:
![Rendered by QuickLaTeX.com \[U_{\text{RMS}} = \frac{U_{\text{max}}}{\sqrt{2}}, \quad I_{\text{RMS}} = \frac{I_{\text{max}}}{\sqrt{2}}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-2816ea09af1ea8efa31ffdfeb308bbef_l3.png)
kus: 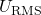 ja
ja 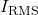 on vahelduvvoolu efektiivväärtused,
on vahelduvvoolu efektiivväärtused,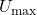 ja
ja 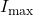 on vahelduvvoolu maksimaalsed väärtused.
on vahelduvvoolu maksimaalsed väärtused.
Vahelduvvoolu allikad:
- Generaatorid: Elektrijaamades toodetakse vahelduvvool generaatorite abil, kus mehaaniline energia muudetakse elektrienergiaks läbi magnetvälja ja pöörleva mehaanika.
- Inverterid: Inverterid muundavad alalisvoolu (nt päikesepaneelide toodetud energia) vahelduvvooluks, mida saab kasutada majapidamises või elektrivõrku tagasijuhituna.
6.2.1 Vahelduvvoolu faas ja faasinihe
Vahelduvvoolu (AC) analüüsimisel on faas ja faasinihe olulised mõisted, mis kirjeldavad pinge ja voolu suhet ajas. Vahelduvvoolus muutuvad nii pinge kui ka vool pidevalt ajas ja neil võib olla erinev faas ehk ajavahe, mille jooksul need saavutavad maksimaalse väärtuse.
6.2.2 Vahelduvvoolu faasi mõiste
Vahelduvvoolu puhul kirjeldab faas, millises punktis oma ajatsüklis (sinusoidses lainekujus) on pinge või vool igal ajahetkel. Faasi mõõdetakse kraadides või radiaanides, kus üks täistsükkel on 360 kraadi või ![]() radiaani. Tavaliselt kasutatakse pinge ja voolu faasi nihke analüüsimiseks sinusoidaalset lainekuju.
radiaani. Tavaliselt kasutatakse pinge ja voolu faasi nihke analüüsimiseks sinusoidaalset lainekuju.

- Sinusoidaalne pinge:
![Rendered by QuickLaTeX.com \[u(t) = U_{\text{max}} \cdot \sin(\omega t + \phi_u)\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-46202471685ee0744f6e89461497b8e1_l3.png)
kus: 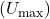 on pinge maksimaalne väärtus,
on pinge maksimaalne väärtus,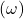 on nurksagedus
on nurksagedus 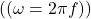 ,
,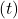 on aeg,
on aeg,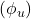 on pinge faasinurk.
on pinge faasinurk.- Sinusoidaalne vool:
![Rendered by QuickLaTeX.com \[i(t) = I_{\text{max}} \cdot \sin(\omega t + \phi_i)\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-a7deda5e7cfa653ab6f4aafed815b814_l3.png)
kus: 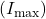 on voolu maksimaalne väärtus,
on voolu maksimaalne väärtus,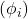 on voolu faasinurk.
on voolu faasinurk.
Faasinihe on erinevus pinge ja voolu faasinurkade vahel. See määrab, kas pinge ja vool on sünkroonis või kas üks neist “juhib” või “jääb maha” teise suhtes.
6.2.3 Faasinihe
Faasinihe ![]() on pinge ja voolu faaside vaheline erinevus. Kui pinge ja vool ei saavuta oma maksimaalseid väärtusi samal ajal, siis on nende vahel faasinihe. Faasinihet mõõdetakse kraadides või radiaanides.
on pinge ja voolu faaside vaheline erinevus. Kui pinge ja vool ei saavuta oma maksimaalseid väärtusi samal ajal, siis on nende vahel faasinihe. Faasinihet mõõdetakse kraadides või radiaanides.
- Kui pinge ja vool on täpselt ühes faasis (st faasinihe on 0), siis pinge ja vool on sünkroonis ja muutuvad ajas samal ajal.
- Kui pinge ja voolu vahel on faasinihe, siis üks saavutab maksimaalse väärtuse enne teist.
Faasinihe määratakse valemiga:
![]()
- Kui
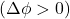 , siis pinge juhib voolu.
, siis pinge juhib voolu. - Kui
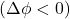 , siis vool juhib pinget.
, siis vool juhib pinget.
6.2.4 Faasinihe takisti, kondensaatori ja induktiivpooli korral
Elektrivooluringides võib faasinihe tekkida vastavalt sellele, millised komponendid vooluringis asuvad.
- Takisti (R) puhul ei ole faasinihet: pinge ja vool on sünkroonis, mis tähendab, et faasinihe on 0 kraadi.
- Kondensaatori (C) puhul jääb vool pingest 90 kraadi ette (vool juhib pinget).
- Induktiivpooli (L) puhul jääb vool pingest 90 kraadi maha (pinge juhib voolu).
Faasinihe takisti korral:
Takistiga vooluringis on pinge ja vool alati sünkroonis, kuna takisti ei põhjusta energiasalvestamist, vaid ainult energiakadu (soojusena).
Pinge ja vool takisti korral:
![]()
![]()
Faasinihe ![]() .
.
Faasinihe induktiivpooli korral:
Induktiivpool salvestab energiat magnetväljas, mille tõttu vool jääb pingest maha 90 kraadi võrra.
Pinge ja vool induktiivpooli korral:
![]()
![]()
Faasinihe ![]() (vool jääb maha pingest).
(vool jääb maha pingest).
Faasinihe kondensaatori korral:
Kondensaator salvestab energiat elektriväljas, mis tähendab, et vool juhib pinget 90 kraadi võrra.
Pinge ja vool kondensaatori korral:
![]()
![]()
Faasinihe ![]() (vool juhib pinget).
(vool juhib pinget).
6.2.5 Kompleksne impedants ja faasinihe
Vahelduvvoolu ahelate faasinihet on mugav analüüsida, kasutades kompleksset impedantsi ![]() , mis hõlmab nii takistuslikku (reaalosa) kui ka reaktiivset (imaginaarosa) komponenti. Impedants määrab, kuidas komponent reageerib vahelduvvoolule.
, mis hõlmab nii takistuslikku (reaalosa) kui ka reaktiivset (imaginaarosa) komponenti. Impedants määrab, kuidas komponent reageerib vahelduvvoolule.
- Takisti impedants:
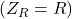
- Induktiivpooli impedants:
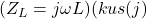 on imaginaarühik,
on imaginaarühik, 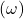 on nurksagedus ja
on nurksagedus ja 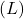 on induktiivsus)
on induktiivsus) - Kondensaatori impedants:
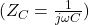
Impedants on komplekshulk, kus faasinihe on määratud reaktiivse ja takistusliku komponendi suhtega.
6.2.6 Näidisülesanne: Faasinihe induktiivpooliga vooluringis
Ülesanne:
Antud on vooluring, kus on vahelduvvoolu allikas sagedusega ![]() ja induktiivpool
ja induktiivpool ![]() . Arvutage faasinihe ja pinge ja voolu suhe.
. Arvutage faasinihe ja pinge ja voolu suhe.
Lahendus:
- Nurksagedus:
![Rendered by QuickLaTeX.com \[\omega = 2\pi f = 2\pi \times 50 \, \text{Hz} = 314.16 \, \text{rad/s}\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-72cf1e0b5e145923fae7fa7779b95d67_l3.png)
- Impedants induktiivpooli jaoks:
![Rendered by QuickLaTeX.com \[Z_L = j\omega L = j \times 314.16 \times 50 \times 10^{-3} = j15.71 \, \Omega\]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-01c0424845af93c1f1f84a72cb201cf3_l3.png)
- Faasinihe:
Induktiivpooli korral on faasinihe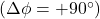 , mis tähendab, et vool jääb pingest maha.
, mis tähendab, et vool jääb pingest maha.
Graafiline illustratsioon (joonised)
- Faasinihke illustreerimiseks sinusoidaalsete lainekujude graafik:
- Graafik, mis näitab pinge ja voolu sinusoidaalseid laineid samal ajateljel, kus pinge ja vool on sünkroonis takisti korral, ning pinge juhib voolu induktiivpooli korral või vool juhib pinget kondensaatori korral.
- Takisti korral: pinge ja voolu lained kattuvad.
- Induktiivpooli korral: pinge laine saavutab maksimumi enne voolu lainet (90 kraadi faasinihe).
- Kondensaatori korral: voolu laine saavutab maksimumi enne pinge lainet (90 kraadi faasinihe vastupidises suunas).
Kokkuvõte:
Faas ja faasinihe on olulised mõisted vahelduvvooluahelate analüüsil, määrates pinge ja voolu omavahelise ajavahe. Faasinihe sõltub vooluringis olevatest komponentidest: takistid ei põhjusta faasinihet, samas kui induktiivpoolid põhjustavad voolu mahajäämist ja kondensaatorid põhjustavad voolu edasijõudmist pinge suhtes. Faasinihe on kriitiline arusaam elektriliste ahelate analüüsimisel, eriti kui kasutusel on reaktiivkomponendid, nagu induktiivpool
6.2.7 Vahelduvvoolu rakendused
Vahelduvvoolu kasutatakse laialdaselt, eriti elektrivõrkudes ja koduste elektrisüsteemide toiteks. AC on standardne elektrivoolu tüüp, mida kasutatakse enamikus maailma elektrivõrkudes ja seadmetes.
- Elektrienergia ülekandmine: Suurte vahemaade taha elektrienergia ülekandmine toimub vahelduvvooluga, sest pinge saab trafode abil tõsta ja langetada, vähendades energiakadu.
- Kodused elektrisüsteemid: Kõik pistikupesad ja enamik kodumasinaid (nt külmikud, telerid, valgustid) töötavad vahelduvvooluga.
- Suure võimsusega seadmed: Elektrimootorid, kliimaseadmed ja tööstuslikud seadmed kasutavad vahelduvvoolu, kuna see võimaldab efektiivselt edastada suurt võimsust.
- Trafo süsteemid: Trafod võimaldavad AC pinget tõsta või langetada vastavalt vajadusele, mida kasutatakse laialdaselt elektrijaamades ja kodustes elektrivõrkudes.
6.2.8 Vahelduvvoolu vooluringi komponendid
Vahelduvvoolu vooluringid koosnevad paljudest samadest komponentidest, mis on ka alalisvoolu vooluringides, kuid nende tööpõhimõtted ja kasutusviisid on mõnevõrra erinevad.
- Toiteallikas:
- Elektrijaamad ja generaatorid: Toidavad võrgusüsteeme suure võimsusega vahelduvvooluga.
- Inverterid: Muundavad alalisvoolu (nt akudest või päikesepaneelidest) vahelduvvooluks.
- Juhtmed:
- Elektrit juhtivad materjalid ühendavad vooluringi komponente ja võimaldavad voolu liikumist. Vahelduvvoolu puhul voolab vool pidevalt edasi-tagasi.
- Takistid (Resistorid):
- Takistid piiravad vahelduvvoolu voolutugevust ja jagavad pinget.
- Vahelduvvoolu takistus võib olenevalt sagedusest varieeruda, eriti kui kasutusel on induktiivpoolid või kondensaatorid.
- Kondensaatorid ja induktiivpoolid:
- Kondensaatorid salvestavad energiat elektriväljas ja lasevad läbi vahelduvvoolu kõrgsageduskomponendid, samal ajal blokeerides alalisvoolu.
- Induktiivpoolid (spiraalid) loovad magnetvälja ja takistavad vahelduvvoolu läbimist, eriti kõrgetel sagedustel.
- Trafod:
- Trafod on seadmed, mis kasutavad vahelduvvoolu, et tõsta või langetada pinge. Trafo tööpõhimõte põhineb elektromagnetilise induktsiooni seadusel.
6.2.9 Näited vahelduvvoolu vooluringidest
Näide 1: Lihtne vahelduvvoolu koduvalgustuse vooluring
Komponendid:
- Toiteallikas: Elektrivõrk (230 V, 50 Hz)
- Lüliti
- Lamp (koormus)
- Juhtmed
Kirjeldus:
- Kui lüliti on suletud, voolab elektrivõrgust vahelduvvool läbi lambi, mis süttib. Lamp kasutab vahelduvvoolu valgusenergia tootmiseks.
- Lüliti avamisel katkeb vooluring ja lamp kustub.
Näide 2: Trafo kasutamine pinge muutmiseks
Komponendid:
- Toiteallikas: Elektrivõrk (230 V, 50 Hz)
- Trafo: 230 V / 12 V
- Koormus: 12 V valgusdiood (LED)
- Juhtmed
Kirjeldus:
- Vahelduvvoolu allikas (elektrivõrk) annab kõrge pinge (230 V).
- Trafo muundab kõrge vahelduvvoolu pinge (230 V) madalaks vahelduvvooluks (12 V), et toita madalpingeseadmeid, näiteks LED-lampe.
6.2.10 Vahelduvvoolu võimsus (AC)
Vahelduvvoolu korral muutuvad pinge ja vool aja jooksul, seetõttu tuleb võimsust arvutada veidi erinevalt. Vahelduvvoolu korral on kaks peamist võimsuse tüüpi:
- Tegelik võimsus (aktiivne võimsus, P): See on võimsus, mis tehakse tegelikult kasulikuks tööks, näiteks soojuse või mehaanilise energia tootmiseks. Seda mõõdetakse vattides (W).
- Näiline võimsus (S): See on koguvõimsus, mis on saadud pinge ja voolu korrutisena ning mõõdetakse volt-amprites (VA).
- Reaktiivne võimsus (Q): See on võimsus, mis läheb edasi-tagasi energiasalvestusseadmete, näiteks kondensaatorite ja induktiivpoolide vahel. Seda mõõdetakse volt-amprites reaktiivses (VAR).
Valemid:
- Tegelik võimsus:
![Rendered by QuickLaTeX.com \[ P = U_{\text{eff}} \times I_{\text{eff}} \times \cos \phi \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-079ffed5e2714a398d666535701fffc6_l3.png)
Kus:
- Ueff on efektiivpinge (voldis, V),
- Ieff on efektiivvool (amprites, A),
- cos φ on võimsustegur (tavaliselt väärtus vahemikus 0 kuni 1).
- Näiline võimsus:
![Rendered by QuickLaTeX.com \[ S = U_{\text{eff}} \times I_{\text{eff}} \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-2fa1557c7710b2a7155b64dab1d8e42c_l3.png)
Seda mõõdetakse VA-s (volt-amprites). - Reaktiivne võimsus:
![Rendered by QuickLaTeX.com \[ Q = U_{\text{eff}} \times I_{\text{eff}} \times \sin \phi \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-36b6e291c8473e8560abe51bd7cc6e03_l3.png)
Seda mõõdetakse VAR-ides (volt-amprites reaktiivses).
Näide:
Oletame, et vahelduvvooluahelas on efektiivpinge 230 V, efektiivvool 5 A ja võimsustegur 0,8.
- Tegelik võimsus:
![Rendered by QuickLaTeX.com \[ P = 230 V \times 5 A \times 0,8 = 920 W \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-060d5d67ae40c03da57ffaf6c0085035_l3.png)
- Näiline võimsus:
![Rendered by QuickLaTeX.com \[ S = 230 V \times 5 A = 1150 VA \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-bc70af94d1d2972eab7a3d3b2e4ccbbd_l3.png)
- Reaktiivne võimsus:
![Rendered by QuickLaTeX.com \[ Q = 230 V \times 5 A \times \sin(\arccos(0,8)) \approx 690 VAR \]](https://ikt.tthk.ee/wp-content/ql-cache/quicklatex.com-4fa814e215ec2e46821edbae4fecd35c_l3.png)
Kokkuvõte
- Alalisvoolus on võimsuse arvutamine lihtne, korrutades pinge vooluga: ( P = U \times I ).
- Vahelduvvoolus on võimsuse arvutamine keerulisem, kuna arvestada tuleb võimsustegurit ja erinevaid võimsuse liike (tegelik, näiline ja reaktiivne võimsus).
Need valemid ja näited võimaldavad teil arvutada võimsust nii alalis- kui ka vahelduvvooluahelates, mis on oluline erinevate elektriliste seadmete ja süsteemide analüüsimisel ning projekteerimisel.
6.2.11 Vahelduvvoolu eelised ja puudused võrreldes alalisvooluga
Eelised:
- Energia efektiivne edastamine:
- Vahelduvvoolu pinget saab hõlpsasti tõsta ja langetada trafode abil, mis võimaldab elektrienergiat edastada pikkade vahemaade taha väikeste kadudega.
- Lihtsam pinge muundamine:
- Trafod töötavad ainult vahelduvvooluga ja võimaldavad tõhusat pinge muundamist, mis on oluline elektrivõrkudes ja kodustes süsteemides.
- Suuremahuline elektrivõrk:
- Elektrivõrgud üle maailma kasutavad vahelduvvoolu, kuna see sobib paremini võimsate süsteemide ja seadmete toiteks, nagu elektrimootorid ja kodumasinad.
- Tööstuslikud rakendused:
- Suure võimsusega elektrimootorid ja masinad töötavad vahelduvvooluga, kuna see võimaldab suuremat efektiivsust ja lihtsamat juhtimist.
Puudused:
- Tundlikkus sagedusele:
- Vahelduvvoolu süsteemid võivad olla tundlikud sageduse kõikumistele, mis võivad põhjustada seadmete ebaefektiivset tööd või kahjustusi.
- Elektroonikaseadmed vajavad alalisvoolu:
- Paljud elektroonikaseadmed töötavad alalisvooluga, mistõttu vajavad need adaptereid või alaldusseadmeid, mis muundavad vahelduvvoolu alalisvooluks.
- Võib põhjustada rohkem elektromagnetilist häiret:
- Vahelduvvoolu põhjustatud muutuvad magnetväljad võivad tekitada rohkem elektromagnetilist häiret, mis võib mõjutada tundlikke elektroonikaseadmeid.
6.2.12 Kokkuvõte
Vahelduvvool on maailmas laialdaselt kasutatav elektrivoolu tüüp, mis võimaldab energiat tõhusalt edastada pikkade vahemaade taha ja varustada suurt hulka koduseid ja tööstuslikke seadmeid. Vahelduvvoolu efektiivväärtus, pinge muundamise võimalus ja kasutusvõimalused suureskaalalistes elektrisüsteemides annavad sellele olulised eelised võrreldes alalisvooluga, kuigi elektroonikaseadmed nõuavad alalisvoolu, mistõttu on vajalik vahelduvvoolu muundamine alalisvooluks vastavate seadmete abil.
Märkus: Lisatud on vahelduvvoolu põhimõtted, rakendused, vooluringi komponendid ning arvutused, sealhulgas valemid ja näited. Samuti on välja toodud eelised ja puudused võrreldes alalisvooluga.
7. Pooljuhtseadised ja elektroonika põhialused
Pooljuhttehnoloogia on elektroonika süda, mis võimaldab luua erinevaid elektroonikaseadmeid, alates lihtsatest dioodidest ja transistoritest kuni keerukate integraallülitusteni. Selles peatükis käsitleme pooljuhtide põhimõtteid ja tüüpe, samuti dioodide ja transistorite tööpõhimõtteid ning rakendusi.
7.1 Pooljuhid
Põhimõtted:
Pooljuht on materjal, millel on elektrijuhtivus omadustes kuskil isolaatori ja juhi vahel. Pooljuhi juhtivust saab muuta, muutes temperatuuri, rakendades elektrivälja või lisades spetsiaalseid lisandeid (dopinguprotsess). Kõige levinumad pooljuhtmaterjalid on räni (Si) ja germaanium (Ge).
Tüübid: n- ja p-tüüpi pooljuhid
- n-tüüpi pooljuht:
- Põhimõte: n-tüüpi pooljuhis lisatakse pooljuhile viienda rühma elemente (näiteks fosforit), mille aatomitel on üks elektron rohkem kui räniaatomil. See lisaelektron ei ole tihedalt seotud aatomituumaga, mistõttu saab see hõlpsasti liikuda, tekitades elektrivoolu.
- Doping: Protsessi, mille käigus lisatakse lisandeid, et suurendada vabu elektrone, nimetatakse n-dopinguks. Selle tulemusena muutub pooljuht n-tüüpi pooljuhtiks, kus peamised laengukandjad on negatiivselt laetud elektronid.
- p-tüüpi pooljuht:
- Põhimõte: p-tüüpi pooljuhis lisatakse pooljuhile kolmanda rühma elemente (näiteks boori), mille aatomitel on üks valentselektron vähem kui räniaatomil. See loob “auke” ehk positiivseid laengukandjaid, mis võivad elektroni liikumisel liikuda läbi pooljuhi.
- Doping: Protsessi, mille käigus lisatakse lisandeid, et luua aukude liikuvust, nimetatakse p-dopinguks. Selle tulemusena muutub pooljuht p-tüüpi pooljuhiks, kus peamised laengukandjad on positiivsed augud.
Dopinguprotsess:
Dopinguprotsess seisneb lisandite lisamises puhtale pooljuhtmaterjalile, et muuta selle elektrilisi omadusi. See protsess võimaldab kontrollida pooljuhi juhtivust, luues n- või p-tüüpi pooljuhte. n- ja p-tüüpi pooljuhte kombineerides saab luua erinevaid elektroonilisi komponente, nagu dioodid ja transistorid.
7.2 Dioodid ja transistorid
Dioodid
Tööpõhimõte:
Diood on kahepoolne pooljuhtseadis, mis koosneb n- ja p-tüüpi pooljuhtidest, mis on ühendatud p-n ühenduseks. Diood lubab elektrivoolu voolata ainult ühes suunas – p-tüüpi pooljuhist n-tüüpi pooljuhti. Kui p-tüüpi pooljuhile (anoodile) rakendatakse positiivne pinge ja n-tüüpi pooljuhile (katoodile) negatiivne pinge, avatakse diood ja vool saab voolata. Kui pinge suund on vastupidine, blokeerib diood voolu.
Tüübid:
- Tavaline diood: Kasutatakse voolu suuna juhtimiseks ja pinge stabiliseerimiseks.
- Zeneri diood: Mõeldud töötama vastupidises suunas, võimaldades stabiliseerida pinge kindlal väärtusel.
- LED (valgusdiood): Kiirgab valgust, kui selle kaudu voolab vool.
- Schottky diood: Madala pingelangusega diood, mis võimaldab kiiret lülitumist.
Rakendused:
- Alaldi vooluringides: Dioodid muundavad vahelduvvoolu alalisvooluks.
- Pingestabilisaatorid: Zeneri dioode kasutatakse pingetaseme stabiliseerimiseks.
- Valgusallikad: LED-e kasutatakse valgustus- ja signaalseadmetes.
- Kaitse vooluringides: Dioodid kaitsevad komponente liigse voolu ja pöördpolarisatsiooni eest.
Transistorid
Tööpõhimõte:
Transistor on pooljuhtseadis, mida kasutatakse signaalide võimendamiseks ja lülitamiseks. Transistor koosneb kolmest kihi pooljuhist, mis moodustavad kaks p-n üleminekut. Neid kihte tähistatakse järgmiselt:
- Bipolaarne transistori puhul on kaks tüüpi: NPN ja PNP.
- NPN transistori puhul on kaks n-tüüpi pooljuhti eraldatud p-tüüpi pooljuhtkihiga.
- PNP transistori puhul on kaks p-tüüpi pooljuhti eraldatud n-tüüpi pooljuhtkihiga.
Transistoril on kolm terminali:
- Kollektor (C): Kollektorile kogutakse vool.
- Emiter (E): Emitrist väljub vool.
- Baasklemm (B): Baasklemmi kaudu juhitakse transistori tööd.
Kui baasvool rakendatakse baasklemmi ja emitteri vahel, võimaldab see suuremat voolu voolata kollektorist emitterisse. Seda omadust kasutatakse signaalide võimendamiseks ja lülitite loomiseks.
Tüübid:
- Bipolaarne transistori (BJT): Kasutatakse võimendites ja lülitites.
- Väljatransistori (FET): Kasutatakse kõrge impedantsiga rakendustes, näiteks digitaalsetes vooluringides.
- MOSFET: Kasutatakse energiatõhusates ja kiiretes lülitustes, näiteks mikroprotsessorites ja toiteallikates.
Rakendused:
- Võimendid: Transistorid võimendavad helisignaale raadiotes ja helivõimendites.
- Lülitid: Transistorid toimivad lülititena arvutite loogikalülitustes ja toiteallikates.
- Digitaalsed vooluringid: MOSFETid on kasutusel arvutikiipides ja mälu moodulites.
- Võimendusvõimendid: Transistorid kasutatakse väikeste signaalide võimendamiseks telekommunikatsiooni seadmetes.
Pooljuhtide ja pooljuhtseadiste tundmine on elektroonika aluste oluline osa. Pooljuhid, nagu dioodid ja transistorid, on kaasaegsete elektrooniliste seadmete ehituskivid, võimaldades signaalide juhtimist, võimendamist ja töötlemist. Nende seadiste põhimõtete ja tööprotsesside mõistmine on vajalik elektroonika valdkonna edasiõppimiseks ja praktiliste rakenduste arendamiseks.
8. Digitaalelektroonika põhialused
Digitaalelektroonika tegeleb signaalide ja informatsiooni töötlemisega kahendsüsteemi abil, kus kasutatakse kahte põhiväärtust: 0 ja 1. Need väärtused esindavad loogilisi seisundeid ja on aluseks loogikalülitustele ja binaararvutustele, mis moodustavad tänapäevase arvutitehnika ja digitaalelektroonika aluse.
8.1 Loogikalülitused
Loogikalülitused on elektroonilised komponendid või vooluringid, mis töötlevad kahendsüsteemi väärtusi vastavalt teatud loogilistele reeglitele. Peamised loogikalülitused on AND, OR ja NOT lülitused.
1. AND lülitus (JA-lülitus):
- Põhimõte: AND-lülitus annab väljundiks 1 ainult siis, kui kõik sisendid on 1. Kui üks või mitu sisendit on 0, on väljund 0.
- Sümbol:

- Tõeväärtustabel:
| Sisend A | Sisend B | Väljund (A AND B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. OR lülitus (VÕI-lülitus):
- Põhimõte: OR-lülitus annab väljundiks 1, kui vähemalt üks sisenditest on 1. Väljund on 0 ainult siis, kui kõik sisendid on 0.
- Sümbol:

- Tõeväärtustabel:
| Sisend A | Sisend B | Väljund (A OR B) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
3. NOT lülitus (EI-lülitus):
- Põhimõte: NOT-lülitus (inverter) muudab sisendi väärtuse vastupidiseks. Kui sisend on 1, on väljund 0 ja vastupidi.
- Sümbol:

- Tõeväärtustabel:
| Sisend | Väljund (NOT A) |
|---|---|
| 0 | 1 |
| 1 | 0 |
Rakendused:
- Loogikalülitused on aluseks digitaalsetele vooluringidele ja arvutite loogikalülitustele, nagu protsessorid ja mälu. Neid kasutatakse otsuste tegemiseks (nt võrreldes kahendsüsteemi väärtusi) ja erinevate funktsioonide (nt liitmine, lahutamine) teostamiseks digitaalsüsteemides.
8.2 Binaararvutused ja -tehted
Binaararvutused kasutavad kahendsüsteemi (binaarsüsteemi), kus iga number esitatakse ainult kahes olekus: 0 või 1. Binaarsüsteem on arvutite ja digitaalelektroonika aluseks, kuna see võimaldab andmete tõhusat salvestamist ja töötlemist.
Binaarsüsteemi olemus:
- Kahendsüsteem: Binaarsüsteem kasutab kahte sümbolit, 0 ja 1, ning põhineb kahekümnendikorrutustel (2^n). Iga positsioon binaararvus esindab vastavat kahekümnendikorrutist.
- Näide: Binaararv 1101 on kümnendsüsteemis võrdne 13-ga:
- (1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) = 8 + 4 + 0 + 1 = 13
Binaarliitmine:
Binaarliitmine toimub sarnaselt kümnendsüsteemi liitmisele, kuid kahes olekus (0 ja 1). Kaks binaararvu liidetakse järgmiselt:
| Bitid | Arvutus | Väljund |
|---|---|---|
| 0 + 0 | 0 | 0 |
| 0 + 1 | 1 | 1 |
| 1 + 0 | 1 | 1 |
| 1 + 1 | 10 (1) | 0, ülekandega 1 järgmisesse kohta |
Näide:
Lisame kaks binaararvu 1011 ja 1101:
1011- 1101
11000
Siin on ülekande kohta tulemuseks viies koht (1), mistõttu saame tulemuseks 11000.
Binaarlahutamine:
Binaarlahutamine on samuti sarnane kümnendsüsteemi lahutamisele, kuid see toimub kahes olekus. Kui tuleb lahutada suuremast numbrist väiksem arv, laenatakse ülemisest kohast.
| Bitid | Arvutus | Väljund |
|---|---|---|
| 0 – 0 | 0 | 0 |
| 1 – 0 | 1 | 1 |
| 1 – 1 | 0 | 0 |
| 0 – 1 | 10 – 1 | 1, laenuga 1 järgmisse kohta |
Näide:
Lahutame binaararvud 1101 ja 1010:
1101- 1010
0011Rakendused:
- Binaararvutused on aluseks arvutite matemaatilistele operatsioonidele, sealhulgas liitmisele, lahutamisele, korrutamisele ja jagamisele. Kõik andmetöötlus arvutis toimub binaarsüsteemi põhjal.
- Binaarsüsteem võimaldab esitada andmeid, näiteks teksti, pilte ja heli, digitaalsetes seadmetes, kasutades ainult kahte olekut.
Digitaalelektroonika põhialused hõlmavad loogikalülituste ja binaararvutuste mõistmist. Loogikalülitused võimaldavad andmete töötlemist ja otsuste tegemist, samas kui binaarsüsteem moodustab arvutustehnika ja andmetöötluse aluse. Nende kontseptsioonide mõistmine on ülioluline, et mõista, kuidas tänapäevased digitaalseadmed töötavad ja kuidas nad töötlevad ja salvestavad teavet.














