KONTROLLER - Tööstuslikud infovõrgud ja IT turvalisus

PID kontroller

Kontrolleri ülesandeks automaatreguleerimise süsteemis on mõjutada protsessi niimoodi, et protsessi väärtus x vastaks seadesuurusele w. Kontroller koosneb võrdluselemendist ja võimendist (Joonis 4.1).

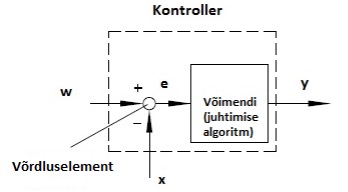
Joonis 4.1 Kontrolleri ehitus (Controllers and Controlled Systems, Samson AG,1999)

Võrdluselement kalkuleerib veasignaali e etteandesuuruse w ja protsessi muutuja x vahena. Võimendi genereerib veasignaalist e juhttoime signaali y.

Sõltuvalt kontrolleri väljundsignaali tüübist võib juhttoime olla pidev või katkeline (Joonis 4.2).

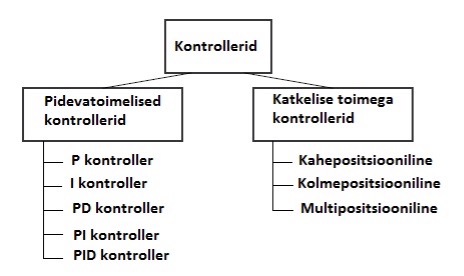
Joonis 4.2 Kontrollerite klassifitseerimine (Controllers and Controlled Systems, Samson AG,1999)

Pidevattoimelise kontrolleri väljundsignaal (juhttoime y) võib omada mistahes väärtust kontrolleri väljundsignaali diapasooni ulatuses. Pidevatoimelise kontrolleri tunnusjoon kujutab tavaliselt proportsionaalset (P), integraalset (I) või diferentsiaalset (D) toimet või nende toimete kombinatsiooni.

Katketoimelise kontrolleri väljundsignaal muutub diskreetsete suurustena. Tehakse vahet kahepositsiooniliste, kolmepositsiooniliste ja multipositsiooniliste kontrollerite vahel.

4.1 KATKELISE TOIMEGA KONTROLLERID

Pidevatoimelise kontrolleri väljundsuurus võib omada mistahes väärtust vahemikus y0 kuni ymax. Katkelise toimega kontrollerite väljundsignaalid omavad ainult teatud diskreetseid väärtusi.

4.1.1. KAHEPOSITSIOONILINE KONTROLLER

Lihtsaim katkelise toimega kontroller on kahepositsiooniline kontroller, mille väljund võib omada ainult kahte väärtust: 0 või ymax. Tüüpiliseks näiteks on elektrilise triikraua temperatuuri reguleerimine bimetallist lülituselemendi abil ( Joonis 4.3).

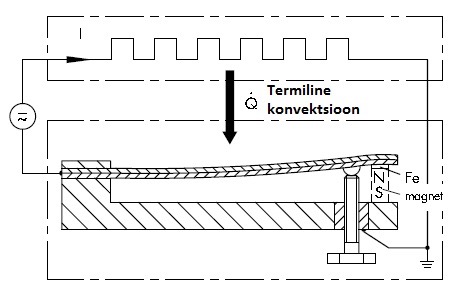
Joonis 4.3 Temperatuuri juhtimine bibetallist lüliti abil (Controllers and Controlled Systems, Samson AG,1999)

Bimetall on antud juhul nii mõõte- kui ka lülituselement. Kui lülitada triikraud sisse, siis toimub kuumutusplaadi soojendamine läbi bimetallist lüliti. Teatud temperatuuri juures paindub bimetallist lüliti ülemine metall rohkem kui alumine, mille tulemusel vooluahel katkeb. Temperatuuri alanedes sulgub kontakt uuesti.

Kahetoimelise kontrolleri lülituskarakteristik on toodud Joonisel 4.4.

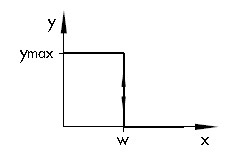
Joonis 4.4 Kahetoimelise kontrolleri lülituskarakteristik (Control technology,Siemens)

Ülaltoodud karakteristiku korral lülitub kontrolleri väljund y välja x = w juures. Juhul, kui tekib minimaalne kõrvalekalle seadesuurusest, lülitub y uuesti sisse. Sellise karakteristiku juures võib toimuda liiga sage väljundi ümberlülitumine, mis võib kahjustada kontrolleri väljundelementi. Selle vältimiseks muudetakse lülituskarakteristikut nii, et sisse- ja väljalülituse punktid viiakse üksteisest eemale X_sd võrra e. tekitatakse hüsterees (Joonis 4.5). Sellega väheneb ümberlülituste sagedus märgatavalt, kuid tekib protsessi väärtuse x perioodiline võnkumine hüstereesi laiuse ulatuses.

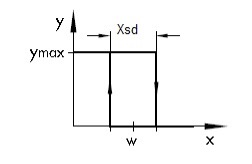
Joonis 4.5 Kahetoimelise kontrolleri hüstereesiga lülituskarakteristik (Control technology,Siemens)

Järgneval joonisel on kujutatud kütmise suletud ahelaga juhtimist (Joonis 4.6):

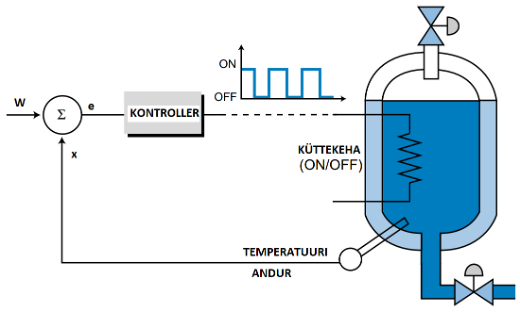
Joonis 4.6 Temperatuuri katkeline juhtimine

Tüüpiline esimest järku protsessi juhtiva kahetoimelise kontrolleri juhtimistsükli näide on toodud Joonisel 4.7.

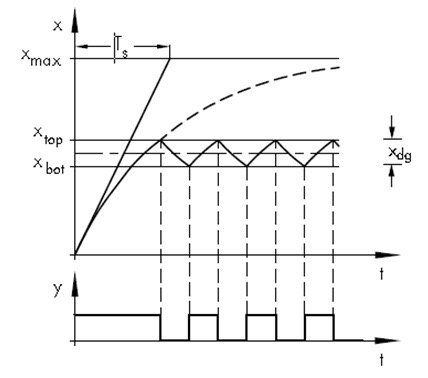
Joonis 4.7 Kahepositsioonilise kontrolleri juhtimistsükkel (Controllers and Controlled Systems, Samson AG,1999)

Lülitussagedus sõltub protsessi parameetrist Ts ja hüstereesi suurusest. Kui Ts väheneb, siis suureneb ümberlülituste sagedus. Seega lühikese ajakonstandiga protsesside reguleerimiseks ei ole kahepositsiooniline kontroller sobiv.

Kõrgemat järku protsesside korral tekib ülereguleerimine (Joonis 4.8). Seadesuuruse saavutamisel lülitub väljund ümber, kuid protsessi väärtus kasvab veel teatud suuruseni aja Tu jooksul. Sama toimub ka sisselülitamise punktis. Kahetoimelist kontrollerit kasutatakse lihtsate protsesside juhtimiseks, kus nõuded protsessi parameetri stabiilsusele on väikesed.

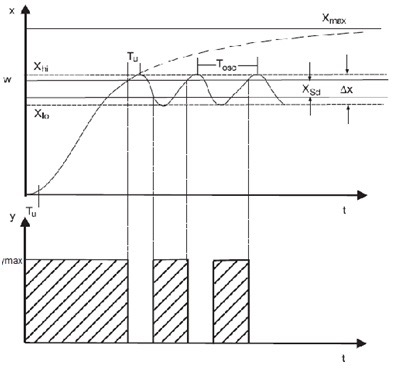
Joonis 4.8 Kahepositsiooniline kontroller kõrgemat järku protsessis (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)

Kahepositsiooniline juhtimine on odav kuid mitte piisavali täpne enamike tööstuslike protsesside jaoks. Enamasti kaasneb kahepositsioonilise reguleerimisega ülereguleerimine. Väljundparameeter võngub pidevalt seadesuuruse ümber.

4.1.2. KOLMEPOSITSIOONILINE KONTROLLER

Kahepositsioonilise kontrolleri puuduseks on see, et temaga ei ole võimalik juhtida reversiivseid protsesse või etapiviisilist lülitust. Kolmepositsiooniline kontroller on kombinatsioon kahest kahepositsioonilisest kontrollerist. Kolmepositsioonilisel kontrolleril on kolm väljundsignaali taset. Temperatuuri juhtimise süsteemis oleks väljundsignaalideks „küte sees”, „küte väljas” ja „jahutus sees” (Joonis 4.9).

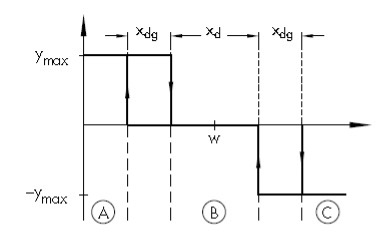
Joonis 4.9 Kolmepositsioonilise kontrolleri lülituskarakteristik (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)

Kolmepositsioonilise kontrolleri abil saab vähendada väljundsignaali võnkuvat käitumist, sest ta pakub lisaks „sees” või „väljas” signaalidele (kahepositsioonilise kontrolleri puhul) veel vahepealset väljundsignaali, mis asub väljundsignaali diapasooni keskpunktis (joonis 4.10).

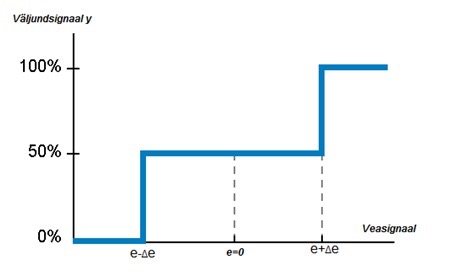
Joonis 4.10 Kolmeastmelise kontrolleri väljundsignaal (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)

Kui seadesuurus on saavutatud, siis kontrolleri väljundsignaal jääb 50% -liseks maksimaalsest väljundsignaalist ymax. Näitena vaatame temperatuuri reguleerimist seadesuurusega w = 50̊ C (joonis 4.11).

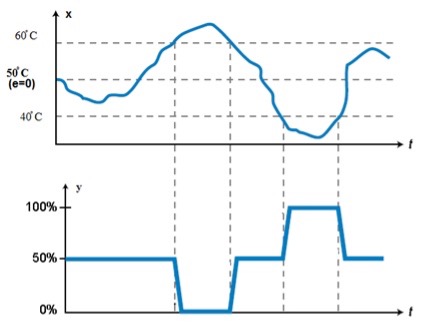
Joonis 4.11 Temperatuuri reguleerimine kolmeastmelise kontrolleriga (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)

Kui temperatuur jääb 40̊ C ja 60̊ C vahele, siis on kütteelement lülitatud sisse 50% -lise võimsusega. Temperatuuri tõustes üle 60̊ C lülitatakse küttevõimsus välja ning temperatuuri langemisel alla 40̊ C lülitatakse küte 100%-liselt sisse.

Multipositsioonilise kontrolleri puhul on väljundsignaalide tasemeid rohkem kui kolm (Joonis 4.12).

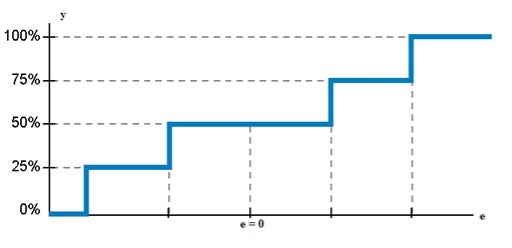
Joonis 4.12 Multipositsioonilise kontrolleri lülituskarakteristik (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)

Kolme ja enampositsioonilisi kontrollereid kohtab praktikas harva, sest pole eriti palju mitmepositsioonilise juhtimisega täiturelemente.

4.2 PIDEVATOIMELISED KONTROLLERID

Enamiku protsesside juhtimiseks kasutatakse pidevatoimelist kontrollerit. Pidevatoimeline kontroller saadab analoogsignaali täiturelemendile, millega mõjutatakse protsessi väärtust nii, et veasignaal muutub suletud ahelaga juhtimise korral nulliks.

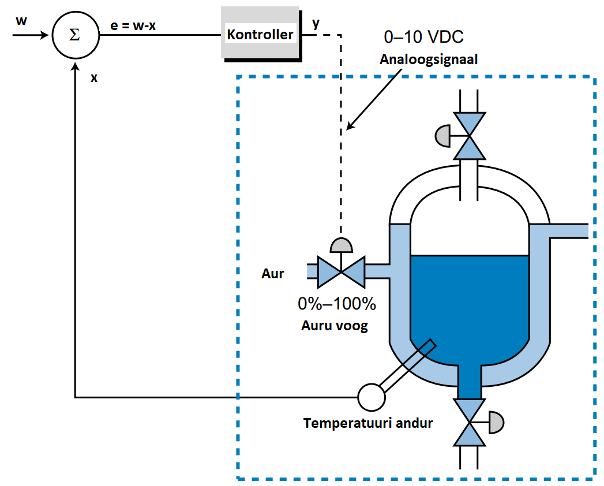
Joonis 4.13 Pidevatoimeline kontroller

4.2.1 P KONTROLLER

P kontrolleri väljundsignaal y ( protsessi juhttoime) on proportsionaalne (võrdeline) veasignaaliga e. P kontroller reageerib veasignaali e muutusele ilma viivituseta. P kontrolleri väljundsignaal tekib ainult veasignaali e olemasolul. Kui veasignaal puudub (st. protsessi muutuja väärtus on täpselt võrdne etteantud väärtusega w), siis p kontrolleri väljundsignaal puudub (on võrdne nulliga).

P kontrolleri dünaamiline karakteristik on kujutatud Joonisel 4.14.

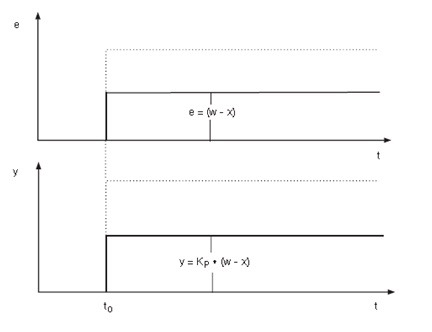
Joonis 4.14 P kontrolleri dünaamiline tunnusjoon (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)

P kontrolleri väljundsuurus y on määratud proportsionaalse toime koefitsendiga K_P:

y = K_P *e

See on lineaarne sõltuvus ( Joonis 4.15). Mida suurem on proportsionaalse toime koefitsendi K_P väärtus seda suurem on graafiku tõusunurk ja seega ka väljundsuurus y.

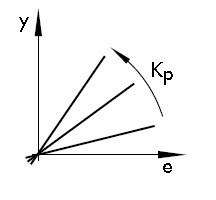
Joonis 4.15 Väljundsuuruse y sõltuvus koefitsendist K_P (Controllers and Controlled Systems, Samson AG,1999)

P kontrolleriga suletud juhtimisahelas tekib alati häiringute või seadesuuruse muutumise korral protsessi muutuja staatiline viga.

Kontroller püüab kompenseerida häiringust tingitud protsessi muutuja x muutumise genereerides juhttoime signaali, mis toimib häiringust toimunud x muutusele vastupidises suunas. Kuna P kontroller tekitab juhttoime ainult kõrvalekalde olemasolul, siis permanentset muutust, mida nimetatakse staatiliseks veaks, pole P kontroller võimeline kompenseerida (Joonis 4.16).

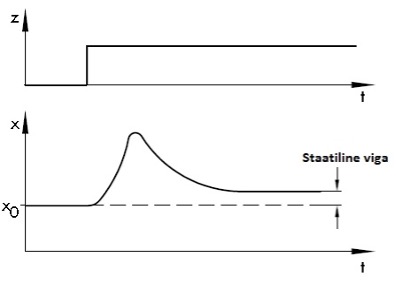
Joonis 4.16 Staatiline viga P kontrolleri korral (Controllers and Controlled Systems, Samson

AG,1999)

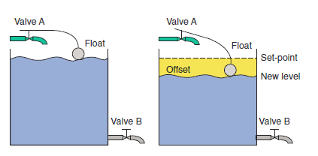
Joonis 4.17 Staatilise vea tekkimine häiringu korral.

Häiringu korral toimub järgmine protsess (Joonis 4.17):

kui ventiil B avaneb, hakkab vedelik mahutist välja voolama ja tema nivoo langeb;
vedeliku nivoo langemine toob kaasa ujuki madalamale laskumise, mis omakorda tekitab ventiili A avanemise ja vedeliku sissevoolamise paaki;
selline protsess kestab seni kuni ujuk on avanud ventiili A niivõrd, et vedeliku sissevool paaki võrdsustub vedeliku väljavooluga paagist;
staatilise vea tõttu stabiliseerub vedeliku tase uuel väärtusel, mis aga erineb etteandeväärtusest.

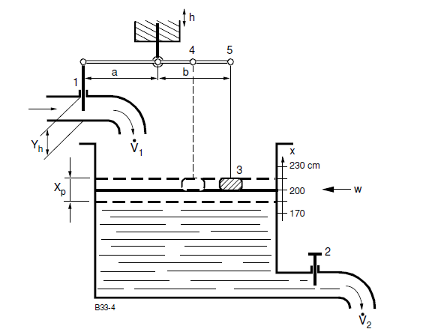
Joonis 4.18

Joonis 4.19

Staatilise vea suurus sõltub P kontrolleri koefitsiendist K_P. Mida suurem on K_P, seda väiksem on staatiline viga.

P kontrolleri tingmärk skeemidel:

P kontrollerid on kiiretoimelised. Neid võib kasutada seal, kus ei esitata väga rangeid nõudmisi reguleerimisprotsessile ja kus on lubatav staatilise vea tekkimine.

P kontrolleri kasutamise eelised:

– P kontroller on kiiretoimeline;

– õigesti valitud KP korral väga stabiilne reguleerimisprotsess.

P kontrolleri kasutamise puudused:

– häiringute toimel staatilise vea tekkimine.

4.2.2 I KONTROLLER

Integraalset kontrollerit kasutatakse selleks, et täielikult kõrvaldada kõrvalekalle mistahes reguleerimispunktis. Niikaua kui kõrvalekalle ei ole null, põhjustab integraalne toime juhttoime muutuse. Kontrolleri väljundsuurus muutub proportsionaalselt veasignaali integraalile (Joonis 4.20):

Kui kiiresti suureneb/väheneb juhttoime y, see sõltub vea suurusest ja integreerimise ajast Tn. Kui integreerimise aeg on lühike, siis kontrolleri väljundsignaal muutub kiiresti ja vastupidi.

Joonis 4.20 I kontrolleri dünaamiline karakteristik (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)

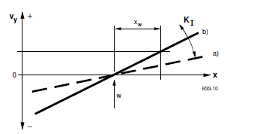
Joonis 4.21

Mida suurem on e ja mida suurem on Ki, seda suurem on kontrolleri väljundsignaal.

I kontrolleri puhul muutub sama suure veasignaali korral väljundsignaal y palju aeglasemalt kui P kontrolleri puhul. Kui lühendada integreerimise aega, siis y muutus kiireneb, kuid tekib süsteemi võnkumamineku oht.

I kontrolleri tingmärk skeemidel:

I kontrolleri kasutamise eelised:

– I kontroller ei jäta staatilist viga.

I kontrolleri kasutamise puudused:

– suure integreerimise aja korral väljundsignaali y muutus liiga loid;

– lühikese integreerimise aja korral süsteemi võnkumamineku oht (ebastabiilsus).

4.2.3 D KONTROLLER

D (diferentsiaalne ) kontroller genereerib juhttoime y lähtuvalt veasignaali muutumise kiirusest, mitte selle amplituudist. Järelikult D kontroller reageerib palju kiiremini kui P kontroller. Isegi siis, kui veasignaal on väike, genereerib D kontroller suure amplituudiga juhttoime juhul kui veasignaal muutub. Kui veasignaal on konstantne (sõltumata tema suurusest), siis on D kontrolleri väljundsignaal 0. D kontrollerit üksikuna kasutatakse väga harva. Tavaliselt kasutatakse teda koos teiste kontrolleritüüpidega, peamiselt koos P kotrolleriga.

Ideaalse D kontrolleri dünaamiline karakteristik veasignaali järsul muutumisel on toodud Joonisel 4.22.

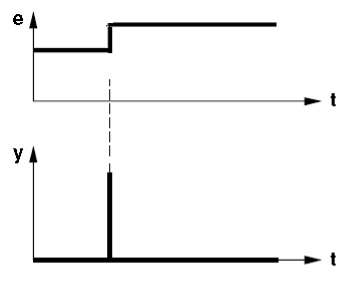
Joonis 4.22 Ideaalse D kontrolleri dünaamiline karakteristik (Control technology,Siemens)

Ideaalse D kontrolleri väljundis tekib veasignaali hüppelise muutumise korral lõpmatu amplituudiga väga lühiajaline impulss. Peale väljundsignaali y impulsi lõppu muutub väljundsignaal kohe nulliks, kuigi veasignaal jääb kestma.

D kontrolleri iseloomustamiseks sobib palju paremini ühtlaselt muutuva veasignaali muutuse karakteristik, mis näitab väljundsignaali y muutumist erinevate veasignaali muutumise kiiruste muutumise korral (Joonis 7.23).

D kontrolleri korral on väljundsignaali muutumise ulatus ΔyD proportsionaalne vea muutumise kiiruse muutumisega vx. D kontrollerit iseloomustab diferentsiaalse toime koefitsient KD, mis väljendab seost väljundsuuruse muutumise ulatuse ΔyD ja veasignaali kiiruse muutumise kiiruse vahel vx:

KD = ΔyD / vx

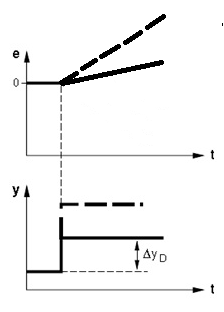
Joonis 4.23 D kontrolleri ühtlaselt muutuva veasignaali muutuse tunnusjoon (Control technology,Siemens)

D kontrolleri tingmärk:

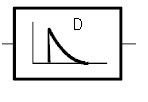
4.2.4 PI KONTROLLER

PI kontroller (Joonis 4.24) saadakse siis, kui ühendatakse paralleelselt P ja I kontrollerid. PI kontrolleri dünaamiline karakteristik on P kontrolleri ja I kontrolleri karakteristikute summa (Joonis 4.25).

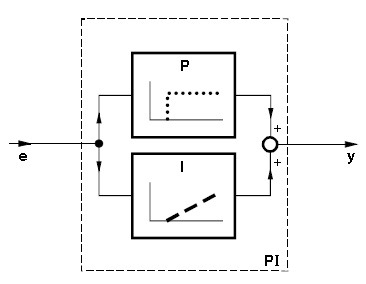
Joonis 4.24 PI kontroller (Control technology,Siemens)

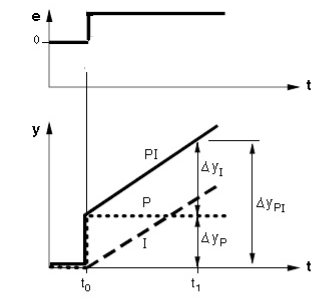
Joonis 4.25 PI kontrolleri dünaamiline karakteristik (Control technology,Siemens)

P kontroller tekitab esmase väljundsuuruse tõusu ΔyP, mis on võrdeline veasignaaliga e. I kontrolleri toime tõttu hakkab väljundsignaal y kasvama kiirusega, mille määrab ära integreerimise koefitsient KI. Teatud kindla aja möödumisel (t0…t1) koosneb väljundsignaali muutus ΔyPI kahe komponendi summast:

ΔyPI= ΔyP + ΔyI

Kui veasignaal e jääb kestma, siis jätkub väljundsignaali y tõus lõpmatult.

PI kontroller on määratud kahe reguleeritava parameetriga:

esimene karakteristik on P kontrolleri proportsionaalse toime koefitsient KP;
teiseks karakteristikuks on integraalse toime aeg Tn, mis tuleneb I kontrolleri tegurist KI.

Tn on aeg mida I kontroller vajab (sama sisendsignaali juures), et tekitada väljundsignaali muutus ΔyI, on mis võrdne P kontrolleri poolt tekitatud väljundsignaali muutusega ΔyP (Joonis 4.26).

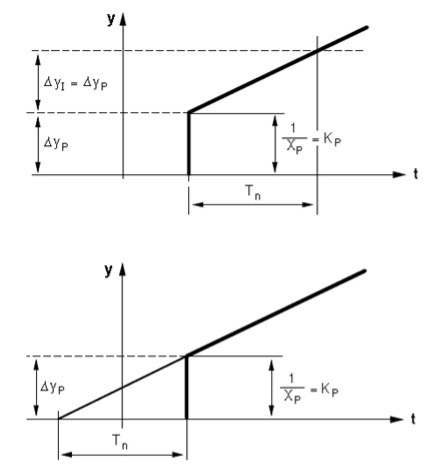
Joonis 4.26 Integraaltoime aja Tn definitsioon (Control technology,Siemens)

Puhtalt I kontroller peaks sama sisendsignaali korral aja Tn võrra varem hakkama avaldama toimet, et tekitada väljundsignaali muutus ΔyP, mille tekitab P kontroller.

4.2.5 PD KONTROLLER

PD kontrolleri moodustavad paralleelselt ühendatud P ja D kontroller (Joonis 4.27).

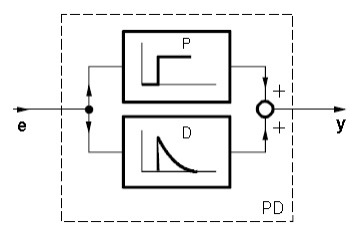
Joonis 4.27 PD kontroller (Control technology,Siemens)

PD kontrolleri dünaamiline karakteristik kujutab endast P kontrolleri ja D kontrolleri karakteristikute summat (Joonis 4.28).

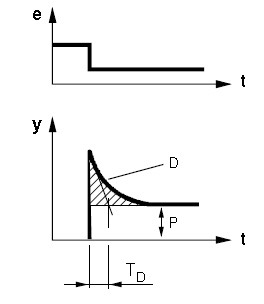
Joonis 4.28 PD kontrolleri dünaamiline karakteristik (Control technology,Siemens)

Tänu D toimele tekitab kontroller veasignaali e astmelisel muutumisel suure väljundsignaali y, mis hakkab ajakonstandiga TD eksponentsiaalselt vähenema kuni nullini. Edasi määrab kontrolleri toime P komponent. PD kontroller suudab veasignaali kompenseerida märksa kiiremini kui aimult P kontroller. Nii nagu P kontroller tekitab ka PD kontroller staatilise vea.

PD kontrolleri kirjeldamiseks sobib paremini ühtlaselt muutuva veasignaali muutuse tunnusjoon (Joonis 4.29).

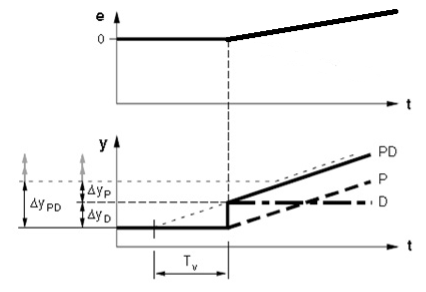
Joonis 4.29 PD kontrolleri ühtlaselt muutuva veasignaali muutuse tunnusjoon (Control technology, Siemens)

PD kontrollerit iseloomustavad järgmised suurused:

– P kontrolleri proportsionaalse toime koefitsient KP;

– D kontrolleri koefitsient KD või diferentsiaalse toime aeg Tv.

Diferentsiaalse toime aeg Tv näitab kui kaua enne tunnusjoone murdepunkti oleks pidanud algama P kontrolleri toime tõus , et saavutada väljundsignaali tõus ΔYD, mille D kontroller saavutab hetkeliselt.

4.2.6 PID KONTROLLER

PID kontroller kujutab endast P, I ja D kontrolleri paralleelühendust (Joonis 4.30).

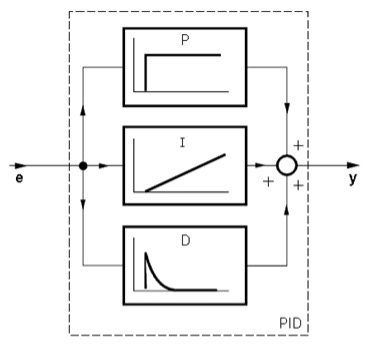
Joonis 4.30 PID kontroller (Control technology,Siemens)

PID kontrolleri dünaamiline tunnusjoon: (Joonis 4.31).

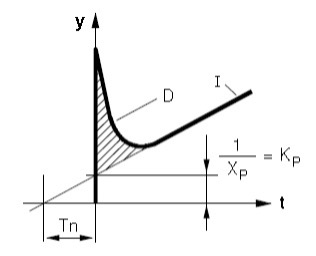
Joonis 4.31 PID kontrolleri tunnusjoon (Control technology,Siemens)

PID kontrolleri dünaamiline tunnusjoon kujutab P, I ja D elementide tunnusjoonte summat. Esialgne suur väljundsignaali y tõus on tingitud D elemendist, seejärel tunnusjoon langeb peaaegu P elemendi tunnusjoone tasemeni ja siis hakkab lineaarselt tõusma I elemendi tunnusjoone toimel. I elemendi tõttu kompenseerib PID kontroller seadesuuruse või häiringute poolt tekitatud veeasignaali muutused ja on kiirem kui PI või P kontroller.

PID kontrolleri dünaamiline tunnusjoon on määratud kolme parameetriga:

P kontrolleri proportsionaalse toime koefitsient KP;
integraalse toime aeg Tn;
diferentsiaalse toime aeg Tv.

PID kontrollerit kasutatakse keeruliste süsteemide korral, kus nõutakse kiiret stabiliseerumist ja staatilise vea olemasolu pole lubatud.

4.3 KVASI-PIDEV KONTROLLER

Kvasi-pidev kontroller koosneb pidevast kontrollerist, mille väljundisse on ühendatud lülituselement.

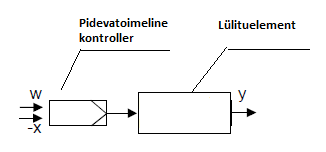
Joonis 4.32 Kvasi-pidev kontroller

Sellise kontrolleri väljundsignaal omab väärtusi 0% või 100% (kas sees või väljas). Sujuvalt muudetakse sees ja väljasoleku aegade suhet. Suhte sujuva muutmisega muudetakse sisuliselt väljundsignaali keskmist väärtust.

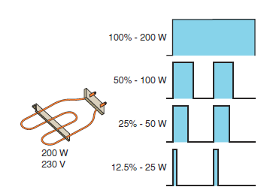
Joonis 4.33 Impulsi laiuse modulatsioon

Sellist sees väljas suhte muutmist nimetatakse impulsi laiuse modulatsiooniks (PWM inglise keeles).

4.4 KONTROLLERI VALIMINE

Selleks, et lahendada mingi konkreetne protsessi reguleerimise ülesanne, tuleb analüüsida protsessi ja selle alusel valida kontroller.

Milline kontroller valida, sõltub järgmistest teguritest:

kas protsess on integraalse või proportsionaalse toimega (kas isereguleeruv või mitteisereguleeruv);
kui suur on protsessi ajaline viide (aja konstandid või „surnud aeg”);
kui kiiresti tuleb kõrvaldada protsessi väärtuse kõrvalekalded;
kas staatiline viga on aktsepteeritav.

Milliseid kontrollereid millal kasutada?

P kontrollerit võib kasutada lihtsalt juhitavate protsesside korral, kui staatiline viga on lubatav.

PD kontrollereid kasutatakse pika hilistumisajaga protsesside reguleerimisel, kus on lubatav staatiline viga.

I kontrollerid sobivad kasutamiseks protsesside puhul, kui on madalad nõudmised protsessi dünaamika suhtes ja viivitused on väikesed. Staatilist viga ei tohi olla.

PI kontrollerid ühendavad P ja I kontrolleri head omadused. Sellel kontrolleril on hea dünaamiline tunnusjoon ja ta ei tekita staatilist viga. Enamikku protsesse saab juhtida PI kontrolleriga. Aga kui toime aeg peab olema maksimaalne, siis tuleb kasutada PID kontrollerit.

PID kontroller sobib praktiliselt igale protsessile. Võrreldes PI kontrolleriga on ta kiiretoimelisem.

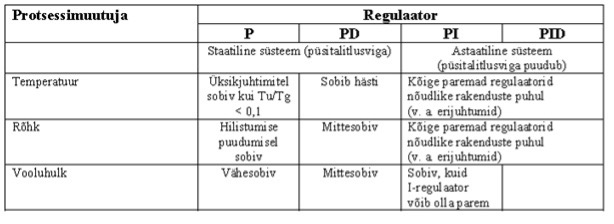
Sõltuvalt reguleeritavast parameetrist võib regulaatori valida järgmiset tabelist:

5. ARS KÄITUMINE SULETUD AHELAS

Siiani me vaatasime juhtimissüsteemi üksikuid koostisosasid (protsessi ja juhtimisseadet) eraldi. Kuidas käitub süsteem tervikuna siis kui suletud ahel on ühendatud? Tuleb uurida süsteemi käitumise stabiilsust ning süsteemi reageerimist seadesuuruse muutustele ja toimet häiringute korral.

Kui kontroller on ühendatud protsessiga, siis me eeldame protsessi muutuja käitumist viisil nagu on kujutatud Joonisel 5.1:

– pärast seda kui juhtimisahel on suletud, peab protsessi muutuja x liikuma seadesuuruse w suunas nii kiiresti kui võimalik ja ilma märkimisväärse ülereguleesimiseta;

– pärast seadesuuruse väärtuseni jõudmist peab protsessi muutuja x säilitama stabiilset väärtust ilma eriliste kõikumisteta;

– häiringute tekkimisel peab kontroller suutma reguleerida väljundsuurust x ilma suurte ülereguleeringuteta suhteliselt lühikese aja jooksul.

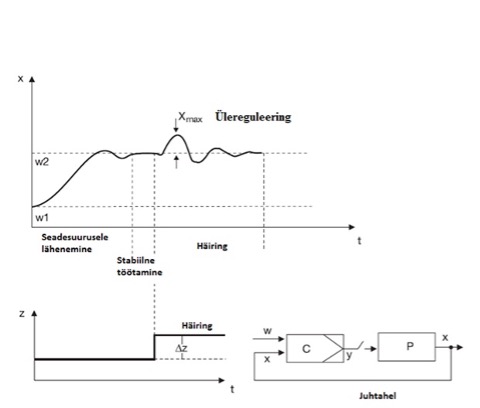
Joonis 5.1 Protsessi muutuja x muutumine suletud juhtimisahelas (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)

5.1 JUHTIMISAHELA STABIILNE JA MITTESTABIILNE KÄITUMINE

Automaatjuhtimissüsteem võib olla stabiilne või mittestabiilne. Süsteem on stabiilne kui siirdeprotsessi järel teatud lõpliku ajavahemiku jooksul taastub automaatjuhtimissüsteemi tasakaaluolek. Seejuures võib stabiilne süsteem tasakaalustuda kas uues olekus, kui kõrvalekalde põhjus säilib, või esialgses olekus, kui kõrvalekalde põhjus möödub. Süsteem on mittestabiilne kui siirdeprotsessi jooksul tasakaaluolek ei taastu. Juhtimisahela stabiilsuse uurimisel tehakse vahet kahe olukorra vahel:

– protsessi muutuja x käitumine ootamatu häiringusignaali tekkimisel;

– protsessi muutuja x käitumise seadesuuruse ootamatu muutumise korral.

5.1.1 SULETUD AHELAGA JUHTIMISE TOIME HÄIRINGUTE KORRAL

Häiringu tekkimisel muutub protsessi väärtus ning reguleerimisahel peab hakkama seda kompenseerima. Teatud aja möödudes protsess kas stabiliseerub (Joonis 5.2) või väljundsuurus hakkab võnkuma (muutub ebastabiilseks).

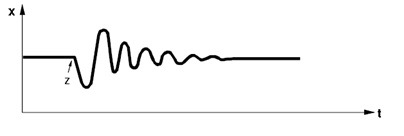
Joonis 5.2 Stabiilne protsess (sumbuva võnkumisega) (Control technology,Siemens)

Ebastabiilse protsessi korral võib rääkida kahest erinevast võnkumise tüübist:

– sumbumatu perioodiline võnkumine;

– kasvava amplituudiga võnkumine.

Sumbumatu perioodilise võnkumise korral (Joonis 5.3) võnkumiste amplituud ja periood omandavad mingi konstantse väärtuse.

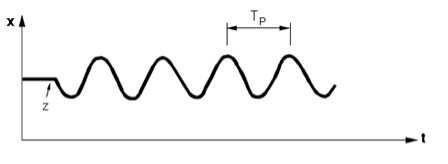
Joonis 5.3 Sumbumatu võnkumisega protsess (Control technology,Siemens)

Püsivalt kasvava amplituudiga võnkumise korral amplituud suureneb ühtlaselt pidevalt, selline protsess ei ole juhitav (Joonis 5.4).

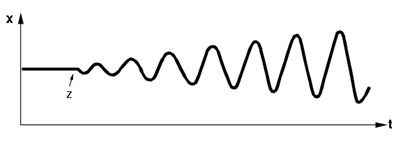
Joonis 5.4 Kasvava amplituudiga võnkuv protsess (Control technology,Siemens)

5.1.2 SULETUD AHELAGA JUHTIMISE TOIME SEADESUURUSE MUUTUMISELE

Juhtimisahela ülesanne on kompenseerida seadesuuruse muutumine kiiresti ja ilma võnkumisteta. Selle nõudmise täitmine sõltub protsessist. On näiteks protsesse, kus väikene ülereguleerimine on lubatud, paljudes protsessides on see aga keelatud. Protsesside toime seadesuuruse hüppelisele muutusele võib olla väga erinev (Joonis 5.5).

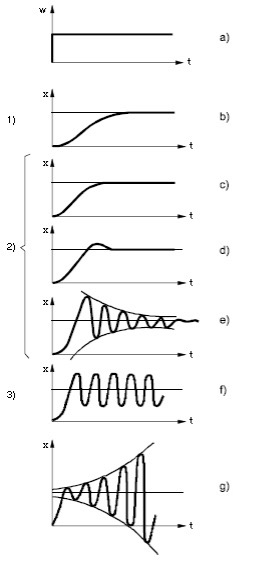
Joonis 5.5 Erinevad toimed seadesuuruse järsu muutuse korral (Control technology,Siemens)

seadesuuruse hüppeline muutumine
ülikriitiliselt summutatud aeglane tõus ilma ülereguleerimiseta
kriitiliselt aeglane, minimaalse võimaliku siirdeajaga, ilma ülereguleerimiseta
vähemkriilise tõusu ja ühe ülereguleeringuga
perioodiliselt sumbuvate ülereguleerimisvõngetaga
perioodilise sumbumatu võnkumisega
perioodilise kasvava amplituudiga võnkumisega

Number 1 kujutab liiga aeglaseid protsesse, number 2 kujutab kasutatavaid variante, number 3 on stabiilsuse piir.

Optimaalseks peetakse Joonisel 5.6 toodud reguleerimisahela toimet seadesuuruse kiirele muutusele:

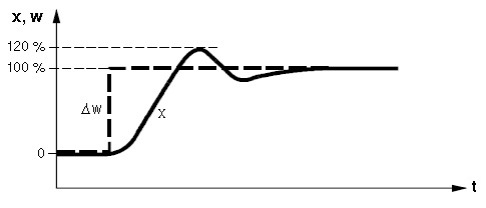
Joonis 5.6 Optimaalne toime seadesuuruse järsule muutumisele. (Control technology,Siemens)

6 SIIRDEPROTSESSI KVALITEET

Automaatreguleerimissüsteem on stabiilne kui siirdeprotsess sumbub teatud aja jooksul. Stabiilse süsteemi kohta ei saa aga alati öelda, et see on ka kvaliteetne. Kvaliteetseks peetakse reguleerimissüsteemi mis on stabiilne ja vastab teatud nõudmistele (Joonis 6.1).

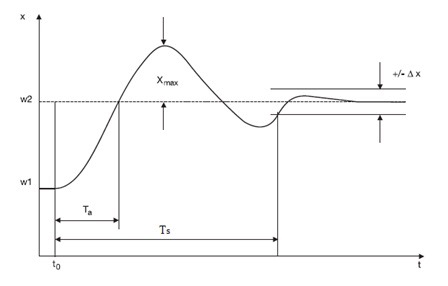
Joonis 6.1 Siirdeprotsessi kvaliteedinäitajad (Control technology,Siemens)

Protsessi väärtus peab saavutama seadesuuruse väärtuse nii kiiresti kui võimalik ja võnkuma nii vähe kui võimalik.

Kvaliteeti iseloomustatakse järgmiste näitajatega:

staatiline viga;
esifrondi kestus $Ta$ ;
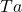tolerants $Δx$ ;
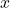siirdeprotsessi kestus $Ts$ ;
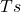maksimaalne ülereguleerimine $xmax$ ;
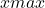võnkuvus.

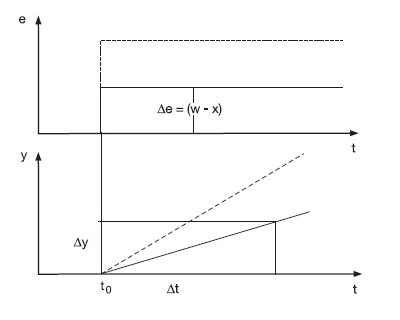
Staatiline viga iseloomustab süsteemi täpsust ja ta on süsteemi siirdeprotsessijärgse väljundsuuruse x ja etteandeväärtuse vahe.

Esifrondi kestuseks Ta nimetatakse ajavahemikku mille jooksul väljundsuurus x saavutab esimest korda soovitud väärtuse.

Tolerantsiks Δx nimetatakse maksimaalset lubatud kõrvalekallet juhttoimega määratud püsiolekust.

Siirdeprotsessi kestuseks Ts nimetatakse ajavahemikku, mille järel siirdeprotsess on kahanenud tolerantsi piiridesse.

Maksimaalne ülereguleerimine xmax määrab ära siirdeprotsessi maksimaalse lubatud amplituudi, mis määratakse süsteemi tööspetsiifikast lähtudes.

Võnkuvus on poollainete arv siirdeprotsessi jooksul

Ideaaljuhul peaks esifrondi kestus Ta olema minimaalne ja ülereguleerimine xmax olema null. Tavaliselt on nende kahe parameetri vahel pöördvõrdeline seos: lühendades esifrondi kestust suureneb ülereguleerimise amplituud ja vastupidi. Kvaliteedi kriteeriumid on seotud protsessiga. Näiteks kiiruse reguleerimisel on tähtis lühike siirdeprotsessi aeg Ts ning väike ülereguleerimine on aktsepteeritav. Samas aga näiteks teatud plastikute tootmise puhul ei ole lubatud temperatuuri ülereguleerumine, sest see võib kahjustada toodangut ja ka seadmeid.

Kõige lihtsam viis siirdeprotsessi kvaliteedinäitajate määramiseks on eksperimentaalne meetod.

Lähme sammhaaval läbi PID-kontrolleri õpetamise ülesande koos põhjalike seletustega. Esitame selle loogiliselt ja praktiliselt, et üliõpilased mõistaksid PID-kontrolleri tööpõhimõtteid ja rakendamist.

PID-kontrolleri õpetamise ülesanne

Eesmärk:

Selgitada PID-kontrolleri tööpõhimõtet, demonstreerida selle mõju süsteemi väljundile ning anda praktiline harjutus, kus üliõpilased saavad reguleerimisparameetreid kohandada ja analüüsida.

1. Sissejuhatus PID-kontrollerisse

PID-kontroller (Proportsionaalne-Integratiivne-Diferentsiaalne kontroller) on automaatjuhtimissüsteemides kasutatav reguleerimisalgoritm, mis aitab hoida protsessi soovitud väärtusel.

PID-kontroller koosneb kolmest komponendist:

P (Proportsionaalne) – reageerib vea suurusele.
I (Integratiivne) – akumuleerib vea aja jooksul ja vähendab püsivat viga.
D (Diferentsiaalne) – reageerib vea muutumiskiirusele, aidates vähendada ülereguleerimist ja võnkumist.

Matemaatiline väljend:

PID-kontrolleri väljund on määratud järgmise valemiga:

$u(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{d e(t)}{dt}$

kus:

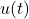$u(t)$ on kontrolleri väljund
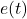$e(t)$ on viga (soovitud ja tegeliku väärtuse vahe)
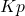$Kp$ on proportsionaalkordaja
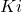$Ki$ on integraalkordaja
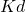$Kd$ on diferentsiaalkordaja

2. Ülesande kirjeldus

Loo lihtne PID-kontroller, mis reguleerib süsteemi väljundit soovitud väärtusele. Kasutame simuleeritud süsteemi, näiteks temperatuuri, mootori kiirust või veetaset.

Simulatsioonikeskkond:

Matlab/Simulink
Python (NumPy + Matplotlib)
PLC (näiteks Siemens TIA Portal või CODESYS)

Ülesande etapid:

Määra süsteemi mudel (nt 1. järku süsteem).
Rakenda PID-kontroller.
Katseta erinevaid parameetreid (Kp,Ki,Kd).
Analüüsi vastust (stabiilsus, ülereguleerimine, ajakonstant).
Optimeeri parameetrid.

3. PID-kontrolleri praktiline rakendamine Pythonis

Kirjutame lihtsa PID-kontrolleri, mis reguleerib simuleeritud süsteemi (nt temperatuuri).

Samm 1: Algseadistused

Importime vajalikud moodulid ja defineerime süsteemi.

import numpy as np
import matplotlib.pyplot as plt

# PID parameetrid
Kp = 1.0  # Proportsionaalne kordaja
Ki = 0.1  # Integraalkordaja
Kd = 0.05  # Diferentsiaalkordaja

# Simulatsiooni parameetrid
dt = 0.1  # Ajasamm
t_end = 10  # Simulatsiooni kestus sekundites
time = np.arange(0, t_end, dt)

# Algväärtused
setpoint = 10  # Soovitud väärtus (näiteks temperatuur 10°C)
process_variable = 0  # Algväärtus (näiteks esialgne temperatuur)
integral = 0
previous_error = 0
output = []

# PID-kontrolleri arvutus
for t in time:
    error = setpoint - process_variable
    integral += error * dt
    derivative = (error - previous_error) / dt
    control_signal = Kp * error + Ki * integral + Kd * derivative
    process_variable += control_signal * dt  # Simuleeritud süsteemi dünaamika
    
    output.append(process_variable)
    previous_error = error

# Tulemuste kuvamine
plt.plot(time, output, label="Protsessi muutuja")
plt.axhline(setpoint, color='r', linestyle='--', label="Soovitud väärtus")
plt.xlabel("Aeg (s)")
plt.ylabel("Väljund")
plt.legend()
plt.grid()
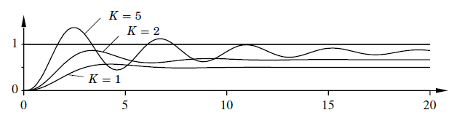
plt.show()

4. PID-parameetrite mõju analüüs

Muutkem PID-parameetreid ja vaatleme nende mõju süsteemi reageerimisele.

Mõju analüüs:

Kp (proportsionaalne):
- Suurendab reageerimiskiirust.
- Liiga suur Kp tekitab võnkumisi ja ülereguleerimist.
Ki (integraal):
- Eemaldab püsivea.
- Liiga suur Ki võib põhjustada süsteemi ebastabiilsust.
Kd (diferentsiaalne):
- Aitab vähendada võnkumist.
- Liiga suur Kd muudab süsteemi tundlikuks müra suhtes.

Harjutus üliõpilastele:

Muutke PID-parameetreid ja joonistage uued graafikud.
Leidke optimaalsed Kp,Ki,Kd väärtused süsteemi stabiliseerimiseks.
Kirjeldage, kuidas erinevad parameetrid mõjutavad süsteemi käitumist.

5. Praktiline ülesanne PLC jaoks

Ülesande kirjeldus:

Looge PLC programmis PID-plokk.
Seadistage andurid ja ajamid, mis annavad süsteemi tagasisidet.
Kalibreerige PID-kontroller, muutes parameetreid.
Testige, kuidas süsteem reageerib häiretele ja muutustele.

Küsimused üliõpilastele:

Milline parameeter mõjutab süsteemi reageerimiskiirust?
Kuidas leida PID-parameetrite parimad väärtused?
Kuidas mõjutavad PID-seaded erinevaid juhtimissüsteeme (nt temperatuur, rõhk, mootori kiirus)?

6. Kokkuvõte

PID-kontroller on laialt kasutatav automaatjuhtimise algoritm.
Selle seadistamine nõuab mõistmist, kuidas Kp,Ki ja Kd mõjutavad süsteemi.
Praktiline testimine ja simulatsioonid aitavad leida optimaalsed parameetrid.
PID-kontrollerit kasutatakse tööstuses laialdaselt, alates masinate juhtimisest kuni keemiliste protsesside optimeerimiseni.