Sissejuhatus juhtimisse
1 AUTOMAATJUHTIMISE SÜSTEEM
Iga automaatjuhtimise süsteem (Joonis 1) koosneb kahest põhilisest elemendist:
a) protsess;
b) kontroller.
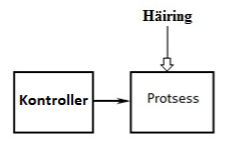
Joonis 1 AJS üldistatud struktuurskeem
Protsessiks võib olla seade, masin, masinate kogum või tehnoloogiline protsess mida soovitakse juhtida. Protsess on juhtimissüsteemi alus, mille ümber ehitatakse süsteem.
Automaatjuhtimissüsteemi keskuseks võib pidada juhtseadet. Kontrolleri ülesandeks on mõjutada protsessi nii, et saavutatakse nõutud väljundtulemus.
Häiring on ebasoodne väline mõju protsessi parameetritele.
Protsessi käitumist mõjutavad juhtseadme poolt antav juhttoime ja häiringud.
2 DISKREETSED PROTSESSID JA NENDE AUTOMAATJUHTIMINE
Eristatakse diskreetseid ja pidevaid protsesse. Diskreetsete protsesside korral juhitakse protsessi sammude toimumise järjekorda.
2.1 Diskreetsed protsessid
Diskreetsete protsesside tööoperatsioone ja seisundit saab määratleda „sees” – „väljas” olekutega (Joonis 2.1):
– kas mootor on sisselülitatud või väljalülitatud;
– ventiil on suletud või avatud;
– mahuti on täis või tühi;
– kas lõppasend on saavutatud või ei ole.

Joonis 2.1 Diskreetne protsess
Diskreetsete protsesside tööoperatsioone saab käsitleda koosnevana üksikutest sammudest. Diskreetse protsessi näideteks on espresso kohvimasin (Joonis 3.2) .

Joonis 2.2 Espresso kohvimasin
Sellisel kohvimasinaga saab valmistada erinevat kohvi. Iga erineva reziimi jaoks on kohvi valmistamise protsessi sammude (kohvipuru doseerimine, koore lisamine, suhkru lisamine jne.) kindel järjekord. Kogu protsess toimub „avatud”-„suletud” reziimis.
2.2 DISKREETSETE PROTSESSIDE JUHTIMINE
Diskreetsete protsesside juhtimist võib jagada kaheks (Joonis 2.3):
Joonis 2.3 diskreetsete protsesside juhtimine
2.2.1 LOOGILINE JUHTIMINE
Loogilise juhtimise korral juhtseadme väljundsignaal sõltub igal hetkel ainult sisendsignaalidest. Sellise juhtimise toime ei sõltu ajast. Juhtimissüsteem ei sisalda ka mäluelemente. Juhtimisahela põhilisteks elementideks on loogikaelemendid AND, OR, NOT ja lisaelementideks NAND ja NOR (Joonis 2.4).
Joonis 2.4 põhilised loogikaelemendid
Põhiliselt kasutatakse loogilise juhtimise põhimõtet automaatkaitse, automaatse signalisatsiooni ja automaatblokeeringu ahelates. Need ahelad peavad otsekohe rakenduma vastava loogikakombinatsiooni tekkimisel juhtprogrammis, et kaitsta seadmel töötavaid inimesi, ümbritsevat keskkonda või seadet ennast avariiolukordades.
2.2.2 JÄRJENDJUHTIMINE
Järjendjuhtimise korral toimuvad protsessi tööoperatsioonid kindla järjekorra alusel. Ühe tööoperatsiooni lõppemine annab stardi signaali järgmise algamiseks. Järjendjuhtimise näideteks on (Joonis 2.5):
– pesumasin;
– valgusfoor;
– lift.
Joonis 2.5 Valgusfoor ja pesumasin
Järjendjuhtimise võib omakorda jagada kaheks (Joonis 3.6):
Joonis 2.6 Järjendjuhtimise jagunemine
2.2.2.1 SÜNKROONNE JÄRJENDJUHTIMINE
Sünkroonse järjendjuhtimise korral toimuvad kõik tööoperatsioonid etteantud aja möödudes. Selline juhtimise süsteemi töö ei sõltu ühestki välisest sündmusest. Põhimõtteliselt ta ei vajaks juhtimiseks ühtegi andurit. Keskkütte taimerid (Joonis 2.7) teostavad sünkroonset juhtimist. Kellaajad, millal küte sisse või välja lülitada on kindlaks määratud.
Joonis 2.7 Keskkütte taimer
Sünkroonset juhtimist nimetatakse ka ajaliseks juhtimiseks.
2.2.2.2 ASÜNKROONNE JÄRJENDJUHTIMINE
Asünkroonse järjendjuhtimise korral toimuvad tööoperatsioonid kas välise sündmuse mõjul või eelmise tööoperatsiooni lõppemise järel. Asünkroonset juhtimist kasutatakse seal, kus aeg ei oma protsessi töös tähtsust. Iga järgnev tööoperatsioon algab täpselt siis, kui eelmine on lõppenud või kui midagi juhtub väljaspool süsteemi. Sellised süsteemid vajavad andureid, et tuvastada eelmise tööoperatsiooni lõppemist või välise sündmuse toimumist.
Hoone lifti juhitakse asünkroonselt (Joonis 2.8). Tööoperatsioonide järjestus sõltub täielikult välistest sündmustest (inimesed vajutavad lifti kutsumise nuppu väljastpoolt ja korruse nuppu lifti sees), või lifti liikumise lõppemisest (lift lõpetab liikumise kui ta on jõudnud vajalikule korrusele ja avab uksed).
Joonis 2.8 Lift
Reaalsete diskreetsete protsesside juhtimine on tavaliselt segu sünkroonsest ja asünkroonsest juhtimisest:
– kaasaegsed valgusfoorid omavad tihti ka jalakäijate tulesid ja andureid autode olemasolu kontrollimiseks. See muudab muidu nende sünkroonse (puhtalt ajalise) juhtimise asünkroonseks (tulede ümberlülitamine sõltub nüüd ka jalakäijate juhuslikest nupule vajutustest ja autode olemasolust ristmikul);
– lifti automaatuksed jäävad korrusele jõudes kindlaks ajaks avatuks. See muudab muidu täielikult asünkroonse juhtimissüsteemi segasüsteemiks.
https://www.youtube.com/watch?v=QCh0g4wPRkQ mobiilide koostamine
3 PIDEVAD PROTSESSID JA NENDE JUHTIMINE
3.1 PIDEVAD PROTSESSID
Pidevad protsessid on sellised protsessid, mis nõuavad protsessi parameetrite pidevat jälgimist ja juhtimist eesmärgiga hoida need etteantud piirides.
Kõige levinumad protsessi parameetrid on temperatuur, voolu hulk, rõhk ja tasapind.
Eriti suurt tähtsust omavad parameetrite väärtused tänapäeval tootmises. Selleks, et toodang oleks kvaliteetne ja konkurentsivõimeline, tuleb väga täpselt pidada kinni protsessi etteantud parameetrite väärtustest. Iga kõrvalekalle võib tekitada tõsiseid kvaliteedi probleeme.
Protsessist (tema karakteristikutest) lähtuvalt peab juhtseade genereerima juhttoime, et tagada protsessi eesmärgipärane käitumine.
Edaspidi kasutame protsesside iseloomustamiseks kahte graafilist karakteristikut:
– dünaamilist karakteristikut (e. hüppekaja);
– staatilist karakteristikut.
Nende karateristikute abil on kõige lihtsam selgitada automaatjuhtimissüsteemi elementide kui ka süsteemi kui terviku tööd.
3.1.1 PIDEVA PROTSESSI DÜNAAMILINE AJAKARAKTERISTIK
Üheks tähtsaks protsessi iseloomustavaks näitajaks on dünaamiline karakteristik e. hüppekaja. See näitab väljundsuuruse ajalist muutumist sisendsuuruse hüppelisel muutumisel.
Dünaamiline karakteristik iseloomustab siirdeprotsessi e. väljundsignaali ajalist muutumist. Sellist karakteristikut nimetatakse ka siirdekarakteristikuks.
Ajakarakteristikute saamiseks antakse protsessi sisendisse tavaliselt ühikhüppe signaal.
Ühikhüpe on sisendsuuruse astmeline muutumine (Joonis 3.1).
Joonis 3.1 Ühikhüpe (Raul Naadal, Automaatjuhtimise alused, 2006)
Ühikhüppele vastavat väljundsignaali nimetatakse ka hüppekajaks (Joonis 3.2).
Joonis 3.2 Hüppekaja (Raul Naadal, Automaatjuhtimise alused,2006)
Hüppekaja on kõige levinum automaatreguleerimissüsteemide dünaamiline karakteristik.
Hüppekajast lähtuvalt klassifitseeritakse protsesse järgmiselt:
– P protsessid (proportsionaalne juhtimise toime);
– I protsessid (integraalne juhtimise toime);
– „surnud ajaga” protsessid;
– energiat salvestavate elementidega protsessid (esimest, teist, jne järku ).
Tuleb vahet teha protsesside vahel, millised saavutavad uue tasakaalu oleku peale sisendsuuruse muutumist ja millised ei saavuta seda:
– isereguleeruvad protsessid saavutavad uue tasakaalu olukorra sisendsignaali muutumise korral;
– mitte isereguleeruvad protsessid ei saavuta uut tasakaalu olukorda. Nende väljundsignaal hakkab pidevalt kasvama või kahanema sisendsignaali hüppelisel muutumisel.
3.1.1.1 P PROTSESSI DÜNAAMILINE KARAKTERISTIK
P protsess reageerib praktiliselt ilma viivituseta sisendsignaali muutustele. Sisuliselt P protsessi dünaamiline karakteristik kordab sisendsignaali karakteristikut, ta on sama kujuga. Seda illustreerib Joonisel 3.3 toodud vooluhulga reguleerimise süsteem. Juhtimise elemendiks on lineaarse tunnusjoonega käsitsi reguleeritav ventiil 1.Vooluhulka mõõdetakse mõõteriistaga 3. Ajahetkel T0 avatakse hüppeliselt ventiili Δy = 4 mm = 40 %, samaaegselt tekkib väljundis vooluhulga hüppeline tõus Δx=2 m3/h.
Joonis 3.3 P protsessi dünaamiline karakteristik (Control technology,Siemens)
Absoluutselt ilma väljundsignaali hilinemiseta (salvestuseta) protsesse tegelikult ei eksisteeri. Igasuguse energia ülekandmine võtab alati teatud aja. Seega väljundsignaali väike hilistumine eksisteerib reaalselt alati.
3.1.1.2 I PROTSESSI DÜNAAMILINE KARAKTERISTIK
I protsessid on mitte isereguleeruvad. Kui tema sisendsuurus muutub, siis väljundsuurus ei stabiliseeru vaid hakkab lineaarselt kasvama või kahanema.
Vee taseme reguleerimise süsteem kujutab endast tüüpilist mitte isereguleeruvat protsessi (Joonis 3.4). Sisendmuutujaks on vee sissevoolu hulk anumasse v (l/h) ja väljundmuutujaks on veepinna tase anumas h (m). Väljundmuutuja on konstantne 1 m juures siis kui vee sissevool ja vee väljavool on võrdsed.
Joonis 3.4 Vee taseme juhtimise süsteem (Control technology,Siemens)
Kui ajahetkel T0 suureneb sissevoolu hulk väärtuselt 400 l/h väärtuseni 500 l/h (sisse voolab rohkem vett kui välja), hakkab vee tasapind lineaarselt tõusma ning mingi aja möödudes anum hakkab üle voolama. Eeldades, et sissevoolu suurenemisel 100 l/h võrra tõuseb vee tase anumas 0,2 m/h, siis mahuti täitub 15 tunni pärast:
Juhul kui mitte isereguleeruva protsessi sisendmuutuja muutub Δv võrra, siis väljundmuutuja h hakkab liikuma kõrvale eelmisest väärtusest saavutamata uut tasakaaluolukorda. Väljundmuutuja muutumise kiirus on proportsionaalne sisendmuutja muutusega. Mitte isereguleeruvad süsteemid vajavad reguleerimiseks kindlasti suletud ahelaga juhtimissüsteemi.
3.1.1.3 „SURNUD AJAGA” PROTSESSI DÜNAAMILINE KARAKTERISTIK
„Surnud ajaga” protsessid reageerivad sisendsignaali muutusele alles teatud aja Tt möödumisel. Tüüpiliseks näiteks on lintkonveier (Joonis 3.5).
Joonis 3.5 „Surnud ajaga” protsess (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Kui juhitava seadme asend muutub nii, et konveieri lindil puisteaine kihi kõrgus suureneb, siis andur tuvastab selle alles teatud aja pärast. Samamoodi käituvad ka pikad gaasitorud. Kulub teatud aeg, enne kui gaasi rõhk jõuab pika turu lõppu. Probleemi leevendab anduri lähemale toomine (kui see on tehniliselt võimalik). „Surnud aeg” põhjustab juhtimise seisukohalt alati suuri probleeme.
3.1.1.4 ÜHE SALVESTAVA ELEMENDIGA PROTSESSI DÜNAAMILINE KARAKTERISTIK
Iga juhitav objekt sisaldab tavaliselt komponente mis on võimelised salvestama energiat. Näiteks mingi ruumi küttesüsteemis on nendeks: boiler, vesi, radiaator, õhk, ruumi seinad jne. Erineva salvestavate elementide arvuga protsessid omavad erinevat dünaamilist tunnusjoont. Salvestavad elemendid põhjustavad väljundsignaalide hilistumist.
Ühe energiat salvestava elemendiga juhtimise objekti aitab selgitada Joonisel 3.6 kujutatud elektriliselt köetav vee anum.
Joonis 3.6 Ühe salvestuselemendiga protsess (Control technology,Siemens)
Anumas olev segisti 3 tagab vee temperatuuri ühtlase jaotumise kogu anuma ulatuses. Ainsaks märkimisväärseks salvestavaks elemendiks süsteemis võib pidada vett. Kütteelemendi ja anuma korpuse salvestavat mõju võib lugeda tühiseks. Sisendmuutujaks y on kütteelemendi lüliti asend ja väljundmuutujaks on vee temperatuur, mida mõõdetakse termomeetriga 4. Kui lüliti 1 on sisse lülitamata, siis olgu vee temperatuur x1= 20°C. Kui ajahetkel T0 sulgeda lüliti siis hakkab vee temperatuur praktiliselt momentaalselt tõusma. Algul on vee temperatuuri tõus suhteliselt kiire, muutudes aga hiljem järjest aeglasemaks kuni lõpuks saavutab väärtuse 50°C. Vee temperatuuri tõusmise aeg sõltub anuma mahust. Väiksema mahuga anumas soojeneb vesi sama küttevõimsuse juures kiiremini ja vastupidi. Temperatuuri muutumise tunnusjoon kujutab eksponentfunktsiooni. Antud tunnusjoont iseloomustatakse ajalise karakteristikuga TS, mis on määratud protsessi energia salvestamise mahuga ja ülekandeteguriga KS. Ajakonstant Ts on aeg, mis kuluks lõpptemperatuuri (antud juhul 50°C) saavutamiseks temperatuuri tõusu kiirusega v (vaata eelmist joonis), mis tekkis vahetult peale kütte sisselülitamist.
Praktiliselt ühe energiat salvestava elemendiga protsesside puhul tõuseb väljundsuurus 63.2 % ajakonstandi Ts jooksul. Viiekordse Ts möödudes saavutab väljundsuurus 99,3% lõppväärtusest (Joonis 3.7). Mida suurem on objekti ajakonstant Ts, seda aeglasemalt muutub väljundsuurus y.
Joonis 3.7 Ühe energiat salvestava elemendiga protsessi ajaline muutumine
Ühe energiat salvestava elemendiga protsessi nimetatakse ka esimest järku süsteemiks.
3.1.1.5 KAHE VÕI ENAMA SALVESTAVA ELEMENDIGA PROTSESSI DÜNAAMILINE KARAKTERISTIK
Kui ühendada järjestikku kaks või enam ühe salvestava elemendiga protsessi, siis saame teist või enamat järku süsteemi.
Joonisel 3.8 on esimeseks salvestavaks elemendiks kuumutusvarras, mis on küllaltki massiivne ja teiseks salvestavaks elemendiks on vesi.
Joonis 3.8 Kahe salvestava elemendiga protsess
Siin on järjestikku ühendatud kaks ühe salvestava elemendiga objekti (Joonis 3.9):
Joonis 3.9 Kahe ühe salvestava elemendiga objekti järjestikune ühendamine
Näiteks kui ühendame kaks mahutit järjestikku (Joonis 3.10):
Joonis 3.10 Kahe mahuti järjestikune ühendamine
Kõrgemat (kahe või enama salvestava elemendiga) järku süsteemi tunnusjoonel on käändepunkt (Joonis 3.11). Kuni käändepunktini tõuseb dünaamiline tunnusjoon, peale seda hakkab aga langema.
Joonis 3.11 Kõrgemat järku juhitava objekti dünaamiline tunnusjoon (Control technology,Siemens)
Kõrgemat järku süsteeme iseloomustatakse kahe ajakonstandiga mis defineeritakse käändepunkti kaudu:
-Tu protsessi hilinemise aeg;
-Tg protsessi reageerimise aeg.
Erineva salvestavate elementide arvuga (teist või kõrgemat järku süsteemide) protsesside dünaamilised tunnusjooned on toodud Joonisel 3.12.
Joonis 3.12 Kõrgemat järku süsteemide dünaamilised karakteristikud (Control technology,Siemens)
Reaalsed protsessid koosnevad erinevate karakteristikutega üksikprotsesside jadast (Joonis 3.13):
Joonis 3.13 Protsesside jada
Mida rohkem salvestavaid elemente (s.t. mida kõrgemat järku süsteem on) protsess sisaldab, seda pikemaks läheb viivituse aeg Tu ja seda raskem on objekti reguleerida.
3.1.2 ISEREGULEERUVA PROTSESSI STAATILINE KARAKTERISTIK
Juhtimise objekti käitumise iseloomustamise tähtsaks karakteristikuks on ka staatiline karakteristik.
Isereguleeruvate protsesside korral väljundmuutuja x omandab alati uue stabiilse väärtuse sõltuvalt sisendmuutuja muutuse väärtusest Δy. Tekib uus tasakaalu olukord (isereguleerumine). Isereguleeruva protsessi näiteks on ruumi kütmine reguleeritava elektriradiaatoriga (Joonis 3.14). Kui keerata radiaatori regulaator asendist 1 asendisse 3, siis ruumi temperatuur ei hakka tõusma lõpmatult, vaid ta saavutab uue kõrgema (x3) taseme teatud aja möödudes. Kui reguleerimise lülitit keerata aga ainult ühe astme võrra, siis temperatuur stabiliseerub natuke madalamal väärtusel (x2).
Joonis 3.14 Elektriliselt köetav ruum (Control technology,Siemens)
Protsessi staatiline karakteristik kujutab väljundmuutuja x ja sisendmuutuja y vahelist seost tasakaaluolukorras (siis kui siirdeprotsessid on lõppenud). Sisendmuutuja y muutus (regulaatori lülitamine asendist 1 asendisse 3) tekitab väljundmuutuja x muutuse (ruumi temperatuur tõuse 18°C-lt 22°C-ni). Muutuse suurust iseloomustab ülekandetegur KS:
Seega ülekandetegur näitab mitu korda muutub väljundmuutuja sisendmuutuja ühe ühiku kohta.
Joonisel 3.14 toodud elektriliselt köetava ruumi ülekandetegur on:
Sisendsuuruse muutumisel 0%-lt kuni 100 %-ni (köetava ruumi näites regulaatori keeramisel asendist „0″ asendisse „3″) st. sisendsuuruse reguleerimise ulatuses Yh, saame väljundsuuruse muutumise ulatuse Xh(Joonis 3.15) ehk reguleerimise ulatuse.
Joonis 3.15 Ruumi temperatuuri reguleerimise ulatus (Control technology,Siemens)
Reguleerimise ulatus on protsessi tähtis parameeter. Ta näitab kui palju muutub väljundsuurus kui sisendsuurus muutub kogu võimalikus ulatuses Yh. Meie ruumi kütmise näites Joonisel 26 on reguleerimise ulatus Xh= 6°C.
Isereguleeruvas protsessis on igale spetsiifilisele sisendmuutuja väärtusele vastav väljundmuutuja väärtus. Sellist seost saab väljendada graafiliselt ühendades vastavad punktid. Niimoodi moodustub juhitava süsteemi staatiline karakteristik.
Lineaarse staatilise karakteristikuga protsesse leidub vähe. Joonisel 3.16 näeme radiaatoriga köetava ruumi staatilist karakteristikut. Sisendsuuruseks on ventiili asend y, mille abil reguleeritakse konstantse temperatuuriga küttevee sissevoolu radiaatorisse (lineaarselt sõltuvalt ventiili asendist). Väljundsuuruseks on ruumi temperatuur x. Tunnusjoon ei ole lineaarne. Ventiili asendi muutus Δy1 vahemikus 0….20 % tekitab ruumi temperatuuri muutuse Δ x1 temperatuurist 14 °C kuni temperatuurini 19 °C, seega 5 °C. Aga ventiili asendi muutus Δy2 vahemikus 40….60 % tekitab ruumi temperatuuri muutuse Δx2= 1,4°C. Ülekandetegur ei ole konstantne: tunnusjoone algusosas on sees suurem ja lõpuosas märgatavalt väiksem.
Joonis 3.16 Radiaatoriga köetava ruumi staatiline tunnusjoon (Control technology,Siemens)
3.1.3 ISEREGULEERUVATE PROTSESSIDE JUHITAVUS
Komplekset juhtimise objekti võib alati käsitleda koosnevana erineva dünaamilise karakteristikuga (P, I, „surnud aeg” ja salvestavate elementidega) juhtimisobjektide kooslusena, mille resulteeriv karakteristik on koostisosade karakteristikute kombinatsioon. Integraalse karakteristikuga juhtimisobjektide puudumisel võib komplekse juhtimisobjekti juhitavust hinnata hilistumise aja Tu ja reageerimise aja Tg väärtuste põhjal. Aegu Tu ja Tg saab määrata graafiliselt teostades reaalsed mõõtmised. Erinevate sisendsuuruste väärtuste juures saadakse vastavad väljundsuuruste väärtused (Joonis 3.17). Saadud karakteristikult määratakse aegade Tu ja Tg väärtused. Nende aegade suhe annab informatsiooni objekti juhitavuse kohta:
– Tg/Tu rohkem kui 10: objekt on kergesti juhitav;
– Tg/Tu 10 ja 3 vahel: objekti saab juhtida;
– Tg/Tu vähem kui 3: objekti on raske juhtida.
Juunis 3.17 Aegade Tu ja Tg määramine (Control technology,Siemens)
Mida rohkem juhtimise objekt sisaldab salvestavaid elemente, seda pikemaks läheb hilistumise aeg Tu (Joonis 3.18) s.t. seda hiljem väljundsignaal muutub.
Joonis 3.18 0….6 identse salvestava elemendiga juhitava objekti ajad Tu ja Tg (Control technology,Siemens)
3.2 PIDEVATE PROTSESSIDE JUHTIMINE
Protsessist (tema karakteristikutest) lähtuvalt peab juhtseade genereerima juhttoime, et tagada protsessi eesmärgipärane käitumine.
Informatsiooni liikumise suuna alusel jaotatakse automaatjuhtimissüsteemid kaheks:
– avatud ahelaga AJS;
– suletud ahelaga AJS.
3.2.1 AVATUD AHELAGA AJS JUHTIMINE
Avatud ahelaga AJS-s toimub info liikumine ainult ühes suunas: juhtseadmelt juhtimisobjekti poole (Joonis 3.19). Juhtseadme juhttoime ei sõltu juhtimisobjekti olekust.
Joonis 3.19 Informatsiooni liikumine avatud ahelaga AJS-s
Avatud ahelaga protsessi juhtimise näitena vaatleme ahju, mille temperatuuri on vaja hoida konstantsel väärtusel (Joonis 3.20).
Joonis 3.20 Ahju temperatuuri avatud ahelaga juhtimine (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Eeldades, et välised tingimused (häiringud) ei muutu, siis igale võimsuse regulaatori asendile vastab alati kindel ahju temperatuur. Nõutud ahju temperatuur saavutatakse võimsuse regulaatori teatud kindlasse asendisse viimisel.
Aga kui välistingimused siiski muutuvad, siis ahju temperatuur hakkab erinema soovitud väärtusest. Välistingimuste muutusteks võivad olla ahju ümbritseva temperatuuri muutumine, kütteelemendi toitepinge muutumine või ka ahju ukse unustamine lahtisesse asendisse. Kõik need välised muutused (häiringud) toovad kaasa ahju temperatuuri muutumise, kuigi võimsuse regulaator on asendis, mis peaks tagama temperatuuri nõutud (etteantud) väärtuse.
Avatud ahelaga juhtimine on olemuselt lihtne, kuid reaalsetes tingimustes (häiringute olemasolul) ta ei suuda hoida juhitavat parameetrit (antud näites ahju temperatuuri) etteantud väärtusel.
https://www.youtube.com/watch?v=FurC2unHeXI avatud ahelaga juhtimine
3.2.2 SULETUD AHELAGA AJS JUHTIMINE
Suletud ahelaga AJS-s toimub info liikumine kahes suunas (Joonis 3.21). Juhtseade saab informatsiooni juhtimisobjekti oleku kohta. Süsteem on tagasisidega. Juhtseade töötleb tagasiside signaali teatud algoritmi alusel. Suletud ahelaga AJS juhttoime sõltub väljundi olekust.
Joonis 3.21 Informatsiooni liikumine suletud ahelaga süsteemis
Vaatame uuesti ahju näidet. Selleks, et ahju temperatuur püsiks etteantud väärtusel ka välistingimuste (häiringute) muutumise korral, tuleb kasutada suletud ahelaga juhtimissüsteemi (Joonis 3.22 ).
Joonis 3.22 Ahju temperatuuri suletud ahelaga juhtimine (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Suletud ahelaga süsteemide suureks eeliseks on nende võime kompenseerida kõikvõimalikke häiringuid, mis paratamatult tekivad kõikides juhtimissüsteemides. Selliseid süsteeme nimetatakse ka automaatreguleerimise süsteemideks (ARS-ks). Juhtimise eesmärgist lähtuvalt võib ARS-e jagada kolmeks:
– stabiliseerimise ARS: väljundsuurust hoitakse stabiilselt etteantud väärtusel (Joonis 3.23);
Joonis 3.23 Stabiliseerimise ARS (Control technology,Siemens), kus
W- seadesuurus
x – protsessi väärtus
y – juhttoime
– programmeeritavad ARS-d: väljundsuurus muutub ajaliselt kindla etteantud seaduspära alusel (Joonis 3.24);
Joonis 3.24 Programmeeritav ARS (Control technology,Siemens)
– järgivad ARS-d: väljundsuurus muutub tundmatu (määramatu, juhusliku) seaduspärasuse järgi (Joonis 3.25).
Allpool toodud joonisel on temperatuuri reguleerimise süsteemi seadesuuruseks välisõhu temperatuur.
Joonis 3.25 Järgiv ARS (Control technology,Siemens)
Automaatreguleerimine on automaatjuhtimine, mille puhul füüsikalis-tehnoloogiliste protsesside parameetreid hoitakse juhtseadme abil jäävatena (stabiliseeriv reguleerimine) või muudetakse selle abil soovitud viisil (programm- ja järgivreguleerimine).
https://www.youtube.com/watch?v=5NVjIIi9fkY&index=3&list=PLn8PRpmsu08q8CE0pbZ-cSrMm_WYJfVGd suletud ahelaga juhtimine
Automaatreguleerimise süsteemi võib kujutada järgmisel joonisel toodud skeemina (Joonis 3.26)
Joonis 3.26 Automaatreguleerimise süsteem
https://www.youtube.com/watch?v=u1pgaJHiiew&index=4&list=PLn8PRpmsu08q8CE0pbZ-cSrMm_WYJfVGdautomaatreguleerimisdsüsteemi elemendid
Näiteid suletud ahelaga juhtimisest:
Joonis 3.27 Söömise reguleerimine
Joonis 3.28 Auto teel hoidmine
3.2.3 AUTOMAATREGULEERIMISAHELA PARAMEETRID
Suletud ahelaga juhtimissüsteemis esinevad järgmised parameetrid (Joonis 3.29):
Joonis 3.29 Suletud ahelaga juhtimissüsteemi parameetrid
– protsessi muutuja x: protsessi muutujat püütakse hoida etteantud väärtusel või muuta seda mingi seaduspärasuse alusel. Tema väärtust mõõdetakse ja tulemus edastatakse kontrollerile;
– seadesuurus w: määratud väärtus mille protsessi muutuja x peab saavutama (näiteks soovitud ahju temperatuur eelnevates näidetes). Seda parameetrit ei mõjuta kontrolleri juhtimistoime, see antakse ette juhtimisahelast väljastpoolt;
– veasignaal e: veasignaal on seadesuuruse ja protsessi muutuja väärtuse vahe: e = w – x;
– häiring z: häiring on protsessile avalduv väline mõju, millega kaasneb protsessi muutuja soovimatu ja ettearvamatu muutumine. Häiringute tõttu on vaja reguleerimiseks kasutada suletud ahelaga juhtimissüsteemi;
– juhttoime y: muutuja mille kaudu protsessi väärtust mõjutatakse soovitud viisil. Ta on protsessi sisendmuutuja. Õige juhttoime määramine on suletud ahelaga juhtimissüsteemis väga tähtis. Juhttoime genereerib kontroller.
4 KONTROLLER
Kontrolleri ülesandeks automaatreguleerimise süsteemis on mõjutada protsessi niimoodi, et protsessi väärtus x vastaks seadesuurusele w. Kontroller koosneb võrdluselemendist ja võimendist (Joonis 4.1).
Joonis 4.1 Kontrolleri ehitus (Controllers and Controlled Systems, Samson AG,1999)
Võrdluselement kalkuleerib veasignaali e etteandesuuruse w ja protsessi muutuja x vahena. Võimendi genereerib veasignaalist e juhttoime signaali y.
Sõltuvalt kontrolleri väljundsignaali tüübist võib juhttoime olla pidev või katkeline (Joonis 4.2).
Joonis 4.2 Kontrollerite klassifitseerimine (Controllers and Controlled Systems, Samson AG,1999)
Pidevattoimelise kontrolleri väljundsignaal (juhttoime y) võib omada mistahes väärtust kontrolleri väljundsignaali diapasooni ulatuses. Pidevatoimelise kontrolleri tunnusjoon kujutab tavaliselt proportsionaalset (P), integraalset (I) või diferentsiaalset (D) toimet või nende toimete kombinatsiooni.
Katketoimelise kontrolleri väljundsignaal muutub diskreetsete suurustena. Tehakse vahet kahepositsiooniliste, kolmepositsiooniliste ja multipositsiooniliste kontrollerite vahel.
4.1 KATKELISE TOIMEGA KONTROLLERID
Pidevatoimelise kontrolleri väljundsuurus võib omada mistahes väärtust vahemikus y0 kuni ymax. Katkelise toimega kontrollerite väljundsignaalid omavad ainult teatud diskreetseid väärtusi.
4.1.1. KAHEPOSITSIOONILINE KONTROLLER
Lihtsaim katkelise toimega kontroller on kahepositsiooniline kontroller, mille väljund võib omada ainult kahte väärtust: 0 või ymax. Tüüpiliseks näiteks on elektrilise triikraua temperatuuri reguleerimine bimetallist lülituselemendi abil ( Joonis 4.3).
Joonis 4.3 Temperatuuri juhtimine bibetallist lüliti abil (Controllers and Controlled Systems, Samson AG,1999)
Bimetall on antud juhul nii mõõte- kui ka lülituselement. Kui lülitada triikraud sisse, siis toimub kuumutusplaadi soojendamine läbi bimetallist lüliti. Teatud temperatuuri juures paindub bimetallist lüliti ülemine metall rohkem kui alumine, mille tulemusel vooluahel katkeb. Temperatuuri alanedes sulgub kontakt uuesti.
Kahetoimelise kontrolleri lülituskarakteristik on toodud Joonisel 4.4.
Joonis 4.4 Kahetoimelise kontrolleri lülituskarakteristik (Control technology,Siemens)
Ülaltoodud karakteristiku korral lülitub kontrolleri väljund y välja x = w juures. Juhul, kui tekib minimaalne kõrvalekalle seadesuurusest, lülitub y uuesti sisse. Sellise karakteristiku juures võib toimuda liiga sage väljundi ümberlülitumine, mis võib kahjustada kontrolleri väljundelementi. Selle vältimiseks muudetakse lülituskarakteristikut nii, et sisse- ja väljalülituse punktid viiakse üksteisest eemale Xsd võrra e. tekitatakse hüsterees (Joonis 4.5). Sellega väheneb ümberlülituste sagedus märgatavalt, kuid tekib protsessi väärtuse x perioodiline võnkumine hüstereesi laiuse ulatuses.
Joonis 4.5 Kahetoimelise kontrolleri hüstereesiga lülituskarakteristik (Control technology,Siemens)
Järgneval joonisel on kujutatud kütmise suletud ahelaga juhtimist (Joonis 4.6):
Joonis 4.6 Temperatuuri katkeline juhtimine
Tüüpiline esimest järku protsessi juhtiva kahetoimelise kontrolleri juhtimistsükli näide on toodud Joonisel 4.7.
Joonis 4.7 Kahepositsioonilise kontrolleri juhtimistsükkel (Controllers and Controlled Systems, Samson AG,1999)
Lülitussagedus sõltub protsessi parameetrist Ts ja hüstereesi suurusest. Kui Ts väheneb, siis suureneb ümberlülituste sagedus. Seega lühikese ajakonstandiga protsesside reguleerimiseks ei ole kahepositsiooniline kontroller sobiv.
Kõrgemat järku protsesside korral tekib ülereguleerimine (Joonis 4.8). Seadesuuruse saavutamisel lülitub väljund ümber, kuid protsessi väärtus kasvab veel teatud suuruseni aja Tu jooksul. Sama toimub ka sisselülitamise punktis. Kahetoimelist kontrollerit kasutatakse lihtsate protsesside juhtimiseks, kus nõuded protsessi parameetri stabiilsusele on väikesed.
Joonis 4.8 Kahepositsiooniline kontroller kõrgemat järku protsessis (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Kahepositsiooniline juhtimine on odav kuid mitte piisavali täpne enamike tööstuslike protsesside jaoks. Enamasti kaasneb kahepositsioonilise reguleerimisega ülereguleerimine. Väljundparameeter võngub pidevalt seadesuuruse ümber.
4.1.2. KOLMEPOSITSIOONILINE KONTROLLER
Kahepositsioonilise kontrolleri puuduseks on see, et temaga ei ole võimalik juhtida reversiivseid protsesse või etapiviisilist lülitust. Kolmepositsiooniline kontroller on kombinatsioon kahest kahepositsioonilisest kontrollerist. Kolmepositsioonilisel kontrolleril on kolm väljundsignaali taset. Temperatuuri juhtimise süsteemis oleks väljundsignaalideks „küte sees”, „küte väljas” ja „jahutus sees” (Joonis 4.9).
Joonis 4.9 Kolmepositsioonilise kontrolleri lülituskarakteristik (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Kolmepositsioonilise kontrolleri abil saab vähendada väljundsignaali võnkuvat käitumist, sest ta pakub lisaks „sees” või „väljas” signaalidele (kahepositsioonilise kontrolleri puhul) veel vahepealset väljundsignaali, mis asub väljundsignaali diapasooni keskpunktis (joonis 4.10).
Joonis 4.10 Kolmeastmelise kontrolleri väljundsignaal (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)
Kui seadesuurus on saavutatud, siis kontrolleri väljundsignaal jääb 50% -liseks maksimaalsest väljundsignaalist ymax. Näitena vaatame temperatuuri reguleerimist seadesuurusega w = 50̊ C (joonis 4.11).
Joonis 4.11 Temperatuuri reguleerimine kolmeastmelise kontrolleriga (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)
Kui temperatuur jääb 40̊ C ja 60̊ C vahele, siis on kütteelement lülitatud sisse 50% -lise võimsusega. Temperatuuri tõustes üle 60̊ C lülitatakse küttevõimsus välja ning temperatuuri langemisel alla 40̊ C lülitatakse küte 100%-liselt sisse.
Multipositsioonilise kontrolleri puhul on väljundsignaalide tasemeid rohkem kui kolm (Joonis 4.12).
Joonis 4.12 Multipositsioonilise kontrolleri lülituskarakteristik (Controllers. Theory and implementation, L. A. Bryan, E. A. Bryan, 1997)
Kolme ja enampositsioonilisi kontrollereid kohtab praktikas harva, sest pole eriti palju mitmepositsioonilise juhtimisega täiturelemente.
4.2 PIDEVATOIMELISED KONTROLLERID
Enamiku protsesside juhtimiseks kasutatakse pidevatoimelist kontrollerit. Pidevatoimeline kontroller saadab analoogsignaali täiturelemendile, millega mõjutatakse protsessi väärtust nii, et veasignaal muutub suletud ahelaga juhtimise korral nulliks.
Joonis 4.13 Pidevatoimeline kontroller
4.2.1 P KONTROLLER
P kontrolleri väljundsignaal y ( protsessi juhttoime) on proportsionaalne (võrdeline) veasignaaliga e. P kontroller reageerib veasignaali e muutusele ilma viivituseta. P kontrolleri väljundsignaal tekib ainult veasignaali e olemasolul. Kui veasignaal puudub (st. protsessi muutuja väärtus on täpselt võrdne etteantud väärtusega w), siis p kontrolleri väljundsignaal puudub (on võrdne nulliga).
P kontrolleri dünaamiline karakteristik on kujutatud Joonisel 4.14.
Joonis 4.14 P kontrolleri dünaamiline tunnusjoon (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
P kontrolleri väljundsuurus y on määratud proportsionaalse toime koefitsendiga KP:
y = KP *e
See on lineaarne sõltuvus ( Joonis 4.15). Mida suurem on proportsionaalse toime koefitsendi KP väärtus seda suurem on graafiku tõusunurk ja seega ka väljundsuurus y.
Joonis 4.15 Väljundsuuruse y sõltuvus koefitsendist KP (Controllers and Controlled Systems, Samson AG,1999)
P kontrolleriga suletud juhtimisahelas tekib alati häiringute või seadesuuruse muutumise korral protsessi muutuja staatiline viga.
Kontroller püüab kompenseerida häiringust tingitud protsessi muutuja x muutumise genereerides juhttoime signaali, mis toimib häiringust toimunud x muutusele vastupidises suunas. Kuna P kontroller tekitab juhttoime ainult kõrvalekalde olemasolul, siis permanentset muutust, mida nimetatakse staatiliseks veaks, pole P kontroller võimeline kompenseerida (Joonis 4.16).
Joonis 4.16 Staatiline viga P kontrolleri korral (Controllers and Controlled Systems, Samson
AG,1999)
Joonis 4.17 Staatilise vea tekkimine häiringu korral.
Häiringu korral toimub järgmine protsess (Joonis 4.17):
- kui ventiil B avaneb, hakkab vedelik mahutist välja voolama ja tema nivoo langeb;
- vedeliku nivoo langemine toob kaasa ujuki madalamale laskumise, mis omakorda tekitab ventiili A avanemise ja vedeliku sissevoolamise paaki;
- selline protsess kestab seni kuni ujuk on avanud ventiili A niivõrd, et vedeliku sissevool paaki võrdsustub vedeliku väljavooluga paagist;
- staatilise vea tõttu stabiliseerub vedeliku tase uuel väärtusel, mis aga erineb etteandeväärtusest.
Joonis 4.18
Joonis 4.19
Staatilise vea suurus sõltub P kontrolleri koefitsiendist KP. Mida suurem on KP, seda väiksem on staatiline viga.
P kontrolleri tingmärk skeemidel:
P kontrollerid on kiiretoimelised. Neid võib kasutada seal, kus ei esitata väga rangeid nõudmisi reguleerimisprotsessile ja kus on lubatav staatilise vea tekkimine.
P kontrolleri kasutamise eelised:
– P kontroller on kiiretoimeline;
– õigesti valitud KP korral väga stabiilne reguleerimisprotsess.
P kontrolleri kasutamise puudused:
– häiringute toimel staatilise vea tekkimine.
4.2.2 I KONTROLLER
Integraalset kontrollerit kasutatakse selleks, et täielikult kõrvaldada kõrvalekalle mistahes reguleerimispunktis. Niikaua kui kõrvalekalle ei ole null, põhjustab integraalne toime juhttoime muutuse. Kontrolleri väljundsuurus muutub proportsionaalselt veasignaali integraalile (Joonis 4.20):
Kui kiiresti suureneb/väheneb juhttoime y, see sõltub vea suurusest ja integreerimise ajast Tn. Kui integreerimise aeg on lühike, siis kontrolleri väljundsignaal muutub kiiresti ja vastupidi.
Joonis 4.20 I kontrolleri dünaamiline karakteristik (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
Joonis 4.21
Mida suurem on e ja mida suurem on Ki, seda suurem on kontrolleri väljundsignaal.
I kontrolleri puhul muutub sama suure veasignaali korral väljundsignaal y palju aeglasemalt kui P kontrolleri puhul. Kui lühendada integreerimise aega, siis y muutus kiireneb, kuid tekib süsteemi võnkumamineku oht.
I kontrolleri tingmärk skeemidel:
I kontrolleri kasutamise eelised:
– I kontroller ei jäta staatilist viga.
I kontrolleri kasutamise puudused:
– suure integreerimise aja korral väljundsignaali y muutus liiga loid;
– lühikese integreerimise aja korral süsteemi võnkumamineku oht (ebastabiilsus).
4.2.3 D KONTROLLER
D (diferentsiaalne ) kontroller genereerib juhttoime y lähtuvalt veasignaali muutumise kiirusest, mitte selle amplituudist. Järelikult D kontroller reageerib palju kiiremini kui P kontroller. Isegi siis, kui veasignaal on väike, genereerib D kontroller suure amplituudiga juhttoime juhul kui veasignaal muutub. Kui veasignaal on konstantne (sõltumata tema suurusest), siis on D kontrolleri väljundsignaal 0. D kontrollerit üksikuna kasutatakse väga harva. Tavaliselt kasutatakse teda koos teiste kontrolleritüüpidega, peamiselt koos P kotrolleriga.
Ideaalse D kontrolleri dünaamiline karakteristik veasignaali järsul muutumisel on toodud Joonisel 4.22.
Joonis 4.22 Ideaalse D kontrolleri dünaamiline karakteristik (Control technology,Siemens)
Ideaalse D kontrolleri väljundis tekib veasignaali hüppelise muutumise korral lõpmatu amplituudiga väga lühiajaline impulss. Peale väljundsignaali y impulsi lõppu muutub väljundsignaal kohe nulliks, kuigi veasignaal jääb kestma.
D kontrolleri iseloomustamiseks sobib palju paremini ühtlaselt muutuva veasignaali muutuse karakteristik, mis näitab väljundsignaali y muutumist erinevate veasignaali muutumise kiiruste muutumise korral (Joonis 7.23).
D kontrolleri korral on väljundsignaali muutumise ulatus ΔyD proportsionaalne vea muutumise kiiruse muutumisega vx. D kontrollerit iseloomustab diferentsiaalse toime koefitsient KD, mis väljendab seost väljundsuuruse muutumise ulatuse ΔyD ja veasignaali kiiruse muutumise kiiruse vahel vx:
KD = ΔyD / vx
Joonis 4.23 D kontrolleri ühtlaselt muutuva veasignaali muutuse tunnusjoon (Control technology,Siemens)
D kontrolleri tingmärk:
4.2.4 PI KONTROLLER
PI kontroller (Joonis 4.24) saadakse siis, kui ühendatakse paralleelselt P ja I kontrollerid. PI kontrolleri dünaamiline karakteristik on P kontrolleri ja I kontrolleri karakteristikute summa (Joonis 4.25).
Joonis 4.24 PI kontroller (Control technology,Siemens)
Joonis 4.25 PI kontrolleri dünaamiline karakteristik (Control technology,Siemens)
P kontroller tekitab esmase väljundsuuruse tõusu ΔyP, mis on võrdeline veasignaaliga e. I kontrolleri toime tõttu hakkab väljundsignaal y kasvama kiirusega, mille määrab ära integreerimise koefitsient KI. Teatud kindla aja möödumisel (t0…t1) koosneb väljundsignaali muutus ΔyPI kahe komponendi summast:
ΔyPI= ΔyP + ΔyI
Kui veasignaal e jääb kestma, siis jätkub väljundsignaali y tõus lõpmatult.
PI kontroller on määratud kahe reguleeritava parameetriga:
– esimene karakteristik on P kontrolleri proportsionaalse toime koefitsient KP;
– teiseks karakteristikuks on integraalse toime aeg Tn, mis tuleneb I kontrolleri tegurist KI.
Tn on aeg mida I kontroller vajab (sama sisendsignaali juures), et tekitada väljundsignaali muutus ΔyI, on mis võrdne P kontrolleri poolt tekitatud väljundsignaali muutusega ΔyP (Joonis 4.26).
Joonis 4.26 Integraaltoime aja Tn definitsioon (Control technology,Siemens)
Puhtalt I kontroller peaks sama sisendsignaali korral aja Tn võrra varem hakkama avaldama toimet, et tekitada väljundsignaali muutus ΔyP, mille tekitab P kontroller.
4.2.5 PD KONTROLLER
PD kontrolleri moodustavad paralleelselt ühendatud P ja D kontroller (Joonis 4.27).
Joonis 4.27 PD kontroller (Control technology,Siemens)
PD kontrolleri dünaamiline karakteristik kujutab endast P kontrolleri ja D kontrolleri karakteristikute summat (Joonis 4.28).
Joonis 4.28 PD kontrolleri dünaamiline karakteristik (Control technology,Siemens)
Tänu D toimele tekitab kontroller veasignaali e astmelisel muutumisel suure väljundsignaali y, mis hakkab ajakonstandiga TD eksponentsiaalselt vähenema kuni nullini. Edasi määrab kontrolleri toime P komponent. PD kontroller suudab veasignaali kompenseerida märksa kiiremini kui aimult P kontroller. Nii nagu P kontroller tekitab ka PD kontroller staatilise vea.
PD kontrolleri kirjeldamiseks sobib paremini ühtlaselt muutuva veasignaali muutuse tunnusjoon (Joonis 4.29).
Joonis 4.29 PD kontrolleri ühtlaselt muutuva veasignaali muutuse tunnusjoon (Control technology, Siemens)
PD kontrollerit iseloomustavad järgmised suurused:
– P kontrolleri proportsionaalse toime koefitsient KP;
– D kontrolleri koefitsient KD või diferentsiaalse toime aeg Tv.
Diferentsiaalse toime aeg Tv näitab kui kaua enne tunnusjoone murdepunkti oleks pidanud algama P kontrolleri toime tõus , et saavutada väljundsignaali tõus ΔYD, mille D kontroller saavutab hetkeliselt.
4.2.6 PID KONTROLLER
PID kontroller kujutab endast P, I ja D kontrolleri paralleelühendust (Joonis 4.30).
Joonis 4.30 PID kontroller (Control technology,Siemens)
PID kontrolleri dünaamiline tunnusjoon: (Joonis 4.31).
Joonis 4.31 PID kontrolleri tunnusjoon (Control technology,Siemens)
PID kontrolleri dünaamiline tunnusjoon kujutab P, I ja D elementide tunnusjoonte summat. Esialgne suur väljundsignaali y tõus on tingitud D elemendist, seejärel tunnusjoon langeb peaaegu P elemendi tunnusjoone tasemeni ja siis hakkab lineaarselt tõusma I elemendi tunnusjoone toimel. I elemendi tõttu kompenseerib PID kontroller seadesuuruse või häiringute poolt tekitatud veeasignaali muutused ja on kiirem kui PI või P kontroller.
PID kontrolleri dünaamiline tunnusjoon on määratud kolme parameetriga:
– P kontrolleri proportsionaalse toime koefitsient KP;
– integraalse toime aeg Tn;
– diferentsiaalse toime aeg Tv.
PID kontrollerit kasutatakse keeruliste süsteemide korral, kus nõutakse kiiret stabiliseerumist ja staatilise vea olemasolu pole lubatud.
4.3 KVASI-PIDEV KONTROLLER
Kvasi-pidev kontroller koosneb pidevast kontrollerist, mille väljundisse on ühendatud lülituselement.
Joonis 4.32 Kvasi-pidev kontroller
Sellise kontrolleri väljundsignaal omab väärtusi 0% või 100% (kas sees või väljas). Sujuvalt muudetakse sees ja väljasoleku aegade suhet. Suhte sujuva muutmisega muudetakse sisuliselt väljundsignaali keskmist väärtust.
Joonis 4.33 Impulsi laiuse modulatsioon
Sellist sees väljas suhte muutmist nimetatakse impulsi laiuse modulatsiooniks (PWM inglise keeles).
4.4 KONTROLLERI VALIMINE
Selleks, et lahendada mingi konkreetne protsessi reguleerimise ülesanne, tuleb analüüsida protsessi ja selle alusel valida kontroller.
Milline kontroller valida, sõltub järgmistest teguritest:
– kas protsess on integraalse või proportsionaalse toimega (kas isereguleeruv või mitteisereguleeruv);
– kui suur on protsessi ajaline viide (aja konstandid või „surnud aeg”);
– kui kiiresti tuleb kõrvaldada protsessi väärtuse kõrvalekalded;
– kas staatiline viga on aktsepteeritav.
Milliseid kontrollereid millal kasutada?
P kontrollerit võib kasutada lihtsalt juhitavate protsesside korral, kui staatiline viga on lubatav.
PD kontrollereid kasutatakse pika hilistumisajaga protsesside reguleerimisel, kus on lubatav staatiline viga.
I kontrollerid sobivad kasutamiseks protsesside puhul, kui on madalad nõudmised protsessi dünaamika suhtes ja viivitused on väikesed. Staatilist viga ei tohi olla.
PI kontrollerid ühendavad P ja I kontrolleri head omadused. Sellel kontrolleril on hea dünaamiline tunnusjoon ja ta ei tekita staatilist viga. Enamikku protsesse saab juhtida PI kontrolleriga. Aga kui toime aeg peab olema maksimaalne, siis tuleb kasutada PID kontrollerit.
PID kontroller sobib praktiliselt igale protsessile. Võrreldes PI kontrolleriga on ta kiiretoimelisem.
Sõltuvalt reguleeritavast parameetrist võib regulaatori valida järgmiset tabelist:
5. ARS KÄITUMINE SULETUD AHELAS
Siiani me vaatasime juhtimissüsteemi üksikuid koostisosasid (protsessi ja juhtimisseadet) eraldi. Kuidas käitub süsteem tervikuna siis kui suletud ahel on ühendatud? Tuleb uurida süsteemi käitumise stabiilsust ning süsteemi reageerimist seadesuuruse muutustele ja toimet häiringute korral.
Kui kontroller on ühendatud protsessiga, siis me eeldame protsessi muutuja käitumist viisil nagu on kujutatud Joonisel 5.1:
– pärast seda kui juhtimisahel on suletud, peab protsessi muutuja x liikuma seadesuuruse w suunas nii kiiresti kui võimalik ja ilma märkimisväärse ülereguleesimiseta;
– pärast seadesuuruse väärtuseni jõudmist peab protsessi muutuja x säilitama stabiilset väärtust ilma eriliste kõikumisteta;
– häiringute tekkimisel peab kontroller suutma reguleerida väljundsuurust x ilma suurte ülereguleeringuteta suhteliselt lühikese aja jooksul.
Joonis 5.1 Protsessi muutuja x muutumine suletud juhtimisahelas (Control Engineering, A guide for beginners, Manfred Schleicher, Frank Blasinger, 2003)
5.1 JUHTIMISAHELA STABIILNE JA MITTESTABIILNE KÄITUMINE
Automaatjuhtimissüsteem võib olla stabiilne või mittestabiilne. Süsteem on stabiilne kui siirdeprotsessi järel teatud lõpliku ajavahemiku jooksul taastub automaatjuhtimissüsteemi tasakaaluolek. Seejuures võib stabiilne süsteem tasakaalustuda kas uues olekus, kui kõrvalekalde põhjus säilib, või esialgses olekus, kui kõrvalekalde põhjus möödub. Süsteem on mittestabiilne kui siirdeprotsessi jooksul tasakaaluolek ei taastu. Juhtimisahela stabiilsuse uurimisel tehakse vahet kahe olukorra vahel:
– protsessi muutuja x käitumine ootamatu häiringusignaali tekkimisel;
– protsessi muutuja x käitumise seadesuuruse ootamatu muutumise korral.
5.1.1 SULETUD AHELAGA JUHTIMISE TOIME HÄIRINGUTE KORRAL
Häiringu tekkimisel muutub protsessi väärtus ning reguleerimisahel peab hakkama seda kompenseerima. Teatud aja möödudes protsess kas stabiliseerub (Joonis 5.2) või väljundsuurus hakkab võnkuma (muutub ebastabiilseks).
Joonis 5.2 Stabiilne protsess (sumbuva võnkumisega) (Control technology,Siemens)
Ebastabiilse protsessi korral võib rääkida kahest erinevast võnkumise tüübist:
– sumbumatu perioodiline võnkumine;
– kasvava amplituudiga võnkumine.
Sumbumatu perioodilise võnkumise korral (Joonis 5.3) võnkumiste amplituud ja periood omandavad mingi konstantse väärtuse.
Joonis 5.3 Sumbumatu võnkumisega protsess (Control technology,Siemens)
Püsivalt kasvava amplituudiga võnkumise korral amplituud suureneb ühtlaselt pidevalt, selline protsess ei ole juhitav (Joonis 5.4).
Joonis 5.4 Kasvava amplituudiga võnkuv protsess (Control technology,Siemens)
5.1.2 SULETUD AHELAGA JUHTIMISE TOIME SEADESUURUSE MUUTUMISELE
Juhtimisahela ülesanne on kompenseerida seadesuuruse muutumine kiiresti ja ilma võnkumisteta. Selle nõudmise täitmine sõltub protsessist. On näiteks protsesse, kus väikene ülereguleerimine on lubatud, paljudes protsessides on see aga keelatud. Protsesside toime seadesuuruse hüppelisele muutusele võib olla väga erinev (Joonis 5.5).
Joonis 5.5 Erinevad toimed seadesuuruse järsu muutuse korral (Control technology,Siemens)
a) seadesuuruse hüppeline muutumine
b) ülikriitiliselt summutatud aeglane tõus ilma ülereguleerimiseta
c) kriitiliselt aeglane, minimaalse võimaliku siirdeajaga, ilma ülereguleerimiseta
d) vähemkriilise tõusu ja ühe ülereguleeringuga
e) perioodiliselt sumbuvate ülereguleerimisvõngetaga
f) perioodilise sumbumatu võnkumisega
g) perioodilise kasvava amplituudiga võnkumisega
Number 1 kujutab liiga aeglaseid protsesse, number 2 kujutab kasutatavaid variante, number 3 on stabiilsuse piir.
Optimaalseks peetakse Joonisel 5.6 toodud reguleerimisahela toimet seadesuuruse kiirele muutusele:
Joonis 5.6 Optimaalne toime seadesuuruse järsule muutumisele. (Control technology,Siemens)
6 SIIRDEPROTSESSI KVALITEET
Automaatreguleerimissüsteem on stabiilne kui siirdeprotsess sumbub teatud aja jooksul. Stabiilse süsteemi kohta ei saa aga alati öelda, et see on ka kvaliteetne. Kvaliteetseks peetakse reguleerimissüsteemi mis on stabiilne ja vastab teatud nõudmistele (Joonis 6.1).
Joonis 6.1 Siirdeprotsessi kvaliteedinäitajad (Control technology,Siemens)
Protsessi väärtus peab saavutama seadesuuruse väärtuse nii kiiresti kui võimalik ja võnkuma nii vähe kui võimalik.
Kvaliteeti iseloomustatakse järgmiste näitajatega:
– staatiline viga;
– esifrondi kestus Ta;
– tolerants Δx;
– siirdeprotsessi kestus Ts;
– maksimaalne ülereguleerimine xmax;
– võnkuvus.
Staatiline viga iseloomustab süsteemi täpsust ja ta on süsteemi siirdeprotsessijärgse väljundsuuruse x ja etteandeväärtuse vahe.
Esifrondi kestuseks Ta nimetatakse ajavahemikku mille jooksul väljundsuurus x saavutab esimest korda soovitud väärtuse.
Tolerantsiks Δx nimetatakse maksimaalset lubatud kõrvalekallet juhttoimega määratud püsiolekust.
Siirdeprotsessi kestuseks Ts nimetatakse ajavahemikku, mille järel siirdeprotsess on kahanenud tolerantsi piiridesse.
Maksimaalne ülereguleerimine xmax määrab ära siirdeprotsessi maksimaalse lubatud amplituudi, mis määratakse süsteemi tööspetsiifikast lähtudes.
Võnkuvus on poollainete arv siirdeprotsessi jooksul
Ideaaljuhul peaks esifrondi kestus Ta olema minimaalne ja ülereguleerimine xmax olema null. Tavaliselt on nende kahe parameetri vahel pöördvõrdeline seos: lühendades esifrondi kestust suureneb ülereguleerimise amplituud ja vastupidi. Kvaliteedi kriteeriumid on seotud protsessiga. Näiteks kiiruse reguleerimisel on tähtis lühike siirdeprotsessi aeg Ts ning väike ülereguleerimine on aktsepteeritav. Samas aga näiteks teatud plastikute tootmise puhul ei ole lubatud temperatuuri ülereguleerumine, sest see võib kahjustada toodangut ja ka seadmeid.
Kõige lihtsam viis siirdeprotsessi kvaliteedinäitajate määramiseks on eksperimentaalne meetod.
